福建省福州十九中2023-2024学年九年级上册数学开学试卷
试卷更新日期:2023-10-20 类型:开学考试
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
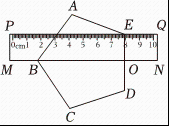
1. 下列各数 , , , , 中,负数的个数有( )A、个 B、个 C、个 D、个2. 2023年政府工作报告提出:确保粮食产量保持在斤以上,将这个数用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 义务教育课程标准年版首次把学生学会炒菜纳入劳动教育课程,并作出明确规定某班有名学生已经学会炒的菜品的种数依次为: , , , , , , 则这组数据的众数和中位数分别是( )A、 , B、 , C、 , D、 ,5. 在下列一次函数中,其图象过点且随的增大而减小的是( )A、 B、 C、 D、6. 据乘用车市场信息联席会数据显示,我国新能源车发展迅速,年月至月,新能源车月销量由万辆增加到万辆,设年月至月新能源车销量的月平均增长率为 , 则可列方程为( )A、 B、 C、 D、7. 关于的一元二次方程有两个不相等的实数根,则的值可能是( )A、 B、 C、 D、8. 如图,将透明直尺叠放在正五边形徽章上,若直尺的下沿于点 , 且经过点 , 上沿经过点 , 则的度数为( )
 A、 B、 C、 D、9. 如图,在▱中,对角线 , 相交于点 , 为的中点,连接 , 过点作于点 , 若 , , 则的长为( )
A、 B、 C、 D、9. 如图,在▱中,对角线 , 相交于点 , 为的中点,连接 , 过点作于点 , 若 , , 则的长为( ) A、 B、 C、 D、10. 已知抛物线经过这两点与 , 若点在抛物线上,则可能的值是( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知抛物线经过这两点与 , 若点在抛物线上,则可能的值是( )A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
11. 若 有意义,则x的取值范围是12. 因式分解: =13. 已知 , 则分式的值为 .14. 如图,直线经过正方形的顶点 , 分别过正方形的顶点、作于点 , 于点 , 若 , , 则的长为 .
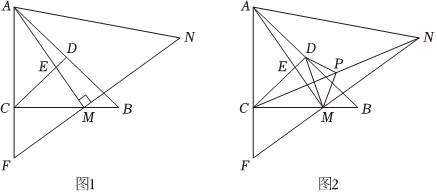
 15. 在现今互联网的时代,密码与我们的生活密不可分数学老师请同学们通过数学知识自己设置五位数密码,现由小明、小亮两位同学轮流从中任选一个数字,规则是小明先选,小明选的数会使这个数据平均数最小,小亮选的数会使这个数据中位数最大,密码的个数据不能重复,若五位数密码第一个数字是 , 要使这个五位数最大,用上述方法产生的密码是 .16. 如图,在等边中,点 , 分别在边和上,连接 , 点关于的对称点是点 , 连接和分别交于点和 , 若 , , 若和四边形面积相等,则的长为 .
15. 在现今互联网的时代,密码与我们的生活密不可分数学老师请同学们通过数学知识自己设置五位数密码,现由小明、小亮两位同学轮流从中任选一个数字,规则是小明先选,小明选的数会使这个数据平均数最小,小亮选的数会使这个数据中位数最大,密码的个数据不能重复,若五位数密码第一个数字是 , 要使这个五位数最大,用上述方法产生的密码是 .16. 如图,在等边中,点 , 分别在边和上,连接 , 点关于的对称点是点 , 连接和分别交于点和 , 若 , , 若和四边形面积相等,则的长为 .
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 解方程:(1)、;(2)、 .18. 如图,已知 , , , 求证: .
 19. 先化简,再求值: , 其中 .20. 如图,在菱形中,为边延长线上一点,连接分别交和于和两点.
19. 先化简,再求值: , 其中 .20. 如图,在菱形中,为边延长线上一点,连接分别交和于和两点. (1)、求证:;(2)、已知 , , 求的长.21. 国家利益高于一切,国家安全人人有责,年月日是第八个全民国家安全教育日,某校开展了“树牢总体国家安全观,感悟新时代国家安全成就”的国安知识竞赛,现从七、八年级中各随机抽取名学生的竞赛成绩分制进行整理、描述和分析成绩用表示,共分成四组:不合格 , 合格 , 良好 , 优秀 , 下面给出部分信息:
(1)、求证:;(2)、已知 , , 求的长.21. 国家利益高于一切,国家安全人人有责,年月日是第八个全民国家安全教育日,某校开展了“树牢总体国家安全观,感悟新时代国家安全成就”的国安知识竞赛,现从七、八年级中各随机抽取名学生的竞赛成绩分制进行整理、描述和分析成绩用表示,共分成四组:不合格 , 合格 , 良好 , 优秀 , 下面给出部分信息:七年级抽取的学生竞赛成绩在良好组的数据是: , , , , , .
八年级抽取的学生竞赛成绩在良好组的数据是: , , , , , , , .
七、八年级抽取的学生竞赛成绩的统计量
七年级
八年级

根据以上信息,解答下列问题:
(1)、直接写出 , 的值;(2)、根据上述数据,你认为该校七八年级中哪个年级学生对“国安知识”学握较好?请说明理由写出一条理由即可;(3)、该校七、八年级各有人参加此活动,估计参加此活动成绩优秀的学生人数是多少?22. 三坊七巷作为“十大历史文化古街”之一,其悠久的历史吸引了许多游客,景点内的、两种纪念品深受广大游客们的喜爱若买件种纪念品和件种纪念品花费元,买件种纪念品和件种纪念品花费元.(1)、求两种纪念品的单价;(2)、游客决定要购买、两种纪念品共件,设购进种纪念品件,购进这件纪念品所需总费用为元若要求购进种纪念品的数量不超过种纪念品的一半,试问如何购进、两种纪念品使得所需总费用最低,最低的费用是多少元?23. 问题背景:在平面直角坐标系中,任意直线轴,直线上的任意两点的坐标为 , 点的坐标为且满足 , 则可以构成函数 .
问题解决:
(1)、已知点 , , 点在点的上方,若点在函数图象上,求的函数解析式;(2)、已知点 , 点且 , 当时,函数的最大值是 , 求的值.