北师版数学七年级上册周测卷（第三章第4--5节）基础卷

试卷更新日期：2023-10-19 类型：同步测试

进入出卷网下载

一、选择题

1. 化简-(a-b-c+d)的结果是（）

A、a-b-c+d B、-a-b-c+d C、a+b+c-d D、-a+b+c-d

查看试题解析
2. 下列去括号正确的是（）

A、-(2x+5)=-2x+5 B、 $- \frac{1}{2}$ (4x-2)=-2x+2 C、 $\frac{1}{3}$ (6x-3)=2x-1 D、+(3x- 2m)=-3x-2m

查看试题解析
3. 如果 $3 a^{m + 3} b^{4}$ 与 $a^{2} b^{n}$ 是同类项，则 $m n$ 的值为（）

A、4 B、-4 C、8 D、12

查看试题解析
4. 下列各选项中的两个项是同类项的是（）.

A、 $a^{3} b^{2}$ 和 $a^{2} b^{3}$ B、 $- 5 a^{3} b$ 和 $3 b a^{3}$ C、 $3 a b c^{2}$ 和 $3 a^{2} b c$ D、 $2 a$ 和 $a^{2}$

查看试题解析
5. 下列语句错误的是（）

A、数字0也是单项式 B、单项式 $- a$ 的系数与次数都是1 C、 $\frac{1}{2} x y$ 是二次单项式 D、 $5 m^{2} n$ 与 $- 2 n m^{2}$ 是同类项

查看试题解析
6. 下列运算中，正确的是（）

A、 $2 (a - b) = 2 a - 1$ B、 $3 a^{2} b - 2 a^{2} b = a^{2} b$ C、 $a^{2} + a^{2} = a^{4}$ D、 $3 x + 2 y = 5 x y$

查看试题解析
7. 若关于 $x$ ， $y$ 的单项式 $3 x^{5} y^{m}$ 与 $- 2 x^{n} y^{7}$ 的和仍为単项式，则 $m - n$ 的值为（）

A、2 B、5 C、7 D、9

查看试题解析
8. 如图是一个运算程序的示意图，若开始输入x的值为18，则第10次输出的结果为（）

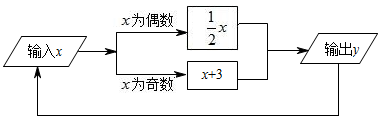A、5 B、0 C、3 D、6

查看试题解析
9. 下列图形都是由面积为1的正方形按一定的规律组成的，其中，第1个图形中面积为1的正方形有9个，第2个图形中面积为1的正方形有14个，……，按此规律，则第（）个图形中面积为1的正方形的个数为2024个．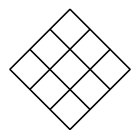

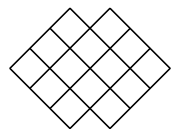
A、402 B、403 C、404 D、405

查看试题解析
10. 探究下列关于x的单项式： $2 x$ ， $- 4 x^{2}$ ， $6 x^{3}$ ， $- 8 x^{4}$ ， $10 x^{5}$ ， …的规律，判断第2021个单项式是（）

A、 $2021 x^{2021}$ B、 $- 2021 x^{2021}$ C、 $4042 x^{2021}$ D、 $- 4042 x^{2021}$

查看试题解析

二、填空题

11. 若 $a^{x - 3} b^{3}$ 与 $- 3 a b^{2 y - 1}$ 是同类项，则 $x^{y} =$

查看试题解析
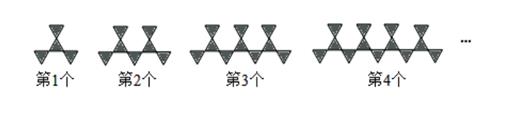
12. 如果一个多项式减去 $2 y^{2} + 3 x^{2}$ 的差等于 $2 x^{2} - y^{2}$ ，那么这个多项式是

查看试题解析
13. 已知关于x，y的多项式 $5 x^{2} y - 2 x y + a x^{2} y + y - 1$ 不含三次项，则a的值为.

查看试题解析
14. 有一串式子：﹣x，2x² ， ﹣3x³ ， 4x⁴ ， …，﹣19x¹⁹ ， 20x²⁰ ， …写出第 2013 个式子，写出第 n 个．

查看试题解析
15. 如图是一组有规律的图案，它们是由边长相等的正三角形组合而成，第1个图案有4个三角形，第2个图案有7个三角形，第3个图案有10个三角形……按此规律摆下去，第n个图案有个三角形(用含n的代数式表示)

查看试题解析
16. 每一个多边形都可分割（分割方法如图）成若干个三角形．根据这种方法八边形可以分割成个三角形．用此方法n边形能割成个三角形．

查看试题解析

三、解答题

17. 化简

(1)、 $(2 x + 5 y) - (3 x - y)$

(2)、 $5 (a^{2} b - 3 a b^{2}) - 2 (a^{2} b - a b^{2} + 1)$

查看试题解析
18. 先化简，再求值：（a²﹣ab﹣7）﹣（﹣4a²+2ab+7），其中a=2，b= $\frac{3}{2}$ ．

查看试题解析
19. 已知 $2 a - b = - 2$ ，求代数式 $3 (2 a b^{2} - 4 a + b) - 2 (3 a b^{2} - 2 a) + b$ 的值.

查看试题解析
20. 若代数式： $(2 x^{2} + a x + y + 6) - (2 b x^{2} - 3 x + 5 y - 1)$ 的值与字母x的取值无关，求代数式 $3 (a^{2} - 2 a b - b^{2}) - (4 a^{2} + a b + b^{2})$ 的值.

查看试题解析
21. 已知 $A = 2 x^{3} - 3 x^{2} + 9$ ， $B = 5 x^{3} - 9 x^{2} - 7 x - 1$ .

(1)、求B-2A:

(2)、当x=-5时，求B-2A的值.

查看试题解析
22. 阅读下列内容，并完成相关问题：
小明说：“我定义了一种新的运算，叫 $*$ (加乘)运算．”然后他写出了一些按照 $*$ (加乘)运算的运算法则进行运算的算式：
(+4)*(+2)＝6；(－4)*(－3)=+7；…
(－5)*(+3)=－8；(+6)*(－7)=－13；…
(+8)*0=8；0*(－9)=9．…
小亮看了这些算式后说：“我知道你定义的 $*$ (加乘)运算的运算法则了．”请你帮助小亮完成下列问题：

(1)、归纳 $*$ (加乘)运算的运算法则：
两数进行 $*$ (加乘)运算，．
特别地， $0$ 和任何数进行 $*$ (加乘)运算，或任何数和 $0$ 进行 $*$ (加乘)运算，都得这个数的绝对值．

(2)、若有理数的运算顺序适合 $*$ (加乘)运算，请直接写出结果：
①(－3) $*$ (－5)= ；
②(+3) $*$ (－5)=；
③(－9) $*$ (+3) $*$ (－6)=；

(3)、试计算：［(－2)*(+3)］*［(－12)*0］(括号的作用与它在有理数运算中的作用一致)；

查看试题解析
23. 观察图，解答下列问题．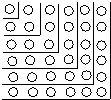

(1)、图中的小圆圈被折线隔开分成六层，第一层有1个小圆圈，第二层有3个圆圈，第三层有5个圆圈，…，第六层有11个圆圈．如果要你继续画下去，那么第八层有几个小圆圈？第n层呢？

(2)、某一层上有65个圆圈，这是第几层？

(3)、数图中的圆圈个数可以有多种不同的方法．
比如：前两层的圆圈个数和为（1+3）或2² ，
由此得，1+3=2² ．
同样，
由前三层的圆圈个数和得：1+3+5=3² ．
由前四层的圆圈个数和得：1+3+5+7=4² ．
由前五层的圆圈个数和得：1+3+5+7+9=5² ．
…
根据上述请你猜测，从1开始的n个连续奇数之和是多少？用公式把它表示出来．

(4)、计算：1+3+5+…+99的和；

(5)、计算：101+103+105+…+199的和．

查看试题解析

北师版数学七年级上册周测卷（第三章 第4--5节） 基础卷

一、选择题

二、填空题

三、解答题

北师版数学七年级上册周测卷（第三章第4--5节）基础卷