河南省郑州市名校2022~2023学年高一下学期期中物理试卷

试卷更新日期：2023-10-19 类型：期中考试

进入出卷网下载

一、单选题（本大题共9小题，共36.0分）

1. 转篮球是一项难度较高的技巧，其中包含了许多物理知识。如图所示，假设某转篮球的高手能让篮球在手指上（手指刚好在篮球的正下方）做匀速圆周运动，下列有关该同学转篮球的物理知识正确的是（）

A、篮球上各点做圆周运动的圆心在手指上 B、篮球上各点的向心力是由手指提供的 C、篮球上各点做圆周运动的角速度相同 D、篮球上各点离转轴越近，做圆周运动的向心加速度越大

查看试题解析
2. 如图所示，小船沿直线AB过河，船头始终垂直于河岸。若水流速度减小，为保持航线不变，下列措施与结论正确的是（）

A、减小船速，过河时间变长 B、减小船速，过河时间不变 C、增大船速，过河时间不变 D、增大船速，过河时间缩短

查看试题解析
3. 如图所示，物体 $A$ 、 $B$ 随水平圆盘绕轴匀速转动，物体 $B$ 在水平方向所受的作用力及其方向的判定正确的有（）

A、圆盘对 $B$ 及 $A$ 对 $B$ 的摩擦力，两力都指向圆心 B、圆盘对 $B$ 的摩擦力指向圆心， $A$ 对 $B$ 的摩擦力背离圆心 C、物体 $B$ 受到圆盘对 $B$ 及 $A$ 对 $B$ 的摩擦力和向心力 D、物体 $B$ 受到圆盘对 $B$ 的摩擦力和向心力

查看试题解析
4. 汽车在地下车库的水平地面上做匀速直线运动，接着驶上一段长直斜坡，最后开上水平路面继续行驶。设全过程中汽车发动机产生的牵引力的功率恒定，汽车在所有路面所受阻力大小不变，则（）

A、汽车开上斜坡上后，立即做匀速直线运动 B、汽车开上水平路面后，立即做匀速直线运动 C、汽车将要离开斜坡时发动机产生的牵引力最大 D、汽车开上水平路面后的速率大于它在地下车库时的速率

查看试题解析
5. 如图所示的传动装置中， $B$ 、 $C$ 两轮固定在一起绕同一轴转动， $A$ 、 $B$ 两轮用皮带传动，三个轮的半径关系是 $r_{A} = r_{C} = 2 r_{B}$ 。若皮带不打滑，则关于 $A$ 、 $B$ 、 $C$ 三轮边缘 $a$ 、 $b$ 、 $c$ 三点的下列物理量的比，错误的是（）

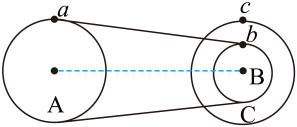A、角速度之比为 $1 ∶ 2 ∶ 2$ B、线速度大小为 $1 ∶ 1 ∶ 2$ C、向心加速度大小之比为 $1 ∶ 2 ∶ 4$ D、周期之比为 $2 ∶ 2 ∶ 1$

查看试题解析
6. 如图所示，质量相同的三颗卫星 $a$ 、 $b$ 、 $c$ 绕地球做匀速圆周运动，其中 $b$ 、 $c$ 在地球的同步轨道上， $a$ 距离地球表面的高度为 $R$ ，此时 $a$ 、 $b$ 恰好相距最近，已知地球质量为 $M$ 、半径为 $R$ 、地球自转的角速度为 $ω$ ，引力常量为 $G$ ，则（）

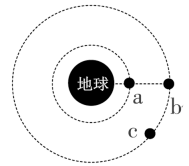A、发射卫星 $b$ 的速度要大于 $11.2 k m / s$ B、卫星 $a$ 的周期大于卫星 $b$ 的周期 C、卫星 $a$ 和卫星 $b$ 下一次相距最近还需经过 $t = \frac{2 π}{\sqrt{\frac{G M}{8 R^{3}}} - ω}$ D、若要卫星 $c$ 与卫星 $b$ 实现对接，可让卫星 $c$ 加速

查看试题解析
7. 如图所示，光滑斜面固定在水平面上，顶端 $O$ 有一小球。小球从静止释放沿斜面运动到底端 $B$ 的时间是 $t_{1}$ 。若给小球一水平初速度，小球恰好落在斜面底端 $B$ ，经过的时间是 $t_{2}$ 。不计空气阻力，则（）

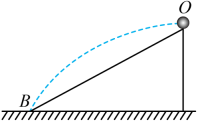A、 $t_{1} < t_{2}$ B、 $t_{2_{}} < t_{1}$ C、 $t_{1} = t_{2}$ D、无法确定

查看试题解析
8. 如图所示，一长为L的轻绳下端拴着质量为m的小球，现使小球在水平面内做匀速圆周运动，轻绳与竖直方向的夹角为θ，重力加速度大小为g，下列说法正确的是（）

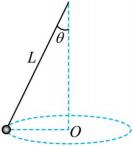A、小球运动的加速度大小为 $\frac{g}{\tan θ}$ B、小球运动的线速度大小为 $\sqrt{g L s i n θ t a n θ}$ C、小球运动的角速度大小为 $\frac{g}{L \tan θ}$ D、轻绳的拉力大小为mgtanθ

查看试题解析
9. 1844年，德国天文学家贝塞尔根据天狼星的移动路径形成的波浪图形，推断天狼星是双星系统中的一颗星。已知天狼星及其伴星都在各自轨道上互相绕转，绕转的周期约为50年，两星体之间的距离约为日地距离的20倍，引力常量为G。则（　　）

A、可估算出双星系统的平均密度 B、可估算出双星系统中任一星体的质量 C、可估算出双星系统的总质量 D、双星系统中质量大的星体离绕行中心远

查看试题解析

二、多选题（本大题共3小题，共12.0分）

10. 如图是“嫦娥三号”飞行轨道示意图。假设“嫦娥三号”运行经过 $P$ 点第一次通过近月制动使“嫦娥三号”在距离月面高度为 $100 k m$ 的圆形轨道Ⅰ上运动，再次经过 $P$ 点时第二次通过近月制动使“嫦娥三号”在距离月面近地点为 $Q$ 、高度为 $15 k m$ ，远地点为 $P$ 、高度为 $100 k m$ 的椭圆轨道Ⅱ上运动，下列说法正确的是（）

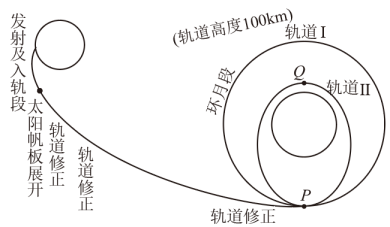A、“嫦娥三号”在距离月面高度为 $100 k m$ 的圆轨道Ⅰ上运动时速度大小可能变化 B、“嫦娥三号”在距离月面高度为 $100 k m$ 的圆轨道Ⅰ上运动的周期一定大于在椭圆轨道Ⅱ上运动的周期 C、“嫦娥三号”在椭圆轨道Ⅱ上运动经过 $Q$ 点时的加速度一定大于经过 $P$ 点时的加速度 D、“嫦娥三号”在椭圆轨道Ⅱ上运动经过 $Q$ 点时的速率可能小于经过 $P$ 点时的速率

查看试题解析
11. 如图所示，一位网球运动员以拍击球，使网球沿水平方向飞出。第一只球飞出时的初速度为 $v_{1}$ ，落在自己一方场地上后，弹跳起来，刚好擦网而过，落在对方场地的 $A$ 点处。第二只球飞出时的初速度为 $v_{2}$ ，直接擦网而过，也落在 $A$ 点处。设球与地面碰撞时没有能量损失，且不计空气阻力，则（）

A、网球两次飞出时的初速度之比 $v_{1} ∶ v_{2} = 1 ∶ 3$ B、网球两次飞出时的初速度之比 $v_{1} ∶ v_{2} = 1 ∶ 2$ C、运动员击球点的高度 $H$ 与网高 $h$ 之比 $H ∶ h = 4 ∶ 3$ D、运动员击球点的高度 $H$ 与网高 $h$ 之比 $H ∶ h = 3 ∶ 2$

查看试题解析
12. 如图所示，水平转台上有一个质量为m的物块，用长为l的轻质细绳将物块连接在转轴上，细绳与竖直转轴的夹角 $θ$ 为 $\frac{π}{6}$ ，此时绳绷直但无张力，物块与转台间动摩擦因数为 $μ = \frac{1}{3}$ ，最大静摩擦力等于滑动摩擦力，物块随转台由静止开始缓慢加速转动，角速度为ω，加速度为g，则（）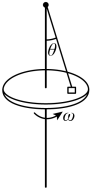

A、当 $ω = \sqrt{\frac{g}{2 l}}$ 时，细线中张力为零 B、当 $ω = \sqrt{\frac{3 g}{4 l}}$ 时，物块与转台间的摩擦力为零 C、当 $ω = \sqrt{\frac{g}{l}}$ 时，细线的张力为 $\frac{m g}{3}$ D、当 $ω = \sqrt{\frac{4 g}{3 l}}$ 时，细绳的拉力大小为 $\frac{4 m g}{3}$

查看试题解析

三、实验题（本大题共2小题，共18.0分）

13. 在“探究向心力 $F_{n}$ 的大小与质量 $m$ 、角速度 $ω$ 和半径 $r$ 之间的关系”的实验中，所用实验器材如图所示。

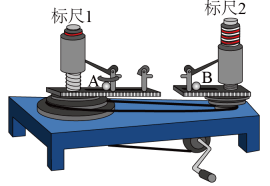(1)、物体所受向心力 $F_{n}$ 的大小与物体的质量 $m$ 、角速度 $ω$ 和圆周运动半径 $r$ 之间的关系是 $F_{n} =$ 。

(2)、某次实验时，选择 $A$ 、 $B$ 两个体积相等的铝球和钢球，变速塔轮相对应的半径之比为 $1$ ： $1$ ，如图所示，是探究哪两个物理量之间的关系____。

A、研究向心力与质量之间的关系 B、研究向心力与角速度之间的关系 C、研究向心力与半径之间的关系 D、研究向心力与线速度之间的关系

(3)、在研究向心力的大小 $F$ 与质量 $m$ 、角速度 $ω$ 和半径 $r$ 之间的关系时，我们主要用到了物理学中的____

A、累积法 B、等效替代法 C、控制变量法 D、微小量放大法

(4)、某次实验保证小球质量和圆周运动半径相等，若标尺上红白相间的等分格显示出两个小球所受向心力的比值为 $1$ ： $4$ ，由圆周运动知识可以判断与皮带连接的变速塔轮相对应的半径之比为____。

A、1：2 B、2：1 C、1：4 D、4：1

查看试题解析
14. 图甲是“研究平抛物体的运动”的实验装置图

(1)、实验前应对实验装置反复调节，直到斜槽末端切线水平，每次让小球从同一位置由静止释放，是为了使每次小球平抛的相同。

(2)、图乙是正确实验取得的数据，其中 $O$ 为抛出点，则此小球做平抛运动的初速度为 $m / s (g$ 取 $9.8 m / s^{2})$ 。

(3)、在“研究平抛运动”的实验中，安装实验装置时，斜槽末端的切线必须水平，这样做的目的是____。

A、保证小球飞出时，速度既不太大，也不太小 B、保证小球飞出时，初速度水平 C、保证小球在空中运动的时间每次都相等 D、保证小球运动的轨迹是一条抛物线

查看试题解析

四、计算题（本大题共4小题，共40.0分）

15. 如图所示，用 $F = 5 N$ 的水平拉力，使物体从 $A$ 点由静止开始沿光滑水平面做加速度为 $1 m / s^{2}$ 的匀加速直线运动到达 $B$ 点，已知 $A$ 到 $B$ 的时间 $t = 4 s$ . 。求：

(1)、 $A$ 、 $B$ 之间的距离；

(2)、拉力 $F$ 在此过程中所做的功；

(3)、求物体从 $A$ 到 $B$ 拉力 $F$ 做功的平均功率。

查看试题解析
16. 发射地球同步卫星时，先将卫星发射到距地面高度为 $h_{1}$ 的近地圆轨道上，在卫星经过 $A$ 点时点火实施变轨进入椭圆轨道，最后在椭圆轨道的远地点 $B$ 点再次点火将卫星送入同步轨道，如图所示．已知同步卫星的运动周期为 $T$ ，地球的半径为 $R$ ，地球表面重力加速度为 $g$ ，忽略地球自转的影响．求：

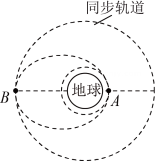(1)、卫星在近地点 $A$ 的加速度大小；

(2)、远地点 $B$ 距地面的高度．

查看试题解析
17. 如图所示，左图是某游乐场中水上过山车的实物图片，右图是其原理示意图．在原理图中半径为 $R = 8.0 m$ 的圆形轨道固定在离水面高 $h = 3.2 m$ 的水平平台上，圆轨道与水平平台相切于 $A$ 点， $A$ 、 $B$ 分别为圆形轨道的最低点和最高点．过山车 $($ 实际是一艘带轮子的气垫小船，可视作质点 $)$ 高速行驶，先后会通过多个圆形轨道，然后从 $A$ 点离开圆轨道而进入光滑的水平轨道 $A C$ ，最后从 $C$ 点水平飞出落入水中，整个过程刺激惊险，受到很多年轻人的喜爱。已知水面宽度为 $s = 12 m$ ，假设运动中不计空气阻力，重力加速度 $g$ 取 $10 m / s^{2} .$ 结果可保留根号．

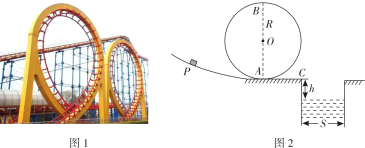(1)、若过山车恰好能通过圆形轨道的最高点 $B$ ，则其在 $B$ 点的速度为多大？

(2)、为使过山车安全落入水中，则过山车在 $C$ 点的最大速度为多少？

(3)、某次运动过程中乘客在圆轨道最低点 $A$ 对座椅的压力为自身重力的 $3$ 倍，则气垫船落入水中时的速度大小是多少？

查看试题解析
18. 如图所示，在水平圆盘上放有质量分别为 $m$ 、 $m$ 、 $2 m$ 的可视为质点的三个物体 $A$ 、 $B$ 、 $C$ ，圆盘可绕垂直圆盘的中心轴 $O O$ 转动。三个物体与圆盘的滑动摩擦因数均为 $μ$ 。最大静摩擦力认为等于滑动摩擦力。三个物体与轴 $O$ 共线且 $O A = O B = B C = r$ ，现将三个物体用轻质细线相连，保持细线伸直且恰无张力，使圆盘从静止开始转动且缓慢增大角速度，直到物体相对圆盘发生滑动，已知重力加速度 $g$ 。则在这个过程中：

(1)、当角速度多大时，物体 $B$ 和物体 $C$ 之间的细绳上恰好开始有张力？

(2)、当角速度多大时，物体 $A$ 和物体 $B$ 之间的细线上恰好开始有张力？

(3)、写出物体 $A$ 所受静摩擦力大小随角速度 $ω$ 变化的函数关系式。

查看试题解析