沪科版数学八年级上册第11,12章平面直角坐标系与一次函数坐标规律探究练习
试卷更新日期:2023-10-19 类型:同步测试
一、选择题
-
1. 如图,在平面直角坐标系中,动点从原点出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得到点;接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点;接着水平向右平移4个单位长度,再竖直向上平移4个单位长度得到点 , …,按此作法进行下去,则点的坐标为( )
 A、 B、 C、 D、2. 如图,在平面直角坐标系中,所有正方形的中心均在坐标原点,且各边与轴或轴平行,从内到外,它们的边长依次为 , , , , , 顶点依次用 , , , , , 表示,则顶点的坐标为( )
A、 B、 C、 D、2. 如图,在平面直角坐标系中,所有正方形的中心均在坐标原点,且各边与轴或轴平行,从内到外,它们的边长依次为 , , , , , 顶点依次用 , , , , , 表示,则顶点的坐标为( )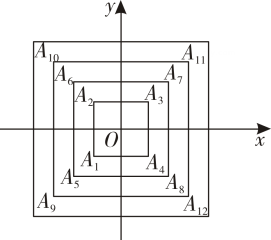 A、 B、 C、 D、3. 如图,平面直角坐标系中,已知点 , , , , 动点从点出发,以每秒个单位的速度按逆时针方向沿四边形的边做环绕运动;另一动点从点出发,以每秒个单位的速度按顺时针方向沿四边形的边做环绕运动,则第次相遇点的坐标是( )
A、 B、 C、 D、3. 如图,平面直角坐标系中,已知点 , , , , 动点从点出发,以每秒个单位的速度按逆时针方向沿四边形的边做环绕运动;另一动点从点出发,以每秒个单位的速度按顺时针方向沿四边形的边做环绕运动,则第次相遇点的坐标是( )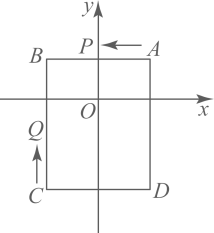 A、 B、 C、 D、4. 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1 , A2B2C2D2 , A3B3C3D3每个正方形四条边上的整点的个数,推算出正方形A10B10C10D10四条边上的整点共有( )个
A、 B、 C、 D、4. 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1 , A2B2C2D2 , A3B3C3D3每个正方形四条边上的整点的个数,推算出正方形A10B10C10D10四条边上的整点共有( )个 A、88 B、84 C、80 D、765. 如图,在平面直角坐标系中,有若干个横坐标,纵坐标均为整数的点,其顺序按图中“→”方向依次排列:根据这个规律,第2023个点的坐标为( )
A、88 B、84 C、80 D、765. 如图,在平面直角坐标系中,有若干个横坐标,纵坐标均为整数的点,其顺序按图中“→”方向依次排列:根据这个规律,第2023个点的坐标为( )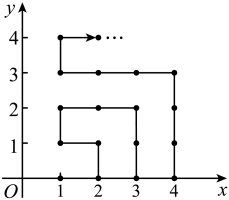 A、 B、 C、 D、6. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0),……,根据这个规律探索可得第2023个点的坐标是( )
A、 B、 C、 D、6. 如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0),……,根据这个规律探索可得第2023个点的坐标是( ) A、 B、 C、 D、7. 如图,动点从坐标原点出发,以每秒一个单位长度的速度按图中箭头所示方向运动,第秒运动到点 , 第秒运动到点 , 第秒运动到点 , 第秒运动到点 , 则第秒时点所在位置的坐标是 .
A、 B、 C、 D、7. 如图,动点从坐标原点出发,以每秒一个单位长度的速度按图中箭头所示方向运动,第秒运动到点 , 第秒运动到点 , 第秒运动到点 , 第秒运动到点 , 则第秒时点所在位置的坐标是 . 8. 如图,在平面直角坐标系中,一动点从原点出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点 , , , , …那么点的坐标为( )
8. 如图,在平面直角坐标系中,一动点从原点出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点 , , , , …那么点的坐标为( ) A、 B、 C、 D、9. 如图,在平面直角坐标系中,动点按图中箭头所示方向从原点出发,第1次运动到点 , 第2次接着运动到点 , 第3次接着运动到点 , 第4次接着运动到点按这样的运动规律,点的坐标是( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,动点按图中箭头所示方向从原点出发,第1次运动到点 , 第2次接着运动到点 , 第3次接着运动到点 , 第4次接着运动到点按这样的运动规律,点的坐标是( ) A、 B、 C、 D、10. 一组按规律排列的式子: , , , , . 第个式子是____(为正整数)( )A、 B、 C、 D、11. 如图,小球起始位置时位于处,沿图中所示的方向击球,小球的运动轨迹如图所示,当小球第次碰到球桌边时,小球的位置是( )
A、 B、 C、 D、10. 一组按规律排列的式子: , , , , . 第个式子是____(为正整数)( )A、 B、 C、 D、11. 如图,小球起始位置时位于处,沿图中所示的方向击球,小球的运动轨迹如图所示,当小球第次碰到球桌边时,小球的位置是( ) A、 B、 C、 D、12. 在平面直角坐标系中,一个智能机器人接到如下指令,从原点O出发,按向右、向上、向右、向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到A1 , 第2次移动到A2 , …,第n次移动到A,则三角形OA2A2022的面积是( )
A、 B、 C、 D、12. 在平面直角坐标系中,一个智能机器人接到如下指令,从原点O出发,按向右、向上、向右、向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到A1 , 第2次移动到A2 , …,第n次移动到A,则三角形OA2A2022的面积是( ) A、505 m2 B、m2 C、m2 D、1011 m213. 正方形 , , , …按如图的方式放置,点 , , , …和点 , , , …分别在直线和轴上,则点的坐标为 .
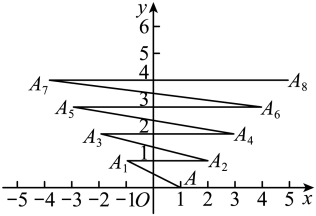
A、505 m2 B、m2 C、m2 D、1011 m213. 正方形 , , , …按如图的方式放置,点 , , , …和点 , , , …分别在直线和轴上,则点的坐标为 . 14. 如图,已知直线: , 直线:和点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线,交直线于点 , 过点作轴的平行线,交直线于点 , 过点作轴的平行线交直线于点 , , 按此作法进行下去,则点的横坐标为( )
14. 如图,已知直线: , 直线:和点 , 过点作轴的平行线交直线于点 , 过点作轴的平行线,交直线于点 , 过点作轴的平行线,交直线于点 , 过点作轴的平行线交直线于点 , , 按此作法进行下去,则点的横坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
15. 如图,动点在平面直角坐标系中按图中箭头所示方向运动,第次从原点运动到点 , 第次接着运动到点 , 第次接着运动到点 , ……,按这样的运动规律,经过第次运动后,动点的坐标是 .
 16. 如图,在平面直角坐标系中,一动点从原点O出发,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0)…,则点P2023的坐标是 .
16. 如图,在平面直角坐标系中,一动点从原点O出发,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0)…,则点P2023的坐标是 .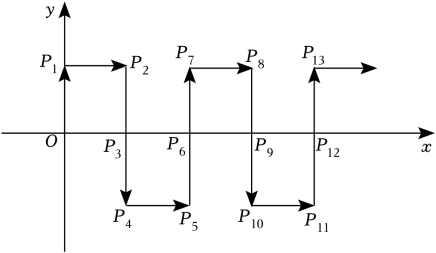 17. 数学家高斯推动了数学科学的发展,被数学界誉为“数学王子”,据传,他在计算时,用到了一种方法,将首尾两个数相加,进而得到 . 人们借助于这样的方法,得到(n是正整数).有下列问题,如图,在平面直角坐标系中的一系列格点 , , 其中 , 2,3, , , , 且 , 是整数.记 , 如 , 即 , , 即 , , 即 , ⋯,以此类推.则 .
17. 数学家高斯推动了数学科学的发展,被数学界誉为“数学王子”,据传,他在计算时,用到了一种方法,将首尾两个数相加,进而得到 . 人们借助于这样的方法,得到(n是正整数).有下列问题,如图,在平面直角坐标系中的一系列格点 , , 其中 , 2,3, , , , 且 , 是整数.记 , 如 , 即 , , 即 , , 即 , ⋯,以此类推.则 .