期中微专题提分精炼2矩形的性质与判定-2023-2024学年北师大版九年级(上)数学
试卷更新日期:2023-10-19 类型:复习试卷
一、选择题
-
1. 矩形、菱形都具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、对角线互相垂直且相等2. 矩形具有而菱形不具有的性质是( )A、两组对边分别平行且相等 B、两组对角分别相等 C、相邻两角互补 D、对角线相等3. 下列测量方案中,能确定四边形门框为矩形的是( )A、测量对角线是否互相平分 B、测量两组对边是否分别相等 C、测量对角线是否相等 D、测量对角线交点到四个顶点的距离是否都相等4. 如图,矩形 的两条对角线相交于点 , , ,则矩形的对角线 的长是( )
 A、2 B、4 C、2 D、45. 如图,在矩形ABCD中,AB=24,BC=12,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形.则AE的长是( )
A、2 B、4 C、2 D、45. 如图,在矩形ABCD中,AB=24,BC=12,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形.则AE的长是( ) A、15 B、20 C、 D、6. ABCD添加下列条件后,仍不能使它成为矩形的是( )A、AB⊥BC B、AC=BD C、∠A=∠B D、BC= CD7. 如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°, , , 若AD=2,则四边形CODE的周长为( )
A、15 B、20 C、 D、6. ABCD添加下列条件后,仍不能使它成为矩形的是( )A、AB⊥BC B、AC=BD C、∠A=∠B D、BC= CD7. 如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°, , , 若AD=2,则四边形CODE的周长为( ) A、12 B、10 C、8 D、48. 如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D同时出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,当四边形ABPQ初次为矩形时,点P和点Q运动的时间为( )秒.
A、12 B、10 C、8 D、48. 如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D同时出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,当四边形ABPQ初次为矩形时,点P和点Q运动的时间为( )秒. A、2 B、3 C、4 D、59. 如图,在矩形中, , 对角线与相交于点O, , 垂足为E, , 则BC的长为( )
A、2 B、3 C、4 D、59. 如图,在矩形中, , 对角线与相交于点O, , 垂足为E, , 则BC的长为( )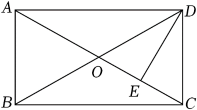 A、 B、6cm C、 D、10. 如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE= AC,连接CE、OE,连接AE交OD于点F,若AB=2,∠ABC=60° , 则AE的长为( )
A、 B、6cm C、 D、10. 如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE= AC,连接CE、OE,连接AE交OD于点F,若AB=2,∠ABC=60° , 则AE的长为( )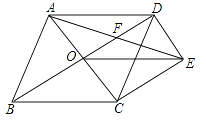 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在矩形 中,对角线 与 相交于点 ,垂足为点 ,且 ,则 的长为.
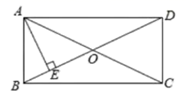 12. 如图,点O是菱形ABCD对角线的交点,DEAC,CEBD,连接OE,设AC=12,BD=16,则OE的长为 .
12. 如图,点O是菱形ABCD对角线的交点,DEAC,CEBD,连接OE,设AC=12,BD=16,则OE的长为 . 13. 如图,在△ABC中,D,E,F分别是AB,BC和AC边的中点,请添加一个条件 , 使四边形BEFD为矩形.(填一个即可)
13. 如图,在△ABC中,D,E,F分别是AB,BC和AC边的中点,请添加一个条件 , 使四边形BEFD为矩形.(填一个即可)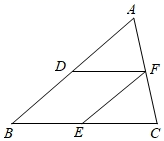 14. 在矩形ABCD中,对角线AC , BD交于点O , DE平分∠ADC , 交BC于点E , ∠BDE=15°,则∠COD= .
14. 在矩形ABCD中,对角线AC , BD交于点O , DE平分∠ADC , 交BC于点E , ∠BDE=15°,则∠COD= . 15. 如图所示,已知矩形 中, , 现将边 绕它的一个端点旋转,当另一端点恰好落在边 所在直线的点E处时,线段 的长度为
15. 如图所示,已知矩形 中, , 现将边 绕它的一个端点旋转,当另一端点恰好落在边 所在直线的点E处时,线段 的长度为
三、解答题
-
16. 如图,已知菱形ABCD,延长AD到点F,使 ,延长CD到点E,使DE=CD,顺次连接点A,C,F,E,A.求证:四边形ACFE是矩形.
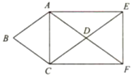 17. 如图,在平行四边形ABCD中,点P是AB边上一点(不与A,B重合),过点P作PQ⊥CP,交AD边于点Q,且∠QPA=∠PCB.
17. 如图,在平行四边形ABCD中,点P是AB边上一点(不与A,B重合),过点P作PQ⊥CP,交AD边于点Q,且∠QPA=∠PCB.求证:四边形ABCD是矩形.

四、综合题
-
18. 已知:如图,在平行四边形 中,G、H分别是 、 的中点,E、O、F分别是对角线 上的四等分点,顺次连接G、E、H、F.
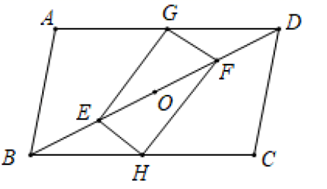 (1)、求证:四边形 是平行四边形;(2)、当平行四边形 满足条件时,四边形 是菱形;(3)、若 ,探究四边形 的形状,并说明理由.19. 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点E是斜边AB上的一个动点,连接CE,过点B,C分别作BD∥CE,CD∥BE,BD与CD相交于点D.
(1)、求证:四边形 是平行四边形;(2)、当平行四边形 满足条件时,四边形 是菱形;(3)、若 ,探究四边形 的形状,并说明理由.19. 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点E是斜边AB上的一个动点,连接CE,过点B,C分别作BD∥CE,CD∥BE,BD与CD相交于点D.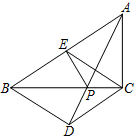 (1)、当CE⊥AB时,求证:四边形BECD是矩形;(2)、填空:
(1)、当CE⊥AB时,求证:四边形BECD是矩形;(2)、填空:①当BE的长为时,四边形BECD是菱形;
②在①的结论下,若点P是BC上一动点,连接AP,EP,则AP+EP的最小值为.