吉林省白城市通榆九中、育才学校2023-2024学年九年级上学期月考数学试卷(9月份)
试卷更新日期:2023-10-18 类型:月考试卷
一、选择题(本大题共6小题,共12.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 方程的一般式为时,的值为( )A、 B、 C、 D、2. 用配方法解一元二次方程时,配方正确的是( )A、 B、 C、 D、3. 一元二次方程的根是( )A、 B、 , C、 , D、4. 在某次聚会上,每两人都握了一次手,所有人共握手次,设有人参加这次聚会,则列出方程正确的是( )A、 B、 C、 D、5. 抛物线的图象如图所示,则与的大小关系是( )
 A、 B、 C、 D、不确定6. 如图,在长为 , 宽为的矩形空地上修筑四条宽度相等的小路,若余下的部分全部种上花卉,且花圃的面积是 , 则小路的宽是( )
A、 B、 C、 D、不确定6. 如图,在长为 , 宽为的矩形空地上修筑四条宽度相等的小路,若余下的部分全部种上花卉,且花圃的面积是 , 则小路的宽是( )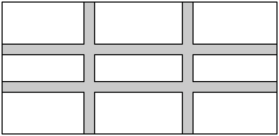 A、 B、 C、或 D、
A、 B、 C、或 D、二、填空题(本大题共8小题,共24.0分)
-
7. 已知是关于的一元二次方程,则的值为 .8. 将抛物线向上平移个单位长度,所得抛物线的解析式为 .9. 一元二次方程的根的判别式的值为 .10. 二次函数的顶点坐标是 .11. 抛物线的部分图象如图所示,则 .
 12. 某村年的人均收入为万元,年的人均收入为万元,则人均收入的年平均增长率为 .13. 坐标平面上有两个二次函数的图象,其顶点 , 均在轴上,且有一条水平线与两图象相交于 , , , 四点,各点位置如图所示,若 , , , 则的长度为 .
12. 某村年的人均收入为万元,年的人均收入为万元,则人均收入的年平均增长率为 .13. 坐标平面上有两个二次函数的图象,其顶点 , 均在轴上,且有一条水平线与两图象相交于 , , , 四点,各点位置如图所示,若 , , , 则的长度为 . 14. 已知二次函数 , 若点在该函数的图象上,且 , 则的值为.
14. 已知二次函数 , 若点在该函数的图象上,且 , 则的值为.三、解答题(本大题共12小题,共84.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 请你用直接开平方法解方程: .16. 请你用公式法解方程: .17. 已知抛物线过点 .(1)、求此抛物线的解析式.(2)、当函数值随的增大而增大时,直接写出的取值范围.18. 已知关于x的一元二次方程 有两个相等的实数根,求m的值.19. 某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,每个支干长出多少小分支?
20. 已知二次函数 , 其图象过点 .(1)、求此二次函数的解析式,并写出顶点的坐标.(2)、设此二次函数与轴交于 , 两点,直接写出的面积.21. 设二次函数是实数已知函数值和自变量的部分对应取值如表所示: (1)、求此二次函数的解析式.(2)、 ▲ , ▲ , 并在图中画出二次函数的大致图象.22. 已知关于的一元二次方程中, .(1)、解: , ,
(1)、求此二次函数的解析式.(2)、 ▲ , ▲ , 并在图中画出二次函数的大致图象.22. 已知关于的一元二次方程中, .(1)、解: , ,,
,此时 .
(2)、若关于的一元二次方程有两个相等的实数根,求方程的根.23. 如图,钢球从斜面顶端由静止开始沿斜面滚下,速度每秒增加 . (1)、写出滚动的距离单位:关于滚动的时间单位:的函数关系式提示:本题中,距离平均速度时间 , , 其中是开始时的速度(2)、如果斜面的长度是 , 钢球从斜面顶端滚到底端用多长时间?24. 阅读材料:
(1)、写出滚动的距离单位:关于滚动的时间单位:的函数关系式提示:本题中,距离平均速度时间 , , 其中是开始时的速度(2)、如果斜面的长度是 , 钢球从斜面顶端滚到底端用多长时间?24. 阅读材料:材料:若关于的一元二次方程的两个根为 , , 则 , ;
材料:已知一元二次方程的两个实数根分别为 , , 求的值.
解:一元二次方程的两个实数根分别为 , ,
, ,
则
根据上述材料,结合你所学的知识,完成下列问题:
(1)、材料理解:一元二次方程的两个根为 , , 则 , ;(2)、类比应用:已知一元二次方程的两根分别为、 , 求的值;(3)、思维拓展:已知实数、满足 , , 且 , 求的值.25. 某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。(1)、若商场想平均每天盈利1200元,每件衬衫应降价多少元?(2)、商场有可能每天平均盈利1300元吗?若有可能,应降价多少元?26. 如图,抛物线经过、两点,并交轴于另一点 , 点是抛物线的顶点,直线与轴交于点 . (1)、求此抛物线的解析式及顶点的坐标.(2)、点是对称轴上的一点.
(1)、求此抛物线的解析式及顶点的坐标.(2)、点是对称轴上的一点.当四边形为平行四边形时,求点的坐标.
点的坐标为 ▲ .
若点是抛物线上一动点,当以 , , , 为顶点的四边形是平行四边形时,直接写出所有满足条件的点的坐标.