吉林省松原市前郭一中、三中、蒙中2023-2024学年九年级上学期月考数学试卷(9月份)
试卷更新日期:2023-10-18 类型:月考试卷
一、选择题(本大题共6小题,共12.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 一元二次方程的一次项系数是( )A、5 B、 C、2 D、02. 一元二次方程根的判别式的值是( )A、33 B、23 C、17 D、3. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 用配方法解方程 , 配方后的方程是( )A、 B、 C、 D、5. 如图所示,直线为二次函数的图象的对称轴,则下列说法正确的是( )
 A、恒大于 B、 , 同号 C、异号 D、以上说法都不对6. “抖音直播带货”已经成为一种热门的销售方式,某抖音主播代销某一品牌的电子产品(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负责处理).销售中发现每件售价99元时,日销售量为200件,当每件电子产品每下降5元时,日销售量会增加10件.已知每售出1件电子产品,该主播需支付厂家和其他费用共50元,设每件电子产品售价为x(元),主播每天的利润为w(元),则w与x之间的函数解析式为( )A、 B、 C、 D、
A、恒大于 B、 , 同号 C、异号 D、以上说法都不对6. “抖音直播带货”已经成为一种热门的销售方式,某抖音主播代销某一品牌的电子产品(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负责处理).销售中发现每件售价99元时,日销售量为200件,当每件电子产品每下降5元时,日销售量会增加10件.已知每售出1件电子产品,该主播需支付厂家和其他费用共50元,设每件电子产品售价为x(元),主播每天的利润为w(元),则w与x之间的函数解析式为( )A、 B、 C、 D、二、填空题(本大题共8小题,共24.0分)
-
7. 小华在解一元二次方程时,只得出一个根是 , 则被他漏掉的一个根是 .8. 二次函数的图象如图所示,则的取值范围是 .
 9. 将抛物线向上平移3个单位长度,所得抛物线解析式为.10. 二次函数的最大值是 .11. 已知点 , 在抛物线上,且 , 则 . (填“<”或“>”或“=”)12. 如图,二次函数的图象与轴相交于和两点,当函数值时,自变量的取值范围是 .
9. 将抛物线向上平移3个单位长度,所得抛物线解析式为.10. 二次函数的最大值是 .11. 已知点 , 在抛物线上,且 , 则 . (填“<”或“>”或“=”)12. 如图,二次函数的图象与轴相交于和两点,当函数值时,自变量的取值范围是 .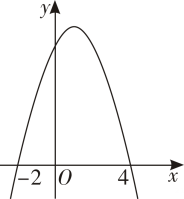 13. 如图,抛物线与轴相交于点、点 , 与轴相交于点 , 点在抛物线上,当轴时, .
13. 如图,抛物线与轴相交于点、点 , 与轴相交于点 , 点在抛物线上,当轴时, . 14. 如图,有一张长方形桌子的桌面长 , 宽 . 有一块长方形台布的面积是桌面面积的2倍,并且铺在桌面上时,各边垂下的长度相等.若设台布垂下的长度为 , 则可列出x满足的方程为 . (不必化简)
14. 如图,有一张长方形桌子的桌面长 , 宽 . 有一块长方形台布的面积是桌面面积的2倍,并且铺在桌面上时,各边垂下的长度相等.若设台布垂下的长度为 , 则可列出x满足的方程为 . (不必化简)

三、解答题(本大题共12小题,共84.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 解方程:16. 解方程: .17. 解方程:18. 已知抛物线经过点 .(1)、求的值;(2)、若点、都在该抛物线上,试比较与的大小.19. 已知关于的一元二次方程有两个不相等的实数根.(1)、求的取值范围;(2)、当时,用配方法解方程.20. 如图,已知抛物线的部分图象, , .
 (1)、求抛物线的解析式;(2)、若抛物线与轴的另一个交点是点,求的面积.21. 今年以来,长沙文旅各项数据增长强劲,长沙也是国内热门旅游目的地之一月日,五一商圈累计客流量将近万人次,其中外地游客占比左右长沙新消费品牌因人流量大也业绩喜人,文和友天接待客人约万人次.(1)、请你根据以上信息,判断以下三种说法是否正确对的打“”,错的打“”
(1)、求抛物线的解析式;(2)、若抛物线与轴的另一个交点是点,求的面积.21. 今年以来,长沙文旅各项数据增长强劲,长沙也是国内热门旅游目的地之一月日,五一商圈累计客流量将近万人次,其中外地游客占比左右长沙新消费品牌因人流量大也业绩喜人,文和友天接待客人约万人次.(1)、请你根据以上信息,判断以下三种说法是否正确对的打“”,错的打“”月日当天,长沙五一商圈本地游客占比左右 ;
今年长沙文和友五一期间平均每天接待客人约万人次 ;
(2)、另据一报道:长沙年五一假期,共接待游客约万大次,在年五一假期,共接待游客约万人次若年至年的年平均增长率保持相同,求出长沙年至年五一假期接待游客人次的年平均增长率.22. 已知二次函数 . (1)、用配方法将化成的形式;并写出对称轴和顶点坐标.(2)、在平面直角坐标系中,画出这个二次函数的草图;(3)、当时,直接写出y的取值范围.23. 年月日,商业首航完成中国民航商业运营国产大飞机正式起步12时分航班抵达北京首都机场,穿过隆重的“水门礼”寓意“接风洗尘”,是国际民航中高级别的礼仪如图 , 在一次“水门礼”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水柱近似看作形状相同的抛物线的一部分如图 , 当两辆消防车喷水口 , 的水平距离为米时,两条水柱在抛物线的顶点处相遇此时相遇点距地面米,喷水口 , 距地面均为米若两辆消防车同时后退米,两条水柱的形状及喷水口 , 到地面的距离均保持不变,求此时两条水柱相遇点距地面多少米.
(1)、用配方法将化成的形式;并写出对称轴和顶点坐标.(2)、在平面直角坐标系中,画出这个二次函数的草图;(3)、当时,直接写出y的取值范围.23. 年月日,商业首航完成中国民航商业运营国产大飞机正式起步12时分航班抵达北京首都机场,穿过隆重的“水门礼”寓意“接风洗尘”,是国际民航中高级别的礼仪如图 , 在一次“水门礼”的预演中,两辆消防车面向飞机喷射水柱,喷射的两条水柱近似看作形状相同的抛物线的一部分如图 , 当两辆消防车喷水口 , 的水平距离为米时,两条水柱在抛物线的顶点处相遇此时相遇点距地面米,喷水口 , 距地面均为米若两辆消防车同时后退米,两条水柱的形状及喷水口 , 到地面的距离均保持不变,求此时两条水柱相遇点距地面多少米. 24. 【观察思考】
24. 【观察思考】
【规律发现】
请用含的式子填空:
(1)、第个图案中“”的个数为 ;(2)、第个图案中“”的个数可表示为 , 第个图案中“”的个数可表示为 , 第个图案中“”的个数可表示为 , 第个图案中“”的个数可表示为 , , 第个图案中“”的个数可表示为 .(3)、【规律应用】
结合图案中“”的排列方式及上述规律,求正整数 , 使得连续的正整数之和等于第个图案中“”的个数的倍.