湖南省长沙市重点学校2023-2024学年八年级上学期入学数学试卷

试卷更新日期：2023-10-18 类型：开学考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 下列四个数中，是无理数的是（）

A、 $\sqrt{4}$ B、 $\frac{1}{2}$ C、 $\sqrt[3]{- 8}$ D、 $π$

查看试题解析
2. 下列各式是二元一次方程的是（）

A、 $2 x = 3 y + 1$ B、 $2 x - \frac{1}{3} x = - 1$ C、 $x + \frac{3}{y} = 0$ D、 $3 x y - 2 = y$

查看试题解析
3. 如图是小明探索直线平行的条件时所用的学具，木条 $a$ ， $b$ ， $c$ 在同一平面内，经测量，要使木条 $a / / b$ ， $∠ 2 = 110 °$ ，要使木条 $a$ 与 $b$ 平行，则 $∠ 1$ 的度数应为（）

A、 $20 °$ B、 $70 °$ C、 $110 °$ D、 $160 °$

查看试题解析
4. 下列调查中适合全面调查的是（）

A、对一批浏阳烟花的质量的调查 B、对湘江流域中的生物多样性情况的调查 C、对全国中学生的睡眠情况的调查 D、对宇宙空间站的零部件的检查

查看试题解析
5. 若 $m < 0$ ，则点 $P (- 3 ， m)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 如图， $A C$ 与 $B D$ 相交于点 $O$ ， $A B = D C$ ，要使 $△ A B O$ ≌ $△ D C O$ ，则需添加的一个条件可以是（）

A、 $O B = O C$ B、 $∠ A = ∠ D$ C、 $O A = O D$ D、 $∠ A O B = ∠ D O C$

查看试题解析
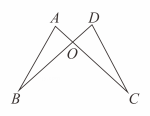7. 不等式 $9 - x > x + \frac{2}{3}$ 的正整数解的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 某校劳动课学习制作娃娃和沙包，已知每米布可做娃娃25个或沙包40个．现有36米布料，完成后打算将1个娃娃和2个沙包配成一套礼物．布料没有剩余，礼物也恰好成套．设做娃娃用了x米布，做沙包用了y米布，则（）

A、 $\{\begin{cases} x + y = 36 \\ y = 2 x \end{cases}$ B、 $\{\begin{cases} x + y = 36 \\ 25 x = 2 \times 40 y \end{cases}$ C、 $\{\begin{cases} x + y = 36 \\ 25 x = \frac{40 y}{2} \end{cases}$ D、 $\{\begin{cases} x + y = 36 \\ \frac{2 x}{25} = \frac{y}{40} \end{cases}$

查看试题解析
9. 如果三角形的两边长分别为 $2$ 和 $5$ ，那么这个三角形的周长可能是（）

A、 $10$ B、 $12$ C、 $14$ D、 $16$

查看试题解析
10. 如图在△ABC中，BO，CO分别平分∠ABC，∠ACB，交于O，CE为外角∠ACD的平分线，BO的延长线交CE于点E，记∠BAC=∠1，∠BEC=∠2，则以下结论①∠1=2∠2，②∠BOC=3∠2，③∠BOC=90°+∠1，④∠BOC=90°+∠2正确的是（）

A、①②③ B、①③④ C、①④ D、①②④

查看试题解析

二、填空题（本大题共6小题，共18.0分）

11. 若 $| b - 1 | + \sqrt{a + 2} = 0$ ，则 $(a + b)^{2023} =$ ．

查看试题解析
12. 若点 $P (m - 2 ， 5)$ 在 $y$ 轴上，则点 $P$ 的坐标为．

查看试题解析
13. 若方程组 ${\begin{array}{l} 5 x - 4 y = m \\ 5 y - 4 x = 8 \end{array}$ 的解满足 $x + y = 0$ ，则 $m$ 的值是．

查看试题解析
14. 若一个 $n$ 边形的每个内角都为 $120 °$ ，那么边数 $n$ 为．

查看试题解析
15. $4$ 月 $23$ 日为世界读书日，为了解八年级 $1000$ 学生的阅读时间，从中抽取 $300$ 名学生进行调查，则该调查中的样本容量是．

查看试题解析
16. 如图，在 $△ A B C$ 中， $B H ⊥ A C$ 交 $A C$ 于点 $H$ ， $C D$ 平分 $∠ A C B$ 交 $B H$ 于点 $D$ ， $△ D C H$ 的面积为 $4$ ， $△ B C D$ 的面积为 $8$ ， $C H = 3$ ，则 $B C$ 的长为．

查看试题解析

三、解答题（本大题共9小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）

17.

(1)、计算： $(\sqrt{3})^{2} + \sqrt[3]{- 8} + | \sqrt{3} - 2 |$ ；

(2)、解不等式组： ${\begin{array}{l} x - 3 (x - 1) \geq 1 \\ 1 + 3 x > x - 1 \end{array}$ ．

查看试题解析
18. 已知代数式 $a x^{2} + b x + c$ ，当 $x = 1$ 和 $x = - 3$ 时，它的值都为 $5$ ，当 $x = - 1$ 时，它的值为 $1$ ，

(1)、求 $a$ ， $b$ ， $c$ 的值；

(2)、当 $x = - 2$ 时，求代数式 $a x^{2} + b x + c$ 的值．

查看试题解析
19. 如图，点 $B$ 、 $E$ 、 $C$ 、 $F$ 在同一条直线上， $A C$ 与 $D E$ 相交于点 $O$ ， $A C / / D F$ ， $A B / / D E$ ， $B E = C F$ ．

(1)、求证： $A C = D F$ ；

(2)、若 $∠ E O C = 80 °$ ， $∠ F = 36 °$ ，求 $∠ B$ 的度数．

查看试题解析
20. 如图，在平面直角坐标系 $x O y$ 中，三角形 $A B C$ 三个顶点的坐标分别是 $A (4 ， 2)$ ， $B (1 ， 0)$ ， $C (5 ， - 3)$ ，三角形 $A B C$ 中任意一点 $P (x_{0} ， y_{0})$ ，经平移后对应点为 $P' (x_{0} - 6 ， y_{0} + 2)$ ，将三角形 $A B C$ 作同样的平移得到三角形 $A' B' C'$ ，点 $A$ ， $B$ ， $C$ 的对应点分别为 $A'$ ， $B'$ ， $C'$ ．

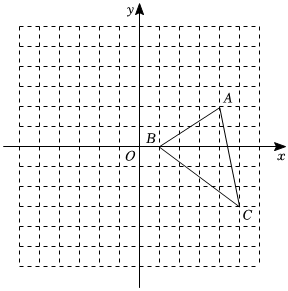(1)、 $A'$ 点的坐标为，点 $B'$ 的坐标为，点 $C'$ 的坐标为；

(2)、画出平移后的三角形 $A B' C'$ ；

(3)、计算求解 $△ A B C$ 的面积．

查看试题解析

21. 某校组织了一次“疫情防控知识”专题网上学习，并进行了一次全校

2500

名学生都参加的网上测试．阅卷后，教务处随机抽取

100

份答卷进行分析统计，绘制了频数分布表和频数分布直方图

(

不完整

)

，请结合图表信息回答下列问题：

分数段 $($ 分 $)$	频数 $($ 人 $)$
$51 \leq x < 61$	$10$
$61 \leq x < 71$	$18$
$71 \leq x < 81$	$a$
$81 \leq x < 91$	$35$
$91 \leq x < 101$	$12$
合计	$100$

(1)、

a =

，频数分布直方图的组距是；

(2)、补全频数分布直方图；

(3)、全校学生参加网上测试，成绩

x

在

81 \leq x < 101

范围内的学生约有多少人？

查看试题解析

22. 为更好地推进生活垃圾分类工作，改善城市生态环境，某小区准备购买A，B两种型号的垃圾箱，通过市场调研得知：购买3个A型垃圾箱和2个B型垃圾箱共需540元，购买2个A型垃圾箱比购买3个B型垃圾箱少用160元．

(1)、每个A型垃圾箱和B型垃圾箱分别是多少元？

(2)、若该小区物业计划用低于2150元的资金购买A，B两种型号的垃圾箱共20个，且至少购买6个B型垃圾箱，请问有几种购买方案？

查看试题解析
23. 如图， $A C ⊥ B C$ ， $A D ⊥ B D$ ， $A D = B C$ ， $C E ⊥ A B$ ， $D F ⊥ A B$ ，垂足分别是 $E$ ， $F$ ，
求证：
$① △ A B C$ ≌ $△ B A D$ ；
$② C E = D F$ ．

查看试题解析
24. 若一个不等式 $($ 组 $) A$ 有解且解集为 $a < x < b (a < b)$ ，则称 $\frac{a + b}{2}$ 为 $A$ 的解集中点值，若 $A$ 的解集中点值是不等式 $($ 组 $) B$ 的解 $($ 即中点值满足不等式组 $)$ ，则称不等式 $($ 组 $) B$ 对于不等式 $($ 组 $) A$ 中点包含．

(1)、已知关于 $x$ 的不等式组 $A$ ： ${\begin{array}{l} 2 x - 3 > 5 \\ 6 - x > 0 \end{array}$ ，以及不等式 $B$ ： $- 1 < x \leq 5$ ，请判断不等式 $B$ 对于不等式组 $A$ 是否中点包含，并写出判断过程；

(2)、已知关于 $x$ 的不等式组 $C$ ： ${\begin{array}{l} 2 x + 7 > 2 m + 1 \\ 3 x - 16 < 9 m - 1 \end{array}$ 和不等式组 $D$ ： ${\begin{array}{l} x > m - 4 \\ 3 x - 13 < 5 m \end{array}$ ，若 $D$ 对于不等式组 $C$ 中点包含，求 $m$ 的取值范围．

(3)、关于 $x$ 的不等式组 $E$ ： ${\begin{array}{l} x > 2 n \\ x < 2 m \end{array} (n < m)$ 和不等式组 $F$ ： ${\begin{array}{l} x - n < 5 \\ 2 x - m > 3 n \end{array}$ ，若不等式组 $F$ 对于不等式组 $E$ 中点包含，且所有符合要求的整数 $m$ 之和为 $9$ ，求 $n$ 的取值范围．

查看试题解析
25. 已知，在 $△ A B C$ 中， $A B = A C$ ， $D$ ， $A$ ， $E$ 三点都在直线 $m$ 上，且 $D E = 9 c m$ ， $∠ B D A = ∠ A E C = ∠ B A C$

(1)、如图 $①$ ，若 $A B ⊥ A C$ ，则 $B D$ 与 $A E$ 的数量关系为， $C E$ 与 $A D$ 的数量关系为；

(2)、如图 $②$ ，判断并说明线段 $B D$ ， $C E$ 与 $D E$ 的数量关系；

(3)、如图 $③$ ，若只保持 $∠ B D A = ∠ A E C$ ， $B D = E F = 7 c m$ ，点 $A$ 在线段 $D E$ 上以 $2 c m / s$ 的速度由点 $D$ 向点 $E$ 运动，同时，点 $C$ 在线段 $E F$ 上以 $x c m / s$ 的速度由点 $E$ 向点 $F$ 运动，它们运动的时间为 $t (s) .$ 是否存在 $x$ ，使得 $△ A B D$ 与 $△ E A C$ 全等？若存在，求出相应的 $t$ 的值；若不存在，请说明理由．

查看试题解析