山东省聊城市重点中学2023-2024学年九年级上学期月考数学试卷(9月)
试卷更新日期:2023-10-18 类型:月考试卷
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列各组图形中,一定是相似图形的是( )A、两个等腰梯形 B、两个矩形 C、两个直角三角形 D、两个等边三角形2. 如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是( )
 A、2 B、3 C、4 D、53. 如图,给出下列条件:;;; , 其中不能判定∽的条件为( )
A、2 B、3 C、4 D、53. 如图,给出下列条件:;;; , 其中不能判定∽的条件为( ) A、 B、 C、 D、4. 如图,矩形与矩形是位似图形,点是位似中心.若点的坐标为 , 点的横坐标为 , 则点的坐标为( )
A、 B、 C、 D、4. 如图,矩形与矩形是位似图形,点是位似中心.若点的坐标为 , 点的横坐标为 , 则点的坐标为( ) A、 B、 C、 D、5. 已知<cosA<sin80°,则锐角A的取值范围是( )A、60°<A<80° B、30°<A<80° C、10°<A<60° D、10°<A<30°6. 在中,若角 , 满足 , 则的大小是( )A、 B、 C、 D、7. 如图,在网格正方形中,每个小正方形的边长为1,顶点为格点,若的顶点均是格点,则的值是( )
A、 B、 C、 D、5. 已知<cosA<sin80°,则锐角A的取值范围是( )A、60°<A<80° B、30°<A<80° C、10°<A<60° D、10°<A<30°6. 在中,若角 , 满足 , 则的大小是( )A、 B、 C、 D、7. 如图,在网格正方形中,每个小正方形的边长为1,顶点为格点,若的顶点均是格点,则的值是( ) A、 B、 C、 D、8. 如图,在中, , , , 则的面积是( )
A、 B、 C、 D、8. 如图,在中, , , , 则的面积是( ) A、 B、 C、 D、9. 如图,在高为 , 坡角为的楼梯上铺地毯,地毯的长度至少应为( )
A、 B、 C、 D、9. 如图,在高为 , 坡角为的楼梯上铺地毯,地毯的长度至少应为( ) A、 B、 C、 D、10. 如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为 米,则斜坡AB的长度为( )
A、 B、 C、 D、10. 如图大坝的横断面,斜坡AB的坡比i=1:2,背水坡CD的坡比i=1:1,若坡面CD的长度为 米,则斜坡AB的长度为( ) A、 B、 C、 D、2411. 如图,在中, , , , 若内接正方形的边长是 , 则、、的数量关系为( )
A、 B、 C、 D、2411. 如图,在中, , , , 若内接正方形的边长是 , 则、、的数量关系为( ) A、 B、 C、 D、12. 在平面直角坐标系中,正方形的位置如图所示,点的坐标为 , 点的坐标为 , 延长交轴于点 , 作正方形;延长交轴于点 , 作正方形;;按这样的规律进行下去,正方形的面积为( )
A、 B、 C、 D、12. 在平面直角坐标系中,正方形的位置如图所示,点的坐标为 , 点的坐标为 , 延长交轴于点 , 作正方形;延长交轴于点 , 作正方形;;按这样的规律进行下去,正方形的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共8小题,共24.0分)
-
13. 如图,把一张矩形纸片平均分成个矩形,若每个小矩形都与原矩形相似,则原矩形纸片的宽与长之比为 .
 14. 若△ADE∽△ACB,且= , DE=10,则BC= .
14. 若△ADE∽△ACB,且= , DE=10,则BC= .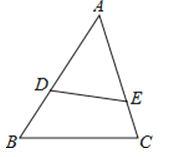 15. 一个多边形的边长分别为 , , , , 另一个与它相似的多边形的最长边长为 , 则该多边形的最短边长为 .16. 如图,在▱中,在上,、交于 , 若:: , 则: .
15. 一个多边形的边长分别为 , , , , 另一个与它相似的多边形的最长边长为 , 则该多边形的最短边长为 .16. 如图,在▱中,在上,、交于 , 若:: , 则: . 17. 如图,由边长为的小正方形组成的虚线网格中,点、、、为格点即小正方形的顶点 , 、相交于点 , 则的长为 .
17. 如图,由边长为的小正方形组成的虚线网格中,点、、、为格点即小正方形的顶点 , 、相交于点 , 则的长为 .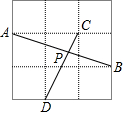 18. 已知为锐角,且 , 则等于度.19. 如图,在边长相同的小正方形网格中,点、、、都在这些小正方形的顶点上,与相交于点 , 则的值为 .
18. 已知为锐角,且 , 则等于度.19. 如图,在边长相同的小正方形网格中,点、、、都在这些小正方形的顶点上,与相交于点 , 则的值为 . 20. 如图,海上有一灯塔 , 位于小岛北偏东方向上,一艘轮船从小岛出发,由西向东航行到达处,这时测得灯塔在北偏东方向上,如果轮船不改变航向继续向东航行,当轮船到达灯塔的正南方,此时轮船与灯塔的距离是结果保留一位小数,约等于
20. 如图,海上有一灯塔 , 位于小岛北偏东方向上,一艘轮船从小岛出发,由西向东航行到达处,这时测得灯塔在北偏东方向上,如果轮船不改变航向继续向东航行,当轮船到达灯塔的正南方,此时轮船与灯塔的距离是结果保留一位小数,约等于
三、解答题(本大题共5小题,共60.0分。解答应写出文字说明,证明过程或演算步骤)
-
21. 如图,在网格图中小正方形的边长为 , 的三个顶点都在格点上.

⑴把沿着轴向右平移个单位得到 , 请画出;
⑵请以坐标系的原点点为位似中心在第一象限内画出的位似图形 , 使得与的位似比为:;
⑶请直接写出三个顶点的坐标.
22. 如图,是平行四边形的边上的一点,连结并延长交的延长线于点 . (1)、求证:∽;(2)、若 , , 的面积为 , 求平行四边形的面积.23. 已知 , 延长到 , 使取的中点 , 连接交于点 .
(1)、求证:∽;(2)、若 , , 的面积为 , 求平行四边形的面积.23. 已知 , 延长到 , 使取的中点 , 连接交于点 . (1)、求的值;(2)、若 , , 求的长.24. 如图,小明为了测量小河对岸大树的高度,他在点测得大树顶端的仰角是 , 沿斜坡走米到达斜坡上点 , 在此处测得树顶端点的仰角为 , 且斜坡的坡比为:参考数据: , , .
(1)、求的值;(2)、若 , , 求的长.24. 如图,小明为了测量小河对岸大树的高度,他在点测得大树顶端的仰角是 , 沿斜坡走米到达斜坡上点 , 在此处测得树顶端点的仰角为 , 且斜坡的坡比为:参考数据: , , . (1)、求小明从点走到点的过程中,他上升的高度;(2)、大树的高度约为多少米?25. 为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时40海里的速度向正东方航行,在 处测得灯塔 在北偏东60°方向上,继续航行1小时到达 处,此时测得灯塔 在北偏东30°方向上.
(1)、求小明从点走到点的过程中,他上升的高度;(2)、大树的高度约为多少米?25. 为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时40海里的速度向正东方航行,在 处测得灯塔 在北偏东60°方向上,继续航行1小时到达 处,此时测得灯塔 在北偏东30°方向上.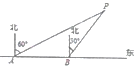 (1)、求 的度数;(2)、已知在灯塔 的周围20海里内有暗礁,问海监船继续向正东方向航行是否安全?
(1)、求 的度数;(2)、已知在灯塔 的周围20海里内有暗礁,问海监船继续向正东方向航行是否安全?