安徽省六安市2023-2024学年八年级上学期第一次月考数学试卷
试卷更新日期:2023-10-18 类型:月考试卷
一、单选题(每题4分,共40分)
-
1. 在平面直角坐标系中,点P(-3,8)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 在平面直角坐标系中,已知点4(-1,2), B(10),平移线段AB,使点A落在点A1(2,3)处,则点B的对应点B1的坐标为( )A、(-2,-1) B、(4,1) C、(4,0) D、(-2,1)3. 若正比例函数的图像经过点和点 , 当时, , 则的取值范围是( )A、 B、 C、 D、4. 如图所示,一次函数是常数,与正比例函数是常数,的图象相交于点 , 下列判断错误的是( )
 A、关于的方程的解是 B、关于的不等式的解集是 C、当时,函数的值比函数的值大 D、关于 , 的方程组 的解是5. 若一次函数的图象不经过第三象限,则的取值范围是( )A、 B、 C、 D、6. 某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间.出发时油箱中存油40升,到B地后发现油箱中还剩油4升,则从出发后到B地油箱中所剩油y(升)与时间t(小时)之间函数的大致图象是( )A、
A、关于的方程的解是 B、关于的不等式的解集是 C、当时,函数的值比函数的值大 D、关于 , 的方程组 的解是5. 若一次函数的图象不经过第三象限,则的取值范围是( )A、 B、 C、 D、6. 某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间.出发时油箱中存油40升,到B地后发现油箱中还剩油4升,则从出发后到B地油箱中所剩油y(升)与时间t(小时)之间函数的大致图象是( )A、 B、
B、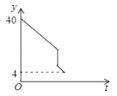 C、
C、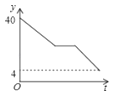 D、
D、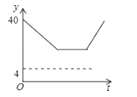 7. 已知 , 均为关于x的函数,当 时,函数值分别为 , ,若对于实数a,当 时,都有 ,则称 , 为亲函数,则以下函数 和 是亲函数的是( )A、 , B、 , C、 , D、 ,8. 象棋在中国有着三千多年的历史,如图是一方的棋盘,如果“帅”的坐标是(1,1),“卒”的坐标是(3,2),那么“马”的坐标是( )
7. 已知 , 均为关于x的函数,当 时,函数值分别为 , ,若对于实数a,当 时,都有 ,则称 , 为亲函数,则以下函数 和 是亲函数的是( )A、 , B、 , C、 , D、 ,8. 象棋在中国有着三千多年的历史,如图是一方的棋盘,如果“帅”的坐标是(1,1),“卒”的坐标是(3,2),那么“马”的坐标是( )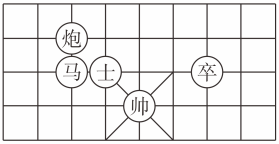 A、 B、 C、 D、9. 一次函数与正比例函数为常数,且),它们在同一坐标系中的大致图象是( )A、
A、 B、 C、 D、9. 一次函数与正比例函数为常数,且),它们在同一坐标系中的大致图象是( )A、 B、
B、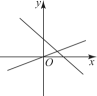 C、
C、 D、
D、 10.
10.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,1),B(2,1), C(1,3). 若直线y=3x+b与△ABC的边至少有两个交点,则b的取值范围是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题5分,共20分)
-
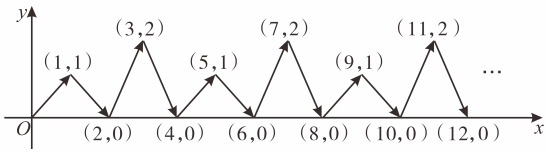
11. 函数y= 中自变量x的取值范围是 .12. 已知直线y=kx+b与直线y=-3x平行,且经过点(2,4),则b的值是 .13. 若一次函数y=2x+b与坐标轴围成的三角形面积为9,则这个一次函数的解析式为 .14. 如图,点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……,按这样的运动规律,经过第2025次运动后动点P的坐标是 .
三、解答题(90分)
-
15. 已知A、B、C的坐标分别为试判断A、B、C三点是否在同一直线上,并说明理由.16. 如图,在平面直角坐标系中.已知把三角形ABC先向左平移2个单位长度,再向下平移4个単位长度得到三角形DEF.
 (1)、写出D,E,F三点的坐标;(2)、画出三角形DEF;(3)、求三角形DEF的面积.17. 已知:y-2与x−3成正比例,且x=4时y=8.(1)、求y与x之间的函数关系式;(2)、当y=-6时,求x的值.18. 已知:一次函数 .(1)、若一次函数的图象过原点,求实数m的值;(2)、当一次函数的图象经过第二、三、四象限时,求实数m的取值范围;(3)、当一次函数的图象不经过第三象限时,求实数m的取值范围.19. 某公交车每天的支出费用为600元,每天的乘车人数x(人)与每天利润(利润=票款收入-支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变):
(1)、写出D,E,F三点的坐标;(2)、画出三角形DEF;(3)、求三角形DEF的面积.17. 已知:y-2与x−3成正比例,且x=4时y=8.(1)、求y与x之间的函数关系式;(2)、当y=-6时,求x的值.18. 已知:一次函数 .(1)、若一次函数的图象过原点,求实数m的值;(2)、当一次函数的图象经过第二、三、四象限时,求实数m的取值范围;(3)、当一次函数的图象不经过第三象限时,求实数m的取值范围.19. 某公交车每天的支出费用为600元,每天的乘车人数x(人)与每天利润(利润=票款收入-支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变):x(人)
…
200
250
300
350
400
…
y(元)
…
-200
-100
0
100
200
…
(1)、观察表中数据可知,若要保证不亏本,该公交车每天乘客应达到多少人?(2)、请你估计一天乘客人数为500人时,利润是多少?(3)、写出y与x的关系表达式.20. 如图,已知直线与坐标轴交于两点,直线与坐标轴交于两点,两直线的交点为. (1)、求k,a,b的值;(2)、连接OM,试说明(s表示面积);(3)、x轴上存在点T,使得 , 求出此时点T的坐标.21. 某电信公司手机的A类收费标准如下:不管通话时间多长,每部手机每月必须缴月租费12元,另外,通话费按0.2元/min计;B类收费标准如下:没有月租费,但通话费按0.6元/min计.按照此类收费标准完成下列各题:(1)、直接写出每月应缴费用y(元)与通话时长x(分)之间的关系式:
(1)、求k,a,b的值;(2)、连接OM,试说明(s表示面积);(3)、x轴上存在点T,使得 , 求出此时点T的坐标.21. 某电信公司手机的A类收费标准如下:不管通话时间多长,每部手机每月必须缴月租费12元,另外,通话费按0.2元/min计;B类收费标准如下:没有月租费,但通话费按0.6元/min计.按照此类收费标准完成下列各题:(1)、直接写出每月应缴费用y(元)与通话时长x(分)之间的关系式:A类:;B类: .
(2)、若每月平均通话时长为300分钟,选择类收费方式较少.(3)、求每月通话多长时间时,按A,B两类收费标准缴费,所缴话费相等.22. 一列火车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的关系,根据图像进行以下探究: (1)、甲、乙两地的距离为多少km;(2)、请解释图中点B的实际意义;(3)、求慢车与快车的速度.23. 某校为达成省体育器材类装备,计划在京东惠购一次性购进篮球和足球共50个,某电商内部信息表给出其进价与售价间的关系如下表:
(1)、甲、乙两地的距离为多少km;(2)、请解释图中点B的实际意义;(3)、求慢车与快车的速度.23. 某校为达成省体育器材类装备,计划在京东惠购一次性购进篮球和足球共50个,某电商内部信息表给出其进价与售价间的关系如下表:篮球
足球
进价(元/个)
105
90
售价(元/个)
135
125
(1)、学校用4920元以进价购进这批篮球和足球,求购进篮球和足球各多少个;(2)、设该电商所获利润为y(单位:元),购进篮球的个数为x(单位:个),请写出y与x之间的函数表达式(不要求写出x的取值范围);(3)、因资金紧张,学校的进货成本只能在4745元的限额内,请为学校设计一种进货方案使得尽可能多地购买篮球和足球,同时要使电商利润最小;并求出利润的最小值.