河北省保定市涿州重点中学2023-2024学年八年级上学期第一次月考数学试卷
试卷更新日期:2023-10-18 类型:月考试卷
一、选择题(本大题共16小题,共32.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列图形具有稳定性的是( )A、
 B、
B、 C、
C、 D、
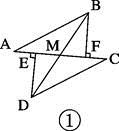
D、 2. 如图,在△ABC中有四条线段DE,BE,EF,FG,其中有一条线段是△ABC的中线,则该线段是( )
2. 如图,在△ABC中有四条线段DE,BE,EF,FG,其中有一条线段是△ABC的中线,则该线段是( ) A、线段DE B、线段BE C、线段EF D、线段FG3. 下列线段能组成三角形的是( )A、 , , B、 , , C、 , , D、 , ,4.
A、线段DE B、线段BE C、线段EF D、线段FG3. 下列线段能组成三角形的是( )A、 , , B、 , , C、 , , D、 , ,4.如图,在△ABC中,D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A等于( )
 A、60° B、70° C、80° D、90°5. 如图,≌ , 点点 , 点和点是对应点.如果厘米,厘米,厘米,那么的长是( )
A、60° B、70° C、80° D、90°5. 如图,≌ , 点点 , 点和点是对应点.如果厘米,厘米,厘米,那么的长是( ) A、 厘米 B、厘米 C、 厘米 D、无法确定6. 若一个正多边形的内角和为720°,则这个正多边形的每一个内角是( )A、60° B、90° C、108° D、120°7. 如图,五边形中, , 、、分别是、、的邻补角,则等于( )
A、 厘米 B、厘米 C、 厘米 D、无法确定6. 若一个正多边形的内角和为720°,则这个正多边形的每一个内角是( )A、60° B、90° C、108° D、120°7. 如图,五边形中, , 、、分别是、、的邻补角,则等于( ) A、 B、 C、 D、8. 下列各组图形中,是的高的图形是( )A、
A、 B、 C、 D、8. 下列各组图形中,是的高的图形是( )A、 B、
B、 C、
C、 D、
D、 9. 小明同学在用计算器计算某边形的内角和时,不小心多输入一个内角,得到和为 , 则等于( )A、 B、 C、 D、10. 边长都为整数的△ABC≌△DEF ,AB与DE是对应边,AB=2,BC=4,若△DEF的周长为偶数,则 DF的取值为( )A、3 B、4 C、5 D、3或4或511. 如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
9. 小明同学在用计算器计算某边形的内角和时,不小心多输入一个内角,得到和为 , 则等于( )A、 B、 C、 D、10. 边长都为整数的△ABC≌△DEF ,AB与DE是对应边,AB=2,BC=4,若△DEF的周长为偶数,则 DF的取值为( )A、3 B、4 C、5 D、3或4或511. 如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )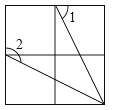 A、150° B、180° C、210° D、225°12. 如图,在中, , , 是上一点将沿折叠,使点落在边上的处,则等于( )
A、150° B、180° C、210° D、225°12. 如图,在中, , , 是上一点将沿折叠,使点落在边上的处,则等于( ) A、 B、 C、 D、13. 如图,在证明“内角和等于”时,延长至点 , 过点作 , 得到 , , 由于 , 可得到 , 这个证明方法体现的数学思想是( )
A、 B、 C、 D、13. 如图,在证明“内角和等于”时,延长至点 , 过点作 , 得到 , , 由于 , 可得到 , 这个证明方法体现的数学思想是( ) A、数形结合 B、特殊到一般 C、一般到特殊 D、转化14. 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,若∠BFC=116°,则∠A=( )
A、数形结合 B、特殊到一般 C、一般到特殊 D、转化14. 如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,若∠BFC=116°,则∠A=( )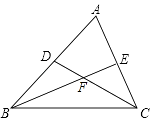 A、51° B、52° C、53° D、58°15. 两本书按如图所示方式叠放在一起,则图中相等的角是( )
A、51° B、52° C、53° D、58°15. 两本书按如图所示方式叠放在一起,则图中相等的角是( ) A、与 B、与 C、与 D、三个角都相等16. 如图,已知点和点 , 在坐标轴上确定点 , 使得为直角三角形,则满足这样条件的点共有( )
A、与 B、与 C、与 D、三个角都相等16. 如图,已知点和点 , 在坐标轴上确定点 , 使得为直角三角形,则满足这样条件的点共有( ) A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题(本大题共4小题,共8.0分)
-
17. 等腰三角形的两边长分别为4和9,则第三边长为18. 三角形三边长分别为3, , 则a的取值范围是 .19. 中, , , 则的度数是 .20. 如图,给正五边形的顶点依次编号为 , , , , 若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.
如:小宇在编号为的顶点上时,那么他应走个边长,即从为第一次“移位”,这时他到达编号为的顶点;然后从为第二次“移位”.
若小宇从编号为的顶点开始,第次“移位”后,则他所处顶点的编号是 .

三、解答题(本大题共6小题,共60.0分。解答应写出文字说明,证明过程或演算步骤)
-
21. 如图,为的中线,为三角形中线,
 (1)、在中作边上的高;(2)、若的面积为 , , 求的长.22. 如图,已知点B、D、E、C四点在一条直线上,且△ABE≌△ACD.
(1)、在中作边上的高;(2)、若的面积为 , , 求的长.22. 如图,已知点B、D、E、C四点在一条直线上,且△ABE≌△ACD.
求证
(1)、BD=CE;(2)、△ABD≌△ACE.23. 如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.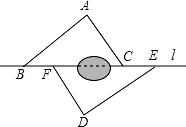 (1)、求证:△ABC≌△DEF;(2)、指出图中所有平行的线段,并说明理由.24. 如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中的变化情况,解答下列问题.
(1)、求证:△ABC≌△DEF;(2)、指出图中所有平行的线段,并说明理由.24. 如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形,如图,就是一组正多边形,观察每个正多边形中的变化情况,解答下列问题. (1)、将下面的表格补充完整:
(1)、将下面的表格补充完整:正多边形的边数
的度数
(2)、根据规律,是否存在一个正边形,使其中的?若存在,直接写出的值;若不存在,请说明理由.(3)、根据规律,是否存在一个正边形,使其中的?若存在,直接写出的值;若不存在,请说明理由.