河北省石家庄市裕华区2022-2023学年八年级下学期期末数学试卷
试卷更新日期:2023-10-18 类型:期末考试
一、选择题(本大题共12小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 为了了解年石家庄市九年级学生学业水平考试的数学成绩,从中随机抽取了名学生的数学成绩下列说法正确的是( )A、年石家庄市九年级学生是总体 B、每一名九年级学生是个体 C、名九年级学生是总体的一个样本 D、样本容量是2. 如图,在平面直角坐标系中,☆盖住的点的坐标可能是( )
 A、 B、 C、 D、3. 如图,将四边形纸片剪掉一角得五边形,则所得新图形的外角和与原图形的外角和之间的关系是( )
A、 B、 C、 D、3. 如图,将四边形纸片剪掉一角得五边形,则所得新图形的外角和与原图形的外角和之间的关系是( )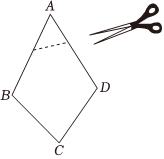 A、增加了 B、增加了 C、没有变化 D、不能判断4. 如图,在平面直角坐标系中,有一只蜗牛从点的位置沿着射线的方向爬行到另一象限的点 , 恰好 , 则点的坐标为( )
A、增加了 B、增加了 C、没有变化 D、不能判断4. 如图,在平面直角坐标系中,有一只蜗牛从点的位置沿着射线的方向爬行到另一象限的点 , 恰好 , 则点的坐标为( ) A、 B、 C、 D、5. 如图, , 两地被池塘隔开,小明在外选一点 , 连接 , , 分别取 , 的中点 , , 为了测量 , 两地间的距离,则可以选择测量以下线段中哪一条的长度( )
A、 B、 C、 D、5. 如图, , 两地被池塘隔开,小明在外选一点 , 连接 , , 分别取 , 的中点 , , 为了测量 , 两地间的距离,则可以选择测量以下线段中哪一条的长度( )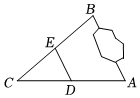 A、 B、 C、 D、6. 如图,在一次活动中,位于处的班准备前往相距的处于班会合,用方向和距离描述班相对于班的位置( )
A、 B、 C、 D、6. 如图,在一次活动中,位于处的班准备前往相距的处于班会合,用方向和距离描述班相对于班的位置( )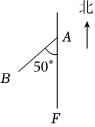 A、班在班南偏西处 B、班在班南偏西方向上处 C、班在班处 D、班在班北偏东方向上处7. 如图,与的形状相同,大小不同,是由的各顶点变化得到的,则各顶点变化情况( )
A、班在班南偏西处 B、班在班南偏西方向上处 C、班在班处 D、班在班北偏东方向上处7. 如图,与的形状相同,大小不同,是由的各顶点变化得到的,则各顶点变化情况( )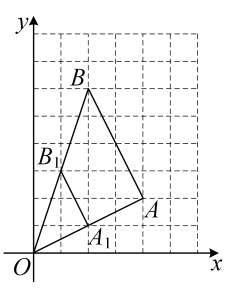 A、横坐标和纵坐标都加 B、横坐标和纵坐标都乘以 C、横坐标和纵坐标都除以 D、横坐标和纵坐标都减8. 对于函数 , 下列说法不正确的是( )A、该函数是正比例函数 B、该函数图象过点 C、该函数图象经过一、三象限 D、随着的增大而增大9. 依据所标数据,下列不一定是矩形的为( )A、
A、横坐标和纵坐标都加 B、横坐标和纵坐标都乘以 C、横坐标和纵坐标都除以 D、横坐标和纵坐标都减8. 对于函数 , 下列说法不正确的是( )A、该函数是正比例函数 B、该函数图象过点 C、该函数图象经过一、三象限 D、随着的增大而增大9. 依据所标数据,下列不一定是矩形的为( )A、 B、
B、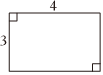 C、
C、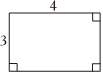 D、
D、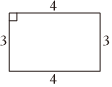 10. 如图,已知直线与相交于点 , 则关于的不等式的解集在数轴上表示正确的是( )
10. 如图,已知直线与相交于点 , 则关于的不等式的解集在数轴上表示正确的是( )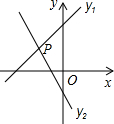 A、
A、 B、
B、 C、
C、 D、
D、 11. 将2×2的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上,若直线y=kx(k≠0)与正方形ABCD有公共点,则k不可能是( )
11. 将2×2的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上,若直线y=kx(k≠0)与正方形ABCD有公共点,则k不可能是( )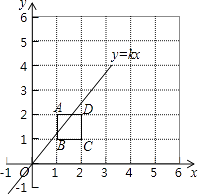 A、3 B、2 C、1 D、12. 对于题目,“在长为的线段上取一点 , 使 , 以为边向上作矩形 , 且 , 点从点出发,沿射线方向以每秒个单位长的速度运动,点从点出发,先以每秒个单位长的速度向点运动,到达点后,再以每秒个单位长的速度沿射线方向运动,已知、同时出发,运动时间为 , 若以、、 , 为顶点的四边形是平行四边形,求的值”,甲答: , 乙答,( )
A、3 B、2 C、1 D、12. 对于题目,“在长为的线段上取一点 , 使 , 以为边向上作矩形 , 且 , 点从点出发,沿射线方向以每秒个单位长的速度运动,点从点出发,先以每秒个单位长的速度向点运动,到达点后,再以每秒个单位长的速度沿射线方向运动,已知、同时出发,运动时间为 , 若以、、 , 为顶点的四边形是平行四边形,求的值”,甲答: , 乙答,( )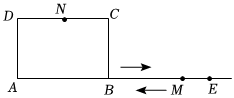 A、只有甲答的对 B、只有乙答的对 C、甲、乙答案合在一起才完整 D、甲、乙答案合在一起也不完整
A、只有甲答的对 B、只有乙答的对 C、甲、乙答案合在一起才完整 D、甲、乙答案合在一起也不完整二、填空题(本大题共6小题,共18.0分)
-
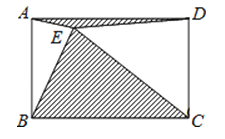
13. 函数y= 中自变量x的取值范围是 .14. 一次函数的图象向上平移 个单位后经过点 .15. 如图,点E是矩形ABCD内任一点,若AB=3,BC=4.则图中阴影部分的面积为
 16. 已知一次函数 的图象经过 , 两点,则 (填“ ”“ ”或“ ”).17. 某医药研究所研发了一种新药,经临床实验发现,成人按规定剂量服用,每毫升血液中含药量(微克)随时间(小时)而变化的情况如图所示.研究表明,当血液中含药量(微克)时,对治疗疾病有效,则有效时间是小时.
16. 已知一次函数 的图象经过 , 两点,则 (填“ ”“ ”或“ ”).17. 某医药研究所研发了一种新药,经临床实验发现,成人按规定剂量服用,每毫升血液中含药量(微克)随时间(小时)而变化的情况如图所示.研究表明,当血液中含药量(微克)时,对治疗疾病有效,则有效时间是小时.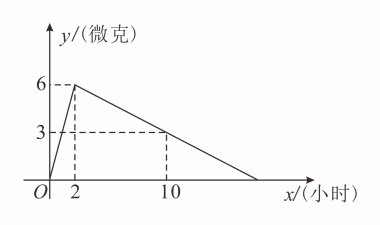 18. 如图,菱形的对角线 , 相交于点 , 点为边上一动点不与点 , 重合 , 于点 , 于点 , 若 , , 则的最小值为 .
18. 如图,菱形的对角线 , 相交于点 , 点为边上一动点不与点 , 重合 , 于点 , 于点 , 若 , , 则的最小值为 .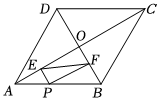
三、解答题(本大题共8小题,共58.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 如图所示,在平面直角坐标系中,的三个顶点坐标分别为 .
 (1)、在图中画出关于轴对称的图形;(2)、在图中,若与点关于一条直线成轴对称,则这条对称轴是 , 此时点关于这条直线的对称点的坐标为;(3)、求的面积.20. 购物支付方式日益增多,主要有:微信,支付宝,现金,其他数学兴趣小组对消费者的支付方式进行了抽样调查,得到如两幅不完整的统计图请你根据统计图提供的信息,解答下列问题:
(1)、在图中画出关于轴对称的图形;(2)、在图中,若与点关于一条直线成轴对称,则这条对称轴是 , 此时点关于这条直线的对称点的坐标为;(3)、求的面积.20. 购物支付方式日益增多,主要有:微信,支付宝,现金,其他数学兴趣小组对消费者的支付方式进行了抽样调查,得到如两幅不完整的统计图请你根据统计图提供的信息,解答下列问题: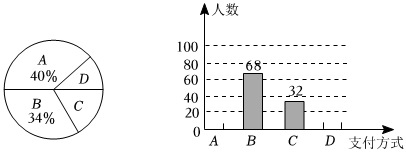 (1)、本次一共调查了多少名消费者?(2)、补全条形统计图;(3)、求扇形统计图中对应的圆心角度数.21. 如图,直线的图象与轴交于点 , 直线的图象与轴交于点 , 两者相交于点 .
(1)、本次一共调查了多少名消费者?(2)、补全条形统计图;(3)、求扇形统计图中对应的圆心角度数.21. 如图,直线的图象与轴交于点 , 直线的图象与轴交于点 , 两者相交于点 .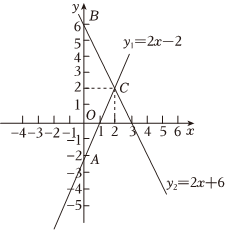 (1)、方程组的解是 ;(2)、当与同时成立时,的取值范围为 ;(3)、在直线的图象上存在异于点的另一点 , 使得与的面积相等,求出点的坐标.22. 如图 , ▱中, , 为锐角要在对角线上找点 , , 使四边形为平行四边形,现有图中的甲、乙、丙三种方案
(1)、方程组的解是 ;(2)、当与同时成立时,的取值范围为 ;(3)、在直线的图象上存在异于点的另一点 , 使得与的面积相等,求出点的坐标.22. 如图 , ▱中, , 为锐角要在对角线上找点 , , 使四边形为平行四边形,现有图中的甲、乙、丙三种方案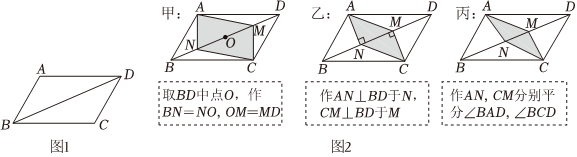 (1)、正确的方案有 种;(2)、针对上述三种作图方案,请从你认为正确的方案中选择一种给出证明过程.23. 枣庄某公交车每天的支出费用为元,每天的乘车人数人与每天利润利润票款收入支出费用元的变化关系,如下表所示每位乘客的乘车票价固定不变:
(1)、正确的方案有 种;(2)、针对上述三种作图方案,请从你认为正确的方案中选择一种给出证明过程.23. 枣庄某公交车每天的支出费用为元,每天的乘车人数人与每天利润利润票款收入支出费用元的变化关系,如下表所示每位乘客的乘车票价固定不变:人
元
根据表格中的数据,回答下列问题:
(1)、 是自变量;(2)、观察表中数据可知,当乘客量达到 人以上时,该公交车才不会亏损;(3)、请写出公交车每天利润元与每天乘车人数人的关系式: ;(4)、当一天乘客人数为多少人时,利润是元?24. 如图,在中, , 过点的直线 , 为上一点,过点作 , 交直线于点 , 垂足为 , 连接 , .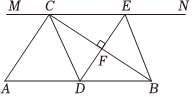 (1)、求证:;(2)、当点是的中点时,四边形是什么特殊四边形?请说明你的理由;(3)、请直接写出在的条件下,当 时,四边形是正方形.25. 某学校积极响应合肥市“争创全国文明典范城市”的号召,绿化校园,美化校园,计划购进 , 两种树苗,共45棵,已知种树苗每棵80元,种树苗每棵50元.设购买种树苗棵,购买两种树苗所需费用为元.(1)、求与的函数表达式;(2)、若购买种树苗的数量不少于种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.26. 如图,直角坐标系 中,过点 的直线 与直线 : 相交于点 ,直线 与x轴交于点B.
(1)、求证:;(2)、当点是的中点时,四边形是什么特殊四边形?请说明你的理由;(3)、请直接写出在的条件下,当 时,四边形是正方形.25. 某学校积极响应合肥市“争创全国文明典范城市”的号召,绿化校园,美化校园,计划购进 , 两种树苗,共45棵,已知种树苗每棵80元,种树苗每棵50元.设购买种树苗棵,购买两种树苗所需费用为元.(1)、求与的函数表达式;(2)、若购买种树苗的数量不少于种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.26. 如图,直角坐标系 中,过点 的直线 与直线 : 相交于点 ,直线 与x轴交于点B.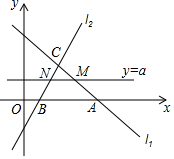 (1)、k的值为;(2)、求 的函数表达式和 的值;(3)、直线 与直线 和直线 分别交于点M,N,(M,N不同)
(1)、k的值为;(2)、求 的函数表达式和 的值;(3)、直线 与直线 和直线 分别交于点M,N,(M,N不同)①直接写出M,N都在y轴右侧时a的取值范围;
②在①的条件下,以 为边作正方形 ,边 恰好在x轴上,直接写出此时a的值.