河北省石家庄市辛集市2022-2023学年八年级下学期期末数学试卷
试卷更新日期:2023-10-18 类型:期末考试
一、选择题(本大题共16小题,共42.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 是一个正整数,则n的最小正整数是( )A、1 B、2 C、3 D、42. 下列计算正确的是( )A、 B、 C、 D、3. 下列说法不正确的是( )A、正方形面积公式中有两个变量: , B、圆的面积公式中的是常量 C、在一个关系式中,用字母表示的量可能不是变量 D、如果 , 那么 , 都是常量4. 五名同学捐款数分别是 , , , , 单位:元 , 捐元的同学后来又追加了元,追加后的个数据与之前的个数据相比,下列判断正确的是( )A、只有平均数相同 B、只有中位数相同 C、只有众数相同 D、中位数和众数都相同5. 在△ABC中,BC=a,AC=b,AB=c,根据下列条件不能判断△ABC是直角三角形的是( )A、∠B=50°,∠C=40° B、∠A=2∠B=3∠C C、a=4,b= , c=5 D、a:b:c=1::6. 在平行四边形的复习课上,小明绘制了如下知识框架图,箭头处添加条件错误的是( )
 A、①:对角线相等 B、②:对角互补 C、③:一组邻边相等 D、④:有一个角是直角7. 初中三年学习生涯,让懵懂青涩的少年逐渐成长为奋发向上的青年.比较九班名同学三年前后的年龄数据,在平均数、众数、中位数和方差四个统计量中,大小没有发生变化的统计量是( )A、平均数 B、众数 C、中位数 D、方差8. 容积为升的蓄水池装有一个进水管和一个出水管,单位时间内进、出水量都一定,单开进水管分钟可把空池注满,单开出水管分钟可把满池的水放尽.现水池内有水升,先打开进水管分钟后,再两管同时开放,直至把池中的水放完.这一过程中蓄水池中的蓄水量升随时间分变化的图象是( )A、
A、①:对角线相等 B、②:对角互补 C、③:一组邻边相等 D、④:有一个角是直角7. 初中三年学习生涯,让懵懂青涩的少年逐渐成长为奋发向上的青年.比较九班名同学三年前后的年龄数据,在平均数、众数、中位数和方差四个统计量中,大小没有发生变化的统计量是( )A、平均数 B、众数 C、中位数 D、方差8. 容积为升的蓄水池装有一个进水管和一个出水管,单位时间内进、出水量都一定,单开进水管分钟可把空池注满,单开出水管分钟可把满池的水放尽.现水池内有水升,先打开进水管分钟后,再两管同时开放,直至把池中的水放完.这一过程中蓄水池中的蓄水量升随时间分变化的图象是( )A、 B、
B、 C、
C、 D、
D、 9. 船航行的海岸附近有暗礁,为了使船不触上暗礁,可以在暗礁的两侧建立两座灯塔只要留心从船上到两个灯塔间的角度不超过一定的大小,就不用担心触礁如图所示的网格是正方形网格,点 , , , , , , 是网格线交点,当船航行到点的位置时,此时与两个灯塔 , 间的角度的大小一定无触礁危险那么,对于 , , , 四个位置,船处于____时,也一定无触礁危险( )
9. 船航行的海岸附近有暗礁,为了使船不触上暗礁,可以在暗礁的两侧建立两座灯塔只要留心从船上到两个灯塔间的角度不超过一定的大小,就不用担心触礁如图所示的网格是正方形网格,点 , , , , , , 是网格线交点,当船航行到点的位置时,此时与两个灯塔 , 间的角度的大小一定无触礁危险那么,对于 , , , 四个位置,船处于____时,也一定无触礁危险( ) A、位置 B、位置 C、位置 D、位置10. 如图,一根竹竿 , 斜靠在竖直的墙上,点是中点,表示竹竿及在竹竿滑动过程中的情况是( )
A、位置 B、位置 C、位置 D、位置10. 如图,一根竹竿 , 斜靠在竖直的墙上,点是中点,表示竹竿及在竹竿滑动过程中的情况是( ) A、 下滑时,的长度增大 B、上升时,的长度减小 C、只要滑动,端沿墙向下滑动过程中的某个位置,则的长的长度就变化 D、无论怎样滑动,的长度不变11. 如图,直线l是一次函数的图象,且直线l过点 , 则下列结论错误的是( )
A、 下滑时,的长度增大 B、上升时,的长度减小 C、只要滑动,端沿墙向下滑动过程中的某个位置,则的长的长度就变化 D、无论怎样滑动,的长度不变11. 如图,直线l是一次函数的图象,且直线l过点 , 则下列结论错误的是( )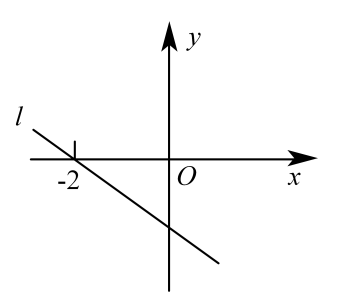 A、 B、直线l过坐标为的点 C、若点 , 在直线上,则 D、12. 如图,ABCD中,AB=22cm,BC=cm,∠A=45°,动点E从A出发, 以2cm/s的速度沿AB向点B运动,动点F从点C出发,以1cm/s的速度沿着CD向D运动,当点E到达点B时,两个点同时停止.则EF的长为10cm时点E的运动时间是( )
A、 B、直线l过坐标为的点 C、若点 , 在直线上,则 D、12. 如图,ABCD中,AB=22cm,BC=cm,∠A=45°,动点E从A出发, 以2cm/s的速度沿AB向点B运动,动点F从点C出发,以1cm/s的速度沿着CD向D运动,当点E到达点B时,两个点同时停止.则EF的长为10cm时点E的运动时间是( )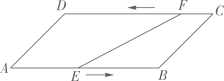 A、6s B、6s或10s C、8s D、8s或12s13. 如图,在▱中,点 , 是对角线上的两个点,且 , 连接 , 求证: .
A、6s B、6s或10s C、8s D、8s或12s13. 如图,在▱中,点 , 是对角线上的两个点,且 , 连接 , 求证: .
证法:如图,在▱中, , ,
.
又 ,
≌ ,
,
,
即 , .

证法:如图,连接交于点 , 连接 , .
在▱中, , .
又 ,
, 即 .
四边形是平行四边形,
.

下列说法错误的是( )
A、证法中证明三角形全等的直接依据是 B、证法中用到了平行四边形的对角线互相平分 C、证法和证法都用到了平行四边形的判定 D、证法和证法都用到了平行四边形的性质14. 甲、乙两地相距千米,一辆货车和一辆轿车分别从甲地开往乙地轿车的平均速度大于货车的平均速度 , 如图线段和折线分别表示两车离甲地的距离单位:千米与时间单位:小时之间的函数关系则下列说法正确的是( ) A、两车同时到达乙地 B、轿车在行驶过程中的平均速度为千米小时 C、货车出发小时后,轿车追上货车 D、两车在前千米的速度相等15. 如图,在平行四边形中, , , , , 分别是边 , 上的动点,连接 , , , 分别是 , 的中点,连接 , 则的最大值与最小值的差为( )
A、两车同时到达乙地 B、轿车在行驶过程中的平均速度为千米小时 C、货车出发小时后,轿车追上货车 D、两车在前千米的速度相等15. 如图,在平行四边形中, , , , , 分别是边 , 上的动点,连接 , , , 分别是 , 的中点,连接 , 则的最大值与最小值的差为( )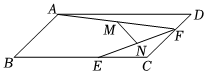 A、 B、 C、 D、16. 如图,中, , , 分别以、、为边在的同侧作正方形、、 , 四块阴影部分的面积分别为、、、则等于( )
A、 B、 C、 D、16. 如图,中, , , 分别以、、为边在的同侧作正方形、、 , 四块阴影部分的面积分别为、、、则等于( )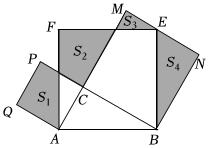 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共3小题,共10.0分)
-
17. 小红在一张菱形纸片中剪掉一个正方形,做成班刊刊头如图所示若菱形的面积为 , 正方形的面积为 , 则这张菱形纸片的边长为 .
 18. 如图,在平面直角坐标系中,矩形的点和点分别落在轴和轴上, , , 直线以每秒个单位长度向下移动,经过 秒该直线可将矩形的面积平分.
18. 如图,在平面直角坐标系中,矩形的点和点分别落在轴和轴上, , , 直线以每秒个单位长度向下移动,经过 秒该直线可将矩形的面积平分. 19. 已知 , 都是实数,为整数,若 , 则称与是关于的一组“平衡数”.
19. 已知 , 都是实数,为整数,若 , 则称与是关于的一组“平衡数”.① 与 是关于的“平衡数”;
② 与 是关于的平衡数;
③ 若 , , 判断与 是或否为关于某数的一组“平衡数”.
三、解答题(本大题共6小题,共57.0分。解答应写出文字说明,证明过程或演算步骤)
-
20. 某校给全体学生推送了“天天跳绳”用来督促学生进行体育锻炼,为了检查学生体育锻炼的效果,从全年级随机抽取了若干名学生进行一分钟跳绳的次数调查统计,一分钟跳绳次数记作 , 并绘制了如下的统计表:
组别
“跳绳次数“次
频率
组内学生的平均“跳绳次数”次
通过体育老师了解到成绩位于等级的学生成绩为:、、、、、、、、、、、;
请根据以上信息回答下列问题:
(1)、本次抽样调查的学生一共有 人;调查的学生“跳绳次数”的中位数是 ;(2)、求该校学生一分钟跳绳次数的平均数;(3)、该校共有学生人,若规定一分钟跳绳次数时为优秀请你估计该校学生一分钟跳绳次数达到优秀的人数.21. 材料阅读:给定三个正整数、、 , 若它们满足 , 则称、、这三个数为“勾股数”例如:, , ; , 即 , 、、这三个数为勾股数.
, , ; , 即 , 、、这三个数为勾股数.
若三角形的三条边、、满足勾股数,即 , 则这个三角形为直角三角形,且、分别为直角的两条邻边如题图所示

根据以上信息,解答下列问题:
(1)、试判断、、是否为勾股数;(2)、若某三角形的三边长分别为、、 , 求其面积;(3)、已知某直角三角形的两边长为和 , 求其周长.22. 如图是个台阶的示意图,每个台阶的高和宽分别是和 , 每个台阶凸出的角的顶点记作为的整数已知点 , 直线:经过点 . (1)、若直线过点 , 求直线的解析式;(2)、试推算出和的数量关系;(3)、若直线使得为的整数这些点分布在它的两侧,每侧各个点,求的取值范围.23. 如图,在平行四边形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)、若直线过点 , 求直线的解析式;(2)、试推算出和的数量关系;(3)、若直线使得为的整数这些点分布在它的两侧,每侧各个点,求的取值范围.23. 如图,在平行四边形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF. (1)、求证:四边形ADFE是矩形;(2)、连接OF,若AD=6,EC=4,∠ABF=60°,求OF的长度.24. 足球世界杯期间,某商店购进、两种品牌的足球进行销售每个品牌足球的销售利润为元、每个品牌足球的销售利润为元.(1)、商店计划购进两种品牌足球共个,设购进品牌足球个,两种足球全部销售完共获利元.
(1)、求证:四边形ADFE是矩形;(2)、连接OF,若AD=6,EC=4,∠ABF=60°,求OF的长度.24. 足球世界杯期间,某商店购进、两种品牌的足球进行销售每个品牌足球的销售利润为元、每个品牌足球的销售利润为元.(1)、商店计划购进两种品牌足球共个,设购进品牌足球个,两种足球全部销售完共获利元.求与之间的函数关系式;不必写的取值范围
若购进品牌足球的个数不少于个,且不超过品牌足球个数的倍,求最大利润为多少;
(2)、在的条件下,该商店对品牌足球以每个优惠元的价格进“双十二”促销活动,品牌售价不变,且全部足球售完后最大利润为元,求出的值.25. 如图,在平面直角坐标系中,点、点分别在轴与轴上,直线的解析式为 , 以线段、为边作平行四边形 .(1)、如图 , 若点的坐标为 , 判断四边形的形状,并说明理由;(2)、如图 , 在的条件下,为边上的动点,点关于直线的对称点是 , 连接 , .当 ▲ 时,点位于线段的垂直平分线上;
连接 , , 设 , 设的延长线交边于点 , 当时,求证: , 并求出此时的值.
