河北省石家庄市长安区2022-2023学年七年级下学期期末数学试卷
试卷更新日期:2023-10-18 类型:期末考试
一、选择题(本大题共16小题,共42.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 如图,的一个外角是( )
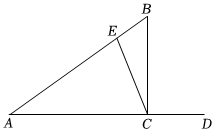 A、 B、 C、 D、2. 若 , 则表示的数是( )A、 B、 C、 D、3. 将不等式的两边同时除以 , 得( )A、 B、 C、 D、4. 下列线段能构成三角形的是( )A、 , , B、 , , C、 , , D、 , ,5. 如图,将沿射线平移得到 , 下列线段的长度能表示平移距离的是( )
A、 B、 C、 D、2. 若 , 则表示的数是( )A、 B、 C、 D、3. 将不等式的两边同时除以 , 得( )A、 B、 C、 D、4. 下列线段能构成三角形的是( )A、 , , B、 , , C、 , , D、 , ,5. 如图,将沿射线平移得到 , 下列线段的长度能表示平移距离的是( )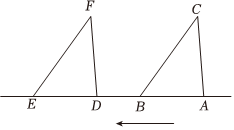 A、 B、 C、 D、6. 将用科学记数法表示成的形式,下列说法正确的是( )A、 , 都是负整数 B、 , 都是正整数 C、是负整数,是正整数 D、是正整数,是负整数7. 如图,将一个直角三角形纸片的直角顶点放在直线上的点处,固定直线 , 当纸片绕着点在直线上方旋转时,与的度数会发生改变,则与( )
A、 B、 C、 D、6. 将用科学记数法表示成的形式,下列说法正确的是( )A、 , 都是负整数 B、 , 都是正整数 C、是负整数,是正整数 D、是正整数,是负整数7. 如图,将一个直角三角形纸片的直角顶点放在直线上的点处,固定直线 , 当纸片绕着点在直线上方旋转时,与的度数会发生改变,则与( ) A、是对顶角 B、互为余角 C、互为邻补角 D、互为补角8. 下面是计算的过程:
A、是对顶角 B、互为余角 C、互为邻补角 D、互为补角8. 下面是计算的过程:解:
步骤、分别是( )
A、合并同类项,同底数幂的乘法 B、幂的乘方,同底数幂的乘法 C、幂的乘方,积的乘方 D、积的乘方,合并同类项9. 下列图形中,一定成立的是( )A、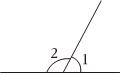 B、
B、 C、
C、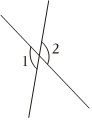 D、
D、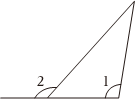 10. 解关于 , 的二元一次方程组 , 由可直接消去未知数 , 则和满足的条件是( )A、 B、 C、 D、11. 在对多项式因式分解的过程中,没有用到的方法有( )A、提公因式 B、平方差公式 C、完全平方公式 D、提公因式12. 将直角三角板按如图所示的方式摆放,其中 , , 若 , 则( )
10. 解关于 , 的二元一次方程组 , 由可直接消去未知数 , 则和满足的条件是( )A、 B、 C、 D、11. 在对多项式因式分解的过程中,没有用到的方法有( )A、提公因式 B、平方差公式 C、完全平方公式 D、提公因式12. 将直角三角板按如图所示的方式摆放,其中 , , 若 , 则( ) A、 B、 C、 D、13. 某超市花费元购进苹果千克,销售中有的正常损耗,为避免亏本其它费用不考虑 , 售价至少定为多少元千克?设售价为元千克,根据题意所列不等式正确的是( )A、 B、 C、 D、14. 定理:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
A、 B、 C、 D、13. 某超市花费元购进苹果千克,销售中有的正常损耗,为避免亏本其它费用不考虑 , 售价至少定为多少元千克?设售价为元千克,根据题意所列不等式正确的是( )A、 B、 C、 D、14. 定理:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.已知:如图,直线 , 被直线所截, .
对说明理由.

方法:
如图,量角器测量所得 ,
对顶角相等 ,
角的度数相等 .
同位角相等,两直线平行 .
方法:
如图,已知 ,
对顶角相等 ,
等量代换 ,
同位角相等,两直线平行 .
下列说法正确的是( )
A、方法只要测量够组内错角进行验证,就能说明该定理的正确性 B、方法用特殊到一般的数学方法说明了该定理的正确性 C、方法用严谨的推理说明了该定理的正确性 D、方法还需说明其他位置的内错角,对该定理的说明才完整15. 小羽制作了如图所示的卡片类,类,类各张,其中 , 两类卡片都是正方形,类卡片是长方形,现要拼一个长为 , 宽为的大长方形,那么所准备的类卡片的张数( ) A、够用,剩余张 B、够用,剩余张 C、不够用,还缺张 D、不够用,还缺张16. 如图,点是射线上一点,且 , 下列结论:
A、够用,剩余张 B、够用,剩余张 C、不够用,还缺张 D、不够用,还缺张16. 如图,点是射线上一点,且 , 下列结论:结论Ⅰ:若是直角三角形,则有 .
结论Ⅱ:当是钝角三角形时,则有 .
下列说法正确的是( )
 A、结论Ⅰ和结论Ⅱ都正确 B、结论Ⅰ和结论Ⅱ都不正确 C、只有结论Ⅰ正确 D、只有结论Ⅱ正确
A、结论Ⅰ和结论Ⅱ都正确 B、结论Ⅰ和结论Ⅱ都不正确 C、只有结论Ⅰ正确 D、只有结论Ⅱ正确二、填空题(本大题共4小题,共12.0分)
-
17. 因式分解: .18. 如图,是的中线,于点 , 于点已知: , , , 则 .
 19. 按如图的运算程序进行运算,当运算到“判断结果是否大于”为一次运算.
19. 按如图的运算程序进行运算,当运算到“判断结果是否大于”为一次运算.
(1)当时,输出的数值是 ;
(2)若该程序只运行了次运算就停止了,则的取值范围为 .
20. 在一个三角形中,如果有一个角是另一个角的倍,我们称这两个角互为“开心角”,这个三角形叫做“开心三角形”例如:在中, , , 则与互为“开心角”,为“开心三角形”.(1)若为开心三角形, , 则这个三角形中最小的内角为 ;
(2)若为开心三角形, , 则这个三角形中最小的内角为
三、解答题(本大题共5小题,共46.0分。解答应写出文字说明,证明过程或演算步骤)
-
21. 解不等式组,并把解集在数轴上表示出来. .
 22. 把下面的推理过程补充完整,并在括号内注明理由.
22. 把下面的推理过程补充完整,并在括号内注明理由.如图,已知 , .
试说明: .

解:已知 ,
又已知 ,
▲ .
23. 已知x,y满足方程组求代数式的值.24. 合肥市琥珀中学计划组织七年级师生举行“春季研学游”活动,活动组织负责人从旅游公司了解到如下租车信息:车型
载客量人辆
租金元辆
校方从实际情况出发,决定租用 , 型客车共辆,且两种车型都要租用租车费用不超过元.
(1)、请问校方最多租用型客车多少辆?(2)、在(1)的条件下,校方根据自愿原则,统计发现共有人参加本次活动,请问合理的租车方案有哪几种?最省钱的租车方式是哪一种?25. 如图 , , 平分 , 点 , , 分别是射线 , , 上的点都不与点重合 , 交于点设 . (1)、如图 , 当时,
(1)、如图 , 当时,求的度数;
若 , 求的值.
(2)、如图 , 若 , 是否存在的值,使得中有两个角相等若存在,直接写出的值;若不存在,说明理由.