河北省石家庄市辛集市2022-2023学年七年级下学期期末数学试卷
试卷更新日期:2023-10-18 类型:期末考试
一、选择题(本大题共16小题,共48.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 在平面直角坐标系中,点落在( )A、第一象限 B、轴正半轴上 C、第二象限 D、轴正半轴上2. 下列调查方式,你认为最合适的是( )A、对某地区饮用水矿物质含量的调查,采用抽样调查方式 B、旅客上飞机前的安全检查,采用抽样调查方式 C、对某班学生的校服尺寸大小的调查,采用抽样调查方式 D、调查某批次汽车的抗撞击能力,采用全面调查方式3. 下列命题是真命题的是( )A、同位角相等 B、内错角相等 C、同旁内角互补 D、邻补角互补4. 已知是二元一次方程的解,又是下列哪个方程的解?( )A、 B、 C、 D、5. 关于的不等式的解集是( )A、 B、 C、 D、6. 下列说法错误的是( )A、的立方根是 B、算术平方根等于本身的数是 , C、 D、的平方根是7. 如图,数轴上,下列各数是无理数且表示的点在线段上的是( )
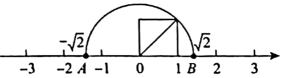 A、0 B、 C、 D、8. 不等式组的解在数轴上表示为( )A、
A、0 B、 C、 D、8. 不等式组的解在数轴上表示为( )A、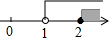 B、
B、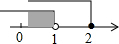 C、
C、 D、
D、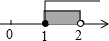 9. 如图是天安门周围的景点分布示意图.在图中,分别以正东,正北方向为轴,轴的正方向建立平面直角坐标系.如果表示景山的点的坐标为 , 表示王府井的点的坐标为 , 则表示人民大会堂的点的坐标为( )
9. 如图是天安门周围的景点分布示意图.在图中,分别以正东,正北方向为轴,轴的正方向建立平面直角坐标系.如果表示景山的点的坐标为 , 表示王府井的点的坐标为 , 则表示人民大会堂的点的坐标为( ) A、 B、 C、 D、10. 蓝天无人机专卖店三月份销售无人机若干架,其中甲种型号无人机架数比总架数的一半多架,乙种型号无人机架数比总架数的少架设销售甲种型号无人机架,乙种型号无人机架,根据题意可列出的方程组是( )A、 B、 C、 D、11. 如图,将线段平移到线段的位置,则的值为( )
A、 B、 C、 D、10. 蓝天无人机专卖店三月份销售无人机若干架,其中甲种型号无人机架数比总架数的一半多架,乙种型号无人机架数比总架数的少架设销售甲种型号无人机架,乙种型号无人机架,根据题意可列出的方程组是( )A、 B、 C、 D、11. 如图,将线段平移到线段的位置,则的值为( )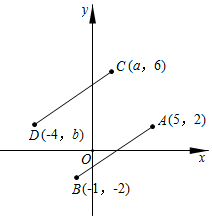 A、 B、 C、 D、12. 老师布置了一项作业,对一个真命题进行证明,下面是小云给出的证明过程:
A、 B、 C、 D、12. 老师布置了一项作业,对一个真命题进行证明,下面是小云给出的证明过程:证明:如图, ,
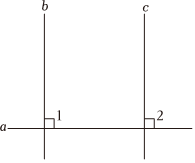
.
,
,
,
.
已知该证明过程是正确的,则证明的真命题是( )
A、在同一平面内,若 , 且 , 则 B、在同一平面内,若 , 且 , 则 C、两直线平行,同位角不相等 D、两直线平行,同位角相等13. 在平面直角坐标系中,点 , , 当线段AB长度最短时,的值为( )A、0 B、1 C、2 D、314. 下面是两球从不同高度自由下落到地面后反弹高度的折线统计图,根据图中信息,在实验数据范围内,以下说法错误的是( )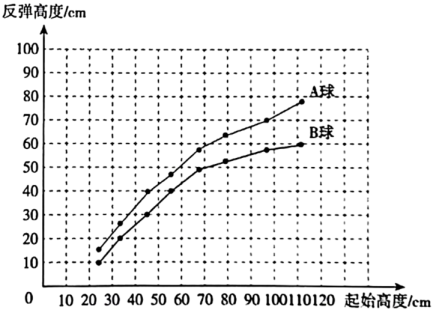 A、球与球相比,球的弹性更大 B、随着起始高度增加,两球的反弹高度也会增加 C、两球的反弹高度均不会超过相应的起始高度 D、将球从68cm的高度自由下落,第二次接触地面后的反弹高度小于40cm15. 已知关于 , 的方程组的解满足 , 则的取值范围是( )A、 B、 C、 D、16. 要得知作业纸上两相交直线、所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案如图和图:
A、球与球相比,球的弹性更大 B、随着起始高度增加,两球的反弹高度也会增加 C、两球的反弹高度均不会超过相应的起始高度 D、将球从68cm的高度自由下落,第二次接触地面后的反弹高度小于40cm15. 已知关于 , 的方程组的解满足 , 则的取值范围是( )A、 B、 C、 D、16. 要得知作业纸上两相交直线、所夹锐角的大小,发现其交点不在作业纸内,无法直接测量.两同学提供了如下间接测量方案如图和图: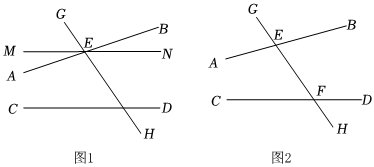
对于方案Ⅰ、Ⅱ,说法正确的是( )
方案Ⅰ:作一直线 , 交、于点 , ;
利用尺规作;
测量的大小即可.
方案Ⅱ:作一直线 , 交、于点 , ;
测量和的大小;
计算即可.
A、Ⅰ可行、Ⅱ不可行 B、Ⅰ不可行、Ⅱ可行 C、Ⅰ、Ⅱ都可行 D、Ⅰ、Ⅱ都不可行二、填空题(本大题共3小题,共9.0分)
-
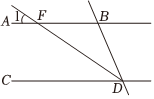
17. 一个正数的平方根分别是与 , 则立方根是 .18. 如图,是的平分线, , , 则的度数为 .
 19. 为美化广场环境要建花坛,一个花坛由四季海棠 、三色堇、蔷薇三种花卉组成,这三种花卉的盆数同时满足以下三个条件:
19. 为美化广场环境要建花坛,一个花坛由四季海棠 、三色堇、蔷薇三种花卉组成,这三种花卉的盆数同时满足以下三个条件:a.三色堇的盆数多于四季海棠的盆数;
b.四季海棠的盆数多于蔷薇的盆数;
c.蔷薇盆数的2倍多于三色堇的盆数.
①若蔷薇的盆数为4,则四季海棠盆数的最大值为:
②一个花坛花盆数量的最小值为 .
三、解答题(本大题共7小题,共63.0分。解答应写出文字说明,证明过程或演算步骤)
-
20.(1)、计算:;(2)、解方程组: .21. 已知不等式与同时成立,求的整数值.22. 补全横线上的内容并在括号中填入适当的理由:
如图, , , ;
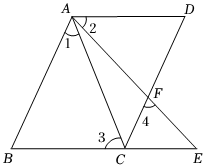
求证: .
证明:已知 ,
已知 ,
即 ▲ .
已知 ,
▲
23. 某初中学校为了解学生每天的睡眠时间单位:小时 , 在全校名学生中随机抽取部分学生进行了一次问卷调查,并将调查结果分为、、、四个组进行统计,根据统计的信息,绘制了如图不完整的频数分布直方图、扇形统计图根据以上信息,解答下列问题: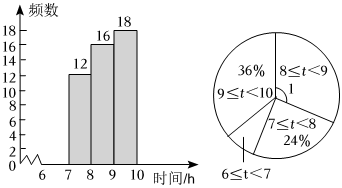 (1)、填空:本次调查中,样本容量为 ▲ ;睡眠时间在范围内的学生占抽取学生的百分比为 ▲ ;在扇形统计图中,对应的圆心角的度数是度 ▲ ;请补全频数分布直方图.(2)、若睡眠时间未达到小时的学生需要加强睡眠管理,则该校全校学生需要加强睡眠管理的学生大约有多少人?24. 某学校在宣传垃圾分类的实践活动中,需印制主题为“做文明有礼中学生,垃圾分类从我做起”的宣传单,其附近两家图文社印制此种宣传单的收费标准如图所示:
(1)、填空:本次调查中,样本容量为 ▲ ;睡眠时间在范围内的学生占抽取学生的百分比为 ▲ ;在扇形统计图中,对应的圆心角的度数是度 ▲ ;请补全频数分布直方图.(2)、若睡眠时间未达到小时的学生需要加强睡眠管理,则该校全校学生需要加强睡眠管理的学生大约有多少人?24. 某学校在宣传垃圾分类的实践活动中,需印制主题为“做文明有礼中学生,垃圾分类从我做起”的宣传单,其附近两家图文社印制此种宣传单的收费标准如图所示: (1)、为达到及时宣传的目的,学校同时在、两家图文社共印制了张宣传单,印制费用共计元,学校在、两家图文社各印制了多少张宣传单(2)、次月,为扩大宣传,学校计划选择家图文社加印一部分宣传单,在印制费用不超过元的前提下,最多可以印制多少张宣传单25. 已知:点C是∠AOB的OA边上一点(点C不与点O重合),点D是∠AOB内部一点,射线CD不与OB相交.
(1)、为达到及时宣传的目的,学校同时在、两家图文社共印制了张宣传单,印制费用共计元,学校在、两家图文社各印制了多少张宣传单(2)、次月,为扩大宣传,学校计划选择家图文社加印一部分宣传单,在印制费用不超过元的前提下,最多可以印制多少张宣传单25. 已知:点C是∠AOB的OA边上一点(点C不与点O重合),点D是∠AOB内部一点,射线CD不与OB相交.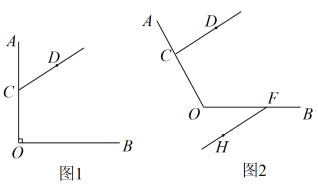 (1)、如图1,∠AOB=90°,∠OCD=120°,过点O作射线OE,使得OE//CD.(其中点E在∠AOB内部).
(1)、如图1,∠AOB=90°,∠OCD=120°,过点O作射线OE,使得OE//CD.(其中点E在∠AOB内部).①依据题意,补全图1;
②直接写出∠BOE的度数.
(2)、如图2,点F是射线OB上一点,且点F不与点O重合,当时,过点F作射线FH,使得FH//CD(其中点H在∠AOB的外部),用含的代数式表示∠OCD与∠BFH的数量关系,并证明.26. 定义:以二元一次方程的解为坐标的点的全体叫做这个方程的图象,这些点叫做该图象的关联点.(1)、在;;三点中,是方程图象的关联点有 ;填序号(2)、已知 , 两点是方程图象的关联点, , 两点是方程图象的关联点若点在轴上,点在轴上,求四边形的面积.(3)、若 , , 三点是二元一次方程图象的关联点,探究与的大小.