山东省淄博市2023年中考数学真题
试卷更新日期:2023-10-18 类型:中考真卷
一、单选题
-
1. 的运算结果等于( )A、3 B、 C、 D、2. 在如图所示的几何体中,其主视图、左视图和俯视图完全相同的是( )A、
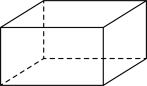 B、
B、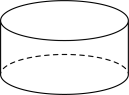 C、
C、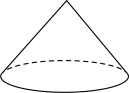 D、
D、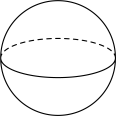 3. 下列计算结果正确的是( )A、 B、 C、 D、4. 将含角的直角三角板按如图所示放置到一组平行线中,若 , 则等于( )
3. 下列计算结果正确的是( )A、 B、 C、 D、4. 将含角的直角三角板按如图所示放置到一组平行线中,若 , 则等于( ) A、 B、 C、 D、5. 已知是方程的解,那么实数的值为( )A、 B、2 C、 D、46. 下列函数图象中,能反映的值始终随值的增大而增大的是( )A、
A、 B、 C、 D、5. 已知是方程的解,那么实数的值为( )A、 B、2 C、 D、46. 下列函数图象中,能反映的值始终随值的增大而增大的是( )A、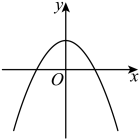 B、
B、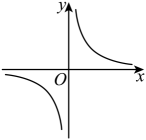 C、
C、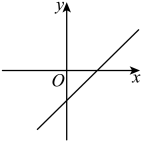 D、
D、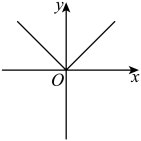 7. 为贯彻落实习近平总书记关于黄河流域生态保护和高质量发展的重要讲话精神,某学校组织初一、初二两个年级学生到黄河岸边开展植树造林活动.已知初一植树棵与初二植树棵所用的时间相同,两个年级平均每小时共植树棵.求初一年级平均每小时植树多少棵?设初一年级平均每小时植树棵,则下面所列方程中正确的是( )A、 B、 C、 D、8. “敬老爱老”是中华民族的优秀传统美德.小刚、小强计划利用暑期从 , , 三处养老服务中心中,随机选择一处参加志愿服务活动,则两人恰好选到同一处的概率是( )A、 B、 C、 D、9. 如图,是的内接三角形, , , 是边上一点,连接并延长交于点 . 若 , , 则的半径为( )
7. 为贯彻落实习近平总书记关于黄河流域生态保护和高质量发展的重要讲话精神,某学校组织初一、初二两个年级学生到黄河岸边开展植树造林活动.已知初一植树棵与初二植树棵所用的时间相同,两个年级平均每小时共植树棵.求初一年级平均每小时植树多少棵?设初一年级平均每小时植树棵,则下面所列方程中正确的是( )A、 B、 C、 D、8. “敬老爱老”是中华民族的优秀传统美德.小刚、小强计划利用暑期从 , , 三处养老服务中心中,随机选择一处参加志愿服务活动,则两人恰好选到同一处的概率是( )A、 B、 C、 D、9. 如图,是的内接三角形, , , 是边上一点,连接并延长交于点 . 若 , , 则的半径为( )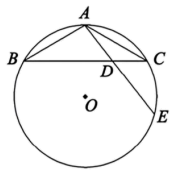 A、 B、 C、 D、10. 勾股定理的证明方法丰富多样,其中我国古代数学家赵爽利用“弦图”的证明简明、直观,是世界公认最巧妙的方法.“赵爽弦图”已成为我国古代数学成就的一个重要标志,千百年来倍受人们的喜爱.小亮在如图所示的“赵爽弦图”中,连接 , . 若正方形与的边长之比为 , 则等于( )
A、 B、 C、 D、10. 勾股定理的证明方法丰富多样,其中我国古代数学家赵爽利用“弦图”的证明简明、直观,是世界公认最巧妙的方法.“赵爽弦图”已成为我国古代数学成就的一个重要标志,千百年来倍受人们的喜爱.小亮在如图所示的“赵爽弦图”中,连接 , . 若正方形与的边长之比为 , 则等于( )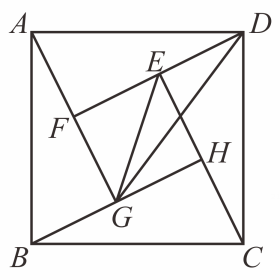 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
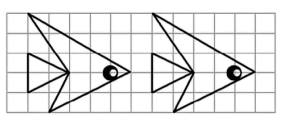
11. 25的平方根是 .12. 在边长为1的正方形网格中,右边的“小鱼”图案是由左边的图案经过一次平移得到的,则平移的距离是 .
 13. 分解因式:2a2﹣8b2=14. 如图,在直线:上方的双曲线上有一个动点 , 过点作轴的垂线,交直线于点 , 连接 , , 则面积的最大值是 .
13. 分解因式:2a2﹣8b2=14. 如图,在直线:上方的双曲线上有一个动点 , 过点作轴的垂线,交直线于点 , 连接 , , 则面积的最大值是 .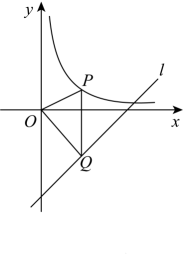 15. 如图,与斜坡垂直的太阳光线照射立柱(与水平地面垂直)形成的影子,一部分落在地面上,另一部分落在斜坡上.若米,米,斜坡的坡角 , 则立柱的高为米(结果精确到米).
15. 如图,与斜坡垂直的太阳光线照射立柱(与水平地面垂直)形成的影子,一部分落在地面上,另一部分落在斜坡上.若米,米,斜坡的坡角 , 则立柱的高为米(结果精确到米).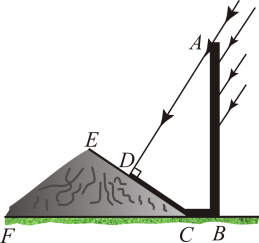

科学计算器按键顺序
计算结果(已取近似值)



三、解答题
-
16. 先化简,再求值: , 其中 , .17. 如图,在中, , 分别是边和上的点,连接 , , 且 . 求证:
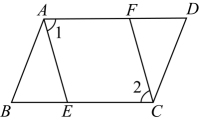 (1)、;(2)、 .18. 若实数 , 分别满足下列条件:
(1)、;(2)、 .18. 若实数 , 分别满足下列条件:;(2) . 试判断点所在的象限
19. 举世瞩目的中国共产党第二十次全国代表大会于2022年10月在北京成功召开.为弘扬党的二十大精神,某学校举办了“学习二十大,奋进新征程”的知识竞赛活动.赛后随机抽取了部分学生的成绩(满分:100分),分为 , , , 四组,绘制了如下不完整的统计图表:组别
成绩(:分)
频数
20
60
学生成绩频数分布直方图
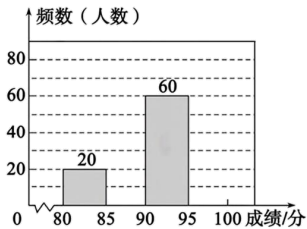
学生成绩扇形统计图
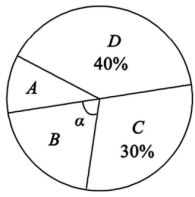
根据以上信息,解答以下问题:
(1)、直接写出统计表中的 , ;(2)、学生成绩数据的中位数落在组内;在学生成绩扇形统计图中,组对应的扇形圆心角是度;(3)、将上面的学生成绩频数分布直方图补充完整;(4)、若全校有1500名学生参加了这次竞赛,请估计成绩高于90分的学生人数.20. 如图,直线与双曲线相交于点 , .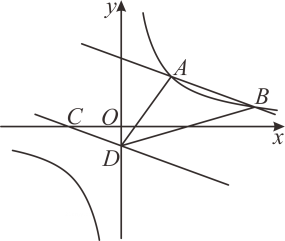 (1)、求双曲线及直线对应的函数表达式;(2)、将直线向下平移至处,其中点 , 点在轴上.连接 , , 求的面积;(3)、请直接写出关于的不等式的解集.21. 某古镇为发展旅游产业,吸引更多的游客前往游览,助力乡村振兴,决定在“五一”期间对团队*旅游实行门票特价优惠活动,价格如下表:
(1)、求双曲线及直线对应的函数表达式;(2)、将直线向下平移至处,其中点 , 点在轴上.连接 , , 求的面积;(3)、请直接写出关于的不等式的解集.21. 某古镇为发展旅游产业,吸引更多的游客前往游览,助力乡村振兴,决定在“五一”期间对团队*旅游实行门票特价优惠活动,价格如下表:购票人数(人)
每人门票价(元)
60
50
40
*题中的团队人数均不少于10人
现有甲、乙两个团队共102人,计划利用“五一”假期到该古镇旅游,其中甲团队不足50人,乙团队多于50人.
(1)、如果两个团队分别购票,一共应付5580元,问甲、乙团队各有多少人?(2)、如果两个团队联合起来作为一个“大团队”购票,比两个团队各自购票节省的费用不少于1200元,问甲团队最少多少人?22. 在数学综合与实践活动课上,小红以“矩形的旋转”为主题开展探究活动.(1)、操作判断小红将两个完全相同的矩形纸片和拼成“L”形图案,如图①.
试判断:的形状为 .
 (2)、深入探究
(2)、深入探究小红在保持矩形不动的条件下,将矩形绕点旋转,若 , .
探究一:当点恰好落在的延长线上时,设与相交于点 , 如图②.求的面积.
探究二:连接 , 取的中点 , 连接 , 如图③.
求线段长度的最大值和最小值.
 23. 如图,一条抛物线经过的三个顶点,其中为坐标原点,点 , 点在第一象限内,对称轴是直线 , 且的面积为18
23. 如图,一条抛物线经过的三个顶点,其中为坐标原点,点 , 点在第一象限内,对称轴是直线 , 且的面积为18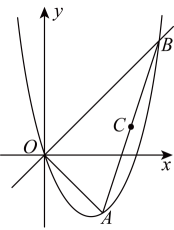 (1)、求该抛物线对应的函数表达式;(2)、求点的坐标;(3)、设为线段的中点,为直线上的一个动点,连接 , , 将沿翻折,点的对应点为 . 问是否存在点 , 使得以 , , , 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点的坐标;若不存在,请说明理由.
(1)、求该抛物线对应的函数表达式;(2)、求点的坐标;(3)、设为线段的中点,为直线上的一个动点,连接 , , 将沿翻折,点的对应点为 . 问是否存在点 , 使得以 , , , 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点的坐标;若不存在,请说明理由.