吉林省长春市108中2023-2024学年九年级上学期第一次月考数学试卷
试卷更新日期:2023-10-18 类型:月考试卷
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 二次根式有意义,则的取值范围是( )A、 B、 C、 D、2. 下列二次根式中与 是同类二次根式的是( )A、 B、 C、 D、3. 用配方法解方程下列配方正确的是( )A、 B、 C、 D、4. 二道区为发展教育事业,加强了对教育经费的投入,年投入万元,预计年投入万元设教育经费的年平均增长率为 , 根据题意,下面所列方程正确的是( )A、 B、 C、 D、5. 如图,直线 , 直线分别交 , , 于点 , , , 直线分别交 , , 于点 , , 若 , , 则的长为( )
 A、 B、 C、 D、6. 如图,点为的重心,过点作 , 分别交、于点、 , 则与的周长之比为( )
A、 B、 C、 D、6. 如图,点为的重心,过点作 , 分别交、于点、 , 则与的周长之比为( ) A、: B、: C、: D、:7. 西周时期,丞相周公且设置过一种通过测定日影长度来确定时间的仪器,称为圭表如图是一个根据北京的地理位置设计的圭表,其中,立柱高为已知,冬至时北京的正午日光入射角约为 , 则立柱根部与圭表的冬至线的距离即的长约为( )
A、: B、: C、: D、:7. 西周时期,丞相周公且设置过一种通过测定日影长度来确定时间的仪器,称为圭表如图是一个根据北京的地理位置设计的圭表,其中,立柱高为已知,冬至时北京的正午日光入射角约为 , 则立柱根部与圭表的冬至线的距离即的长约为( ) A、 B、 C、 D、8. 已知是反比例函数图象上一点,点的坐标为 , 是轴正半轴上一点,且 , :: , 那么点的纵坐标为( )
A、 B、 C、 D、8. 已知是反比例函数图象上一点,点的坐标为 , 是轴正半轴上一点,且 , :: , 那么点的纵坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共18.0分)
-
9. 计算: =
10. 关于的一元二次方程有两个不相等的实数根,则的取值范围为 .11. 如图,河坝横断面迎水坡的坡度为 , 坝高 , 则的长度为 . 12. 如图,在的正方形网格中,每个小正方形的边长都是 , 的顶点都在这些小正方形的顶点上,则的值为 .
12. 如图,在的正方形网格中,每个小正方形的边长都是 , 的顶点都在这些小正方形的顶点上,则的值为 . 13. 如图,在平面直角坐标系中,等腰直角是等腰直角以原点为位似中心的位似图形,且位似比为: , 点 , , 在 , 则点坐标为 .
13. 如图,在平面直角坐标系中,等腰直角是等腰直角以原点为位似中心的位似图形,且位似比为: , 点 , , 在 , 则点坐标为 . 14. 如图,点在矩形的边上,将沿翻折,点恰好落在边上的点处,若 , , 则的长为 .
14. 如图,点在矩形的边上,将沿翻折,点恰好落在边上的点处,若 , , 则的长为 .
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 解方程: .16.
计算: .17.
图、图均是的正方形网格,每个小正方形的边长均为 , 每个小正方形的顶点称为格点,的顶点均在格点上只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留适当的作图痕迹.(1)、在图中的线段上找一点 , 连接 , 使 . (2)、在图中的线段上找一点 , 连接 , 使 .(3)、在图中的线段上找一点 , 连接 , 使 .18.
(2)、在图中的线段上找一点 , 连接 , 使 .(3)、在图中的线段上找一点 , 连接 , 使 .18.
长泰大桥是长春市最高的双塔斜拉式高架桥,大桥属于双塔双索面混凝土特大斜拉桥桥型,图是大桥的实物图,图是大桥的示意图假设你站在桥上点处测得拉索与水平桥面的夹角是 , 点处距离大桥立柱底端的距离为米,已知大桥立柱上点距立柱顶端点的距离为米,求大桥立柱的高结果精确到米参考数据: , , 19.
19.
如图,是矩形的边上的一点,于点 , , , . (1)、求证:∽ .(2)、计算点到直线的距离为 .20.
(1)、求证:∽ .(2)、计算点到直线的距离为 .20.
小林同学从家出发,步行到离家米的劳动公园散步,速度为米分钟;分钟后哥哥也从家出发沿着同一路线骑自行车到公园,哥哥到达公园后立即以原速原路返回家中,哥哥返回家中时,小林刚好到达公园,两人离家的距离米与小林出发长的时间分钟的函数关系如图所示. (1)、求哥哥返回家的过程中与之间的函数关系式.(2)、小林出发 分钟与哥哥第二次相遇.21.
(1)、求哥哥返回家的过程中与之间的函数关系式.(2)、小林出发 分钟与哥哥第二次相遇.21.
阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如善于思考的小明进行了以下探索:设 , 其中、、、均为整数 , 则有 , , 这样小明就找到了一种把类似的式子化为平方式的方法请你仿照小明的方法探索并解决下列问题:(1)、当、、、均为整数时,若 , 用含、的式子分别表示、 , 得: , .(2)、利用所探索的结论,找一组正整数、、、 , 填空: .(3)、若 , 且、、均为正整数,求的值.22.
【教材呈现】如图是华师版九年级上册数学教材第页的部分内容.猜想:如图,在中,点、分别是与的中点根据画出的图形,可以猜想: , 且对此,我们可以用演绎推理给出证明.
 (1)、【定理证明】请根据教材内容,结合图 , 写出证明过程.(2)、【定理应用】如图 , 在中, , 平分交于点 , 点为的中点,连接 , 过点作交的延长线于点求证:四边形是平行四边形.(3)、【拓展提升】如图 , 中, , 于点 , 是的中点, , 则 .23.
(1)、【定理证明】请根据教材内容,结合图 , 写出证明过程.(2)、【定理应用】如图 , 在中, , 平分交于点 , 点为的中点,连接 , 过点作交的延长线于点求证:四边形是平行四边形.(3)、【拓展提升】如图 , 中, , 于点 , 是的中点, , 则 .23.
如图 , 在中, , , , 点为边的中点动点从点出发,沿折线向终点运动,点在边上以每秒个单位长度的速度运动,在边上以每秒个单位长度的速度运动,在点运动的过程中,过点作的平行线,过点作的平行线,两条平行线相交于点点不与点、点重合,设点的运动时间为秒..
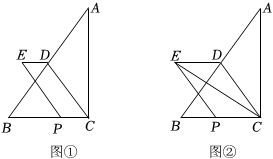 (1)、CB= .(2)、用含的代数式直接表示的长.(3)、当四边形是轴对称图形时,求出的值.(4)、连接 , 如图 , 当将的面积分成:两部分时,直接写出的值.
(1)、CB= .(2)、用含的代数式直接表示的长.(3)、当四边形是轴对称图形时,求出的值.(4)、连接 , 如图 , 当将的面积分成:两部分时,直接写出的值.