河北省保定市高碑店市2023-2024学年八年级上学期数学月考考试试卷

试卷更新日期：2023-10-18 类型：月考试卷

进入出卷网下载

一、选择题（本大题共16个小题，共38分．1~6小题各3分，7~16小题各2分．在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 下列四个实数中，最小的数是（　　）

A、-2 B、0 C、-1 D、 $- \sqrt{5}$

查看试题解析
2. 下列各数中，是无理数的是（　　）

A、 $\frac{1}{3}$ B、3.14 C、 $\frac{π}{2}$ D、0

查看试题解析
3. 下列运算错误的是（　　）

A、 $\sqrt{- 4} = - 2$ B、 $\sqrt{16} = 4$ C、 $\sqrt[3]{- 8} = - 2$ D、 $\sqrt{{(- 3)}^{2}} = 3$

查看试题解析
4. 在 $△ A B C$ 中， $∠ C = 90 °$ ， $A B = 10$ ， $A C = 6$ ，则BC的长为（　　）

A、6 B、8 C、10 D、12

查看试题解析
5. 如图，在数轴上点 $A^{'}$ 表示的实数是（　　）

A、 $- \sqrt{5}$ B、 $- \sqrt{3}$ C、-2 D、 $\sqrt{5}$

查看试题解析
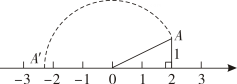6. 如图，小逸家的房门左下角受潮了，他想检测房门是否变形，准备采用如下方法：先测量门的边AB和BC的长，再测量点A和点C间的距离，由此可推断 $∠ B$ 是否为直角，这样做的依据是（　　）

A、勾股定理 B、三角形内角和定理 C、勾股定理的逆定理 D、直角三角形的两锐角互余

查看试题解析
7. 若使算式 $(- 2) ◯ (- 3)$ 的运算结果最小，“ $◯$ ”表示的运算符号是（　　）

A、+ B、- C、× D、÷

查看试题解析
8. 估计 $\sqrt{23}$ 的值在（）

A、 $3$ 和 $4$ 之间 B、 $4$ 和 $5$ 之间 C、 $5$ 和6之间 D、6和 $7$ 之间

查看试题解析
9. 若 $| - \sqrt{3} + * | = * - \sqrt{3}$ ，则“*”代表的数可以是（　　）

A、-2 B、 $- \sqrt{3}$ C、1 D、2

查看试题解析
10. 为了证明数轴上的点可以表示无理数，老师给学生设计了如下材料：如图，直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上一点由原点（记为点O）到达点A ，点A对应的数是（　　）

A、 $π$ B、3.14 C、 $- π$ D、-3.14

查看试题解析
11. 一个数的两个平方根分别是2a+1与-3a+2，则a的值是（）

A、-1 B、1 C、-3 D、3

查看试题解析
12. 下列说法正确的是（　　）

A、 $\sqrt{16}$ 的平方根是 $\pm 4$ B、无限小数是无理数 C、数轴上的点对应的数不是整数就是分数 D、若a ， b ， c为一组勾股数，则2a ， 2b ， 2c仍是一组勾股数

查看试题解析
13. 已知一个三角形的三条边长之比为3：4：5，且三角形的周长为24cm，则三角形的面积为（　　）

A、 $6 c m^{2}$ B、 $12 c m^{2}$ C、 $24 c m^{2}$ D、 $48 c m^{2}$

查看试题解析
14. 实数a ， b ， c在数轴上的对应点的位置如图所示，如果 $a + c = 0$ ，那么下列结论正确的是（　　）

A、 $b < 0$ B、 $a < - b$ C、 $a b > 0$ D、 $b - c > 0$

查看试题解析
15. 如图，所有阴影部分的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C的面积依次为6、10、7，则正方形D的面积为（　　）

A、11 B、16 C、17 D、23

查看试题解析
16. 勾股定理是人类数学文化的一颗璀璨明珠，是用代数思想解决几何问题最重要的工具，也是数形结合的纽带之一．如图，当秋千静止时，踏板离地的垂直高度 $B E = 1 m$ ，将它往前推4m至C处时（即水平距离 $C D = 4 m$ ），踏板离地的垂直高度 $C F = 3 m$ ，它的绳索始终拉直，则绳索AC的长是（　　）

A、4m B、5m C、6m D、8m

查看试题解析

二、填空题（本大题共3个小题，共10分．17小题2分，18~19小题各4分，每空2分）

17. 2的相反数是．

查看试题解析
18. 按如图所示的程序框图进行计算，若输入x的值为3时，则输出结果为；若输入x的值为16时，则输出结果为．

查看试题解析
19. 如图，某小区有一块四边形空地ABCD ，为了美化小区环境，现计划在空地上铺上草坪，其中 $∠ B = 90 °$ ， $A B = 3 m$ ， $B C = 4 m$ ， $C D = 12 m$ ， $A D = 13 m$ ．

(1)、连接AC ，则 $A C =$ m．

(2)、这块草坪的面积为 $m^{2}$ ．

查看试题解析

三、解答题（本大题共7个小题，共72分．解答应写出文字说明、证明过程或演算步骤）

20. 计算： $\sqrt[3]{27} - \sqrt{{(- 2)}^{2}}$ ．

查看试题解析
21. 已知 $5 a + 3$ 的立方根是2， $3 b + 1$ 的算术平方根是5，求 $a + b$ 的平方根．

查看试题解析
22. 《九章算术》是我国古代最重要的数学著作之一，在“勾股”章中记载了一道“折竹抵地”问题：“今有竹高丈，末折抵地，去本三尺，问折者高几何？”翻译如下：如图，有一根竹子高一丈，现在A处折断，竹梢落在地面的B处，B与竹根部C相距3尺，求折断点A与地面的高度AC ．（注：1丈=10尺）

查看试题解析
23. 如图，这是一个棱长为1cm的正方体空盒子（盒子表面厚度忽略不计）．

(1)、盒子外有一只蚂蚁从点A沿表面爬到相对的点B ，求蚂蚁爬行的最短路程．

(2)、盒子内有一只飞虫从点A飞到相对的点B ，求飞虫飞行的最短路程．

查看试题解析
24. 一只蚂蚁从点A沿数轴向左爬了2个单位长度到达点B ，点A表示 $\sqrt{3}$ ，设点B所表示的数为m ．

(1)、求 $| m + 1 | + | m - 1 |$ 的值．

(2)、在数轴上还有C、D两点分别表示实数C、d ，且满足 $\sqrt{c + 3} + | d - 9 | = 0$ ，求cd的立方根．

查看试题解析
25. 如图，在 $△ A B C$ 中， $A C = 6 c m$ ， $B C = 8 c m$ ， $A B = 10 c m$ ， AB的垂直平分线交AB于点D ，交BC于点E ．

(1)、试说明 $△ A B C$ 为直角三角形．

(2)、求CE的长．

查看试题解析
26. 我们把对角线互相垂直的四边形称为“垂美四边形”．如图1，已知四边形ABCD ， $A C ⊥ B D$ ，像这样的四边形称为“垂美四边形”．

图1 图2 图3

(1)、探索证明
如图1，设 $A B = a$ ， $B C = b$ ， $C D = c$ ， $A D = d$ ，猜想 $a^{2}$ ， $b^{2}$ ， $c^{2}$ ， $d^{2}$ 之间的关系，用等式表示出来，并说明你的理由．

(2)、变式思考
如图2，BD ， CE是 $△ A B C$ 的中线， $B D ⊥ C E$ ，垂足为O ， $B C = 2 D E$ ，设 $B C = m$ ， $A C = n$ ， $A B = k$

，请用一个等式把 $m^{2}$ ， $n^{2}$ ， $k^{2}$ 三者之间的数量关系表示出来：．

(3)、拓展应用
如图3，在长方形ABCD中，E为AD的中点，若四边形ABCE为“垂美四边形”，且 $B C = 2$ ，求AB的长．

查看试题解析