湖南省长沙市四校联考2023-2024年度九年级上学期数学月考考试试卷（10月）

试卷更新日期：2023-10-18 类型：月考试卷

进入出卷网下载

一、选择题（本题共10小题，每小题3分，共30分）

1. 下列几何图形既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 据统计，国庆小长假全国各大景点共接待游客约为82600000人次，数据82600000用科学记数法表示为（　　）

A、0.826×10⁶ B、8.26×10⁷ C、82.6×10⁶ D、8.26×10⁸

查看试题解析
3. 已知一组数据 5，4，3，6，7，则这组数据的平均数与中位数分别为（）.

A、7，5 B、5，7 C、5，6 D、5，5

查看试题解析
4. 如图，DE是△ABC的中位线，若BC=8，则DE的长是（）

A、3 B、4 C、5 D、6

查看试题解析
5. 直线 $y = k x + b$ 过点 $A (- 3 ， y_{1}^{}) ， B (4 ， y_{2}^{})$ ，若 $k$ ＜0，则 $y_{1}$ 与 $y_{2}$ 大小关系为（）.

A、y₁＞y₂ B、y₁<y₂ C、y₁=y₂ D、不能确定

查看试题解析
6. 已知点A(a ， 1)与B(5，b)关于原点对称，则a ， b的值分别为（）.

A、5， -1 B、5，1 C、-5，1 D、-5，-1

查看试题解析
7. 已知关于 $x$ 的一元二次方程 $x_{}^{2} - 2 x - 9 = 0$ ，则该方程根的情况是（）.

A、有两个相等的实数根 B、有两个不相等的实数根 C、有一个实数根 D、无实数根

查看试题解析
8. 如图，已知A（1，3），将线段OA绕原点O顺时针旋转90°后得到OA′，则OA′的长度是（）

A、 $\sqrt{10}$ B、3 C、2 $\sqrt{2}$ D、1

查看试题解析
9. 参加一次足球联赛的每两队之间都进行一场比赛，共比赛50场比赛，设参加比赛共有 $x$ 个队，根据题意，所列方程为（）.

A、 $x (x + 1) = 50$ B、 $\frac{x (x + 1)}{2} = 50$ C、 $x (x - 1) = 50$ D、 $\frac{x (x - 1)}{2} = 50$

查看试题解析
10. 已知二次函数y＝ax²＋bx＋c的图象如图所示，顶点为(－1，0)，下列结论：
①abc＜0；②b²－4ac＝0；③2a－b=0；④4a－2b＋c＞0．
其中正确结论的个数是(　　)

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本题共6小题，每小题3分，共18分）

11. 因式分解： $a^{2} - 9 =$ ．

查看试题解析
12. 一次函数 $y = - 3 x + 5$ 的图象不经过第象限.

查看试题解析
13. 一个等腰三角形的两边长分别为方程 $x_{}^{2} - 8 x + 15 = 0$ 的两根，则该等腰三角形的周长为.

查看试题解析
14. 二次函数 $y = x_{}^{2}$ 的图象向右平移3个单位长度，再向上平移4个单位长度所得图象对应函数解析式为.

查看试题解析
15. 如图，在菱形ABCD中，对角线AC与BD交于点O ，过点A作AH⊥BC ，垂直为H点，已知 BD=8，S_菱形_ABCD=24，则AH =.

查看试题解析
16. 如图，在正方形 $A B C D$ 中，点E是边 $B C$ 上的一点，点F在边 $C D$ 的延长线上，且 $B E = D F$ ，连接 $E F$ 交边 $A D$ 于点G．过点A作 $A N ⊥ E F$ ，垂足为点M，交边 $C D$ 于点N．若 $B E = 5 ， C N = 8$ ，则线段 $A B$ 的长为．

查看试题解析

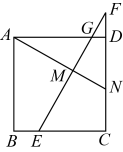
三、简答题（本题共9小题，共72分）

17. 计算： $| - 2 | + {(\sqrt{2} - 1)}^{0} - (- 5) - {(\frac{1}{3})}^{- 1}$

查看试题解析
18. 解方程：

(1)、2x²－4x＝0

(2)、x²－6x－6＝0

查看试题解析
19. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(-2，1)，B(-4，5)，C(-5，2)．

(1)、已知△ABC与△A₁B₁C₁关于原点O成中心对称，请画出△A₁B₁C₁ ，并写出A₁、B₁、C₁三点的坐标；

(2)、求出△A₁B₁C₁的面积．

查看试题解析
20. 为了解学校九年级男生的体能情况，体育老师随机抽取部分男生进行引体向上测试，并对成绩进行了统计，绘制成图1和图2尚不完整的统计图.

(1)、本次抽测的男生共有人，抽测成绩的众数是；

(2)、请你将图(2)的统计图补充完整；

(3)、求这组数据的平均数和中位数；

(4)、若规定引体向上5次以上（含5次）为体能达标，则该校600名九年级男生中，估计有多少人体能达标？

查看试题解析
21. 已知抛物线的顶点为 A (1，-4)，且过点 B(3，0)．

(1)、求二次函数解析式；

(2)、当y>0时，求x的范围；

(3)、当 -1<x<2时，求y的范围.

查看试题解析
22. 随旅游业的快速发展，外来游客对住宿的需求明显增大，某宾馆拥有的床位数不断增加．

(1)、该宾馆床位数从2021年底的200个增长到2023年底的288个，求该宾馆这两年（从2021年底到2023年底）拥有的床位数的年平均增长率；

(2)、该宾馆打算向游客出售了一款纪念工艺品，每件成本50元，为了合理定价，现投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，若销售单价每降低1元，每天就可多售出5件。若该馆想要每天的销售利润达到4000元，且销量尽可能大，应该如何定价？

查看试题解析
23. 在Rt△ABC中，∠ABC＝90°，∠ACB＝30°，将△ABC绕点C顺时针旋转一定的角度α得到△DEC ，点A、B的对应点分别是D、E ．

(1)、当点E恰好在AC上时，如图1，求∠ADE的大小；

(2)、若α＝60°时，点F是AC中点，如图2，求证：四边形BEDF是平行四边形．

查看试题解析
24. 定义：当 $x$ 取任意实数，函数值始终不小于一个常数时，称这个函数为“恒心函数”，这个常数称为“恒心值”.

(1)、判断：函数 $y = x_{}^{2} + 2 x + 2$ 是否为“恒心函数”，如果是，求出此时的“恒心值”，如果不是，请说明理由；

(2)、已知“恒心函数” $y = 3 | a x_{}^{2} + b x + c | + 2$
①当 $a > 0 ， c < 0$ 时，此时的恒心值为；
②若三个整数 $a 、 b 、 c$ 的和为12，且 $\frac{b}{a} = \frac{c}{b}$ ，求 $a$ 的最大值与最小值，并求出此时相应的 $b 、 c$ 的值；

(3)、“恒心函数” $y = a x_{}^{2} + b x + c (b > a)$ 的恒心值为0，且 $\frac{a + b + c}{a + b} > m$ 恒成立，求 $m$ 的取值范围.

查看试题解析
25. 已知抛物线与x轴交于A(-1，0)、C(3，0)，与 $y$ 轴交于点B（0，-3）.

(1)、求抛物线对应的函数解析式；

(2)、在 $x$ 轴上是否存在点P ，使△PBC为等腰三角形？若存在，求出P点坐标；若不存在，请说明理由；

(3)、点M为抛物线上一动点，在直线BC上是否存在点Q ，使以点O、B、Q、M为顶点的四边形为平行四边形？若存在，求出Q点的坐标；若不存在，请说明理由.

查看试题解析