2023-2024学年高中数学人教A版(2019)高二(上)期中测试卷6
试卷更新日期:2023-10-18 类型:期中考试
一、选择题
-
1. 若 , , , 则的形状是( )A、不等边锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形2. 如图,直线的倾斜角为( )
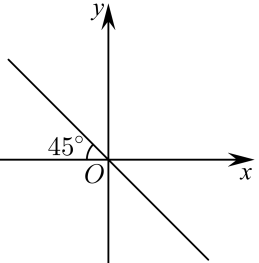 A、 B、 C、 D、3. 已知圆C: , 则圆C的圆心和半径为( )A、圆心 , 半径 B、圆心 , 半径 C、圆心 , 半径 D、圆心 , 半径4. 直线与圆交于A,B两点,则( )A、2 B、 C、4 D、5. 如图,在一个的二面角的棱上有两个点 , , , 在这个二面角的两个面内,并且都垂直于棱 , 且 , , 则的长为( )
A、 B、 C、 D、3. 已知圆C: , 则圆C的圆心和半径为( )A、圆心 , 半径 B、圆心 , 半径 C、圆心 , 半径 D、圆心 , 半径4. 直线与圆交于A,B两点,则( )A、2 B、 C、4 D、5. 如图,在一个的二面角的棱上有两个点 , , , 在这个二面角的两个面内,并且都垂直于棱 , 且 , , 则的长为( ) A、 B、 C、 D、6. 直线的方程为 , 则( )A、的斜率为 B、在轴上的截距为6 C、的截距式为 D、的倾斜角为锐角7. 已知点分别是双曲线的左右两焦点,过点的直线与双曲线的左右两支分别交于两点,若是以为顶角的等腰三角形,其中 , 则双曲线离心率的取值范围为( )A、 B、 C、 D、8. 已知O为椭圆C的中心,F为C的一个焦点, , 经过M的直线与C的一个交点为N,若△MNF是正三角形,则C的离心率为( )A、 B、 C、 D、9. 已知抛物线 , 焦点为F,准线为l,过F的直线交C于A,B两点,过B作l的垂线交l于点D,若的面积为 , 则( )A、3 B、 C、2 D、
A、 B、 C、 D、6. 直线的方程为 , 则( )A、的斜率为 B、在轴上的截距为6 C、的截距式为 D、的倾斜角为锐角7. 已知点分别是双曲线的左右两焦点,过点的直线与双曲线的左右两支分别交于两点,若是以为顶角的等腰三角形,其中 , 则双曲线离心率的取值范围为( )A、 B、 C、 D、8. 已知O为椭圆C的中心,F为C的一个焦点, , 经过M的直线与C的一个交点为N,若△MNF是正三角形,则C的离心率为( )A、 B、 C、 D、9. 已知抛物线 , 焦点为F,准线为l,过F的直线交C于A,B两点,过B作l的垂线交l于点D,若的面积为 , 则( )A、3 B、 C、2 D、二、多项选择题
-
10. 在三维空间中,定义向量的外积: 叫做向量 与 的外积,它是一个向量,满足下列两个条件:① , ,且 , 和 构成右手系(即三个向量的方向依次与右手的拇指、食指、中指的指向一致,如图所示):② 的模 ( 表示向量 , 的夹角)在正方体 中,有以下四个结论,正确的有( )
 A、 B、 C、 共线 D、 与正方体表面积的数值相等11. 下列说法不正确的是( )A、直线与两坐标轴围成的三角形面积是2 B、若三条直线 , , 能构成三角形,则的取值范围是且 C、任意一条过点的直线方程可表示为 D、经过点且在轴和轴上截距都相等的直线方程为12. 已知两圆为与 , 则( )A、若两圆外切,则 B、若两圆有3条公切线,则 C、若两圆公共弦所在直线方程为 , 则 D、为圆上任一点,为圆上任一点,若的最大值为 , 则13. 若椭圆的焦点为 , (),长轴长为 , 则椭圆上的点满足( )A、 B、 C、 D、
A、 B、 C、 共线 D、 与正方体表面积的数值相等11. 下列说法不正确的是( )A、直线与两坐标轴围成的三角形面积是2 B、若三条直线 , , 能构成三角形,则的取值范围是且 C、任意一条过点的直线方程可表示为 D、经过点且在轴和轴上截距都相等的直线方程为12. 已知两圆为与 , 则( )A、若两圆外切,则 B、若两圆有3条公切线,则 C、若两圆公共弦所在直线方程为 , 则 D、为圆上任一点,为圆上任一点,若的最大值为 , 则13. 若椭圆的焦点为 , (),长轴长为 , 则椭圆上的点满足( )A、 B、 C、 D、三、填空题
-
14. 若 , 则 .15. 直线 , 直线 , 则之间的距离是 .16. 已知双曲线的一条渐近线方程为 , 则 .17. 平面直角坐标系中,已知点 , , , , 当四边形的周长最小时,的外接圆的方程为 .
四、解答题
-
18. “十三五”期间,依靠不断增强的综合国力和自主创新能力,我国桥梁设计建设水平不断提升,创造了多项世界第一,为经济社会发展发挥了重要作用,下图是我国的一座抛物线拱形拉索大桥,该桥抛物线拱形部分的桥面跨度为64米,拱形最高点与桥面的距离为32米.
 (1)、求该桥抛物线拱形部分对应抛物线的焦准距(焦点到准线的距离).(2)、已知直线是抛物线的对称轴,为直线与水面的交点,为抛物线上一点,分别为抛物线的顶点和焦点.若 , , 求桥面与水面的距离.19. 已知椭圆的焦距为6,椭圆上一点与两焦点构成的三角形周长为16.(1)、求椭圆的标准方程;(2)、若直线与交于 , 两点,且线段的中点坐标为 , 求直线的方程.
(1)、求该桥抛物线拱形部分对应抛物线的焦准距(焦点到准线的距离).(2)、已知直线是抛物线的对称轴,为直线与水面的交点,为抛物线上一点,分别为抛物线的顶点和焦点.若 , , 求桥面与水面的距离.19. 已知椭圆的焦距为6,椭圆上一点与两焦点构成的三角形周长为16.(1)、求椭圆的标准方程;(2)、若直线与交于 , 两点,且线段的中点坐标为 , 求直线的方程.
