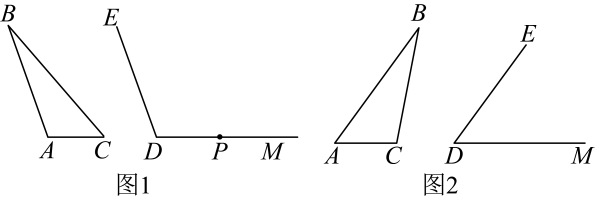【每日15min】10 HL—浙教版数学八(上)微专题复习
试卷更新日期:2023-10-18 类型:复习试卷
一、选择题
-
1. 如图,已知 , 添加下列条件后不能使的是( )
 A、 B、 C、 D、2. 如图,在四边形中, , 平分 , , , , 分别是 , 上的动点,当取得最小值时,的长是( )
A、 B、 C、 D、2. 如图,在四边形中, , 平分 , , , , 分别是 , 上的动点,当取得最小值时,的长是( ) A、8 B、10 C、12 D、163. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,BE平分∠ABC,CD⊥AB于D,BE与CD相交于F,则CF的长是( )
A、8 B、10 C、12 D、163. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,BE平分∠ABC,CD⊥AB于D,BE与CD相交于F,则CF的长是( )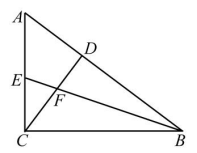 A、1 B、2 C、 D、4. 如图,△ABD和△CBD,∠ADB=90°,∠ABD=∠DBC,AD=DC=1,若AB=4,则BC的长为( )
A、1 B、2 C、 D、4. 如图,△ABD和△CBD,∠ADB=90°,∠ABD=∠DBC,AD=DC=1,若AB=4,则BC的长为( ) A、 B、2 C、3 D、5. 如图,在Rt△ABC中, , , 在AC上取一点E,使 , 过点E作 , 连接CF,使 , 若 , 则AE的长为( )
A、 B、2 C、3 D、5. 如图,在Rt△ABC中, , , 在AC上取一点E,使 , 过点E作 , 连接CF,使 , 若 , 则AE的长为( ) A、5cm B、6cm C、7cm D、无法计算6. 如图,在中于点 , 为上一点连结交于点 , 若 , , 则与的和为( )
A、5cm B、6cm C、7cm D、无法计算6. 如图,在中于点 , 为上一点连结交于点 , 若 , , 则与的和为( ) A、 B、 C、 D、7. 如图,在中, , , 垂足为 , 平分 , 交于点 , 交于点若 , , 则的长为( )
A、 B、 C、 D、7. 如图,在中, , , 垂足为 , 平分 , 交于点 , 交于点若 , , 则的长为( )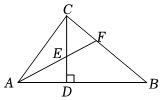 A、4 B、 C、 D、58. 如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E点,DF⊥AC于点F,则下列四个结论:①AD上任意一点到AB,AC两边的距离相等; ②AD⊥BC且BD=CD;③∠BDE=∠CDF;④AE=AF.其中正确的有( )
A、4 B、 C、 D、58. 如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E点,DF⊥AC于点F,则下列四个结论:①AD上任意一点到AB,AC两边的距离相等; ②AD⊥BC且BD=CD;③∠BDE=∠CDF;④AE=AF.其中正确的有( ) A、②③ B、①③ C、①②④ D、①②③④
A、②③ B、①③ C、①②④ D、①②③④二、填空题
-
9. 如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度与右边滑梯的水平长度相等,那么判定与全等的依据是 .
 10. △ABC的角平分线BD与角平分线CE交于点F,连接AF,若∠FBC=25°,FE=FD,则∠FAD为 度.11. 如图,中, , 平分交于点 , 交的延长线于点 , 交于点 . 若 , , . 则的长为 .
10. △ABC的角平分线BD与角平分线CE交于点F,连接AF,若∠FBC=25°,FE=FD,则∠FAD为 度.11. 如图,中, , 平分交于点 , 交的延长线于点 , 交于点 . 若 , , . 则的长为 . 12. 如图,在△ABC中,D为AB中点,DE⊥AB,∠ACE+∠BCE=180°,EF⊥BC交AC于点F,AC=8,BC=12,则BF的长为.
12. 如图,在△ABC中,D为AB中点,DE⊥AB,∠ACE+∠BCE=180°,EF⊥BC交AC于点F,AC=8,BC=12,则BF的长为.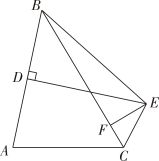
三、解答题
-
13. 如图,已知平分 , 于点E,于点F,且 . 求证: .
 14. 如图,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BD=CD.
14. 如图,已知BE⊥AC于E,CF⊥AB于F,BE、CF相交于点D,若BD=CD.求证:AD平分∠BAC.