【每日15min】9 AAS—浙教版数学八(上)微专题复习
试卷更新日期:2023-10-18 类型:复习试卷
一、选择题
-
1. 如图,和是的高,交于点 , 且 , , 则的长为( )
 A、3 B、4 C、5 D、62. 如图,在和中, , 是的中点, , 垂足为点 , 且 . 若 , 则的长为( )
A、3 B、4 C、5 D、62. 如图,在和中, , 是的中点, , 垂足为点 , 且 . 若 , 则的长为( ) A、2cm B、 C、 D、3. 如图,是上一点,交于点 , , , , , 则的长度为( )
A、2cm B、 C、 D、3. 如图,是上一点,交于点 , , , , , 则的长度为( ) A、2 B、2.5 C、4 D、54. 如图, , , , 则不正确的结论是( )
A、2 B、2.5 C、4 D、54. 如图, , , , 则不正确的结论是( ) A、与互为余角 B、 C、≌ D、5. 如图,A在上,F在上,且 , , 则的长等于( )
A、与互为余角 B、 C、≌ D、5. 如图,A在上,F在上,且 , , 则的长等于( ) A、 B、 C、 D、6. 如图,过边长为的等边三角形的边上一点 , 作于点为延长线上一点,当时,交于 , 则的长为( )
A、 B、 C、 D、6. 如图,过边长为的等边三角形的边上一点 , 作于点为延长线上一点,当时,交于 , 则的长为( ) A、 B、 C、 D、不能确定7. 如图,已知 , , 过点A,且 , , 垂足分别为点 , , 则的长为( )
A、 B、 C、 D、不能确定7. 如图,已知 , , 过点A,且 , , 垂足分别为点 , , 则的长为( ) A、8 B、6 C、4 D、求不出来8. 如图,点P为定角平分线上的一个定点,且与互补.若在绕点P旋转的过程中,其两边分别与、相交于M、N两点,则以下结论中,不正确的是( )
A、8 B、6 C、4 D、求不出来8. 如图,点P为定角平分线上的一个定点,且与互补.若在绕点P旋转的过程中,其两边分别与、相交于M、N两点,则以下结论中,不正确的是( )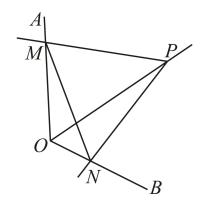 A、的值不变 B、 C、的长不变 D、四边形的面积不变
A、的值不变 B、 C、的长不变 D、四边形的面积不变二、填空题
-
9. 如图,在△ABC中,AD是BC边上的高,BE是AC边上的高,且AD、BE的交于点F,若BF=AC,CD=6,BD=8,则线段AF的长度为 .
 10. 已知:四边形ABCD中,AB=AD=CD,∠BAD=90°,三角形ABC的面积为1,则线段AC的长度是.
10. 已知:四边形ABCD中,AB=AD=CD,∠BAD=90°,三角形ABC的面积为1,则线段AC的长度是. 11. 如图, , 且 , 连接 , 于点 , 于点 . 若 , , , 则的长为 .
11. 如图, , 且 , 连接 , 于点 , 于点 . 若 , , , 则的长为 . 12. 如图,中, , , D为延长线上一点, , 且 , 与的延长线交于点P,若 , 则 .
12. 如图,中, , , D为延长线上一点, , 且 , 与的延长线交于点P,若 , 则 .
三、解答题
-
13. 如图,已知在中, , , 是过点A的一条直线,于点D , 于点E .
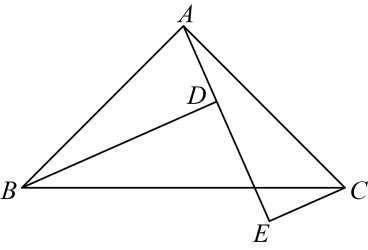 (1)、求证:;(2)、若 , , 求DE的长.14. 学习《利用三角形全等测距离》后,“开拓”小组同学就“测量河两岸、两点间距离”这一问题,设计了如下方案:如图,在点所在河岸同侧平地上取点和点 . 使点、、在一条直线上,且 , 测得 , , 在的延长线上取一点 , 使 , 这时测得的长就是、两点间的距离.你同意他们的说法吗?请说明理由.
(1)、求证:;(2)、若 , , 求DE的长.14. 学习《利用三角形全等测距离》后,“开拓”小组同学就“测量河两岸、两点间距离”这一问题,设计了如下方案:如图,在点所在河岸同侧平地上取点和点 . 使点、、在一条直线上,且 , 测得 , , 在的延长线上取一点 , 使 , 这时测得的长就是、两点间的距离.你同意他们的说法吗?请说明理由. 15. 如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E,F分别是直线CD上两点,且∠BEC=∠CFA=α.
15. 如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E,F分别是直线CD上两点,且∠BEC=∠CFA=α.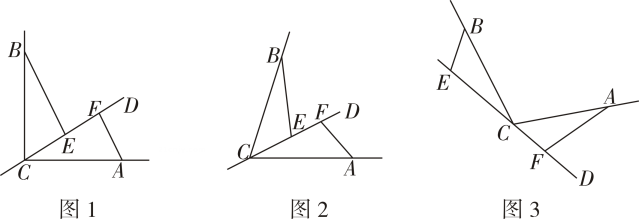 (1)、若直线CD经过∠BCA的内部,且E,F在射线CD上.
(1)、若直线CD经过∠BCA的内部,且E,F在射线CD上.①如图1,若∠BCA=90°,α=90°,证明BE=CF
②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件,使①中的结论仍然成立,并说明理由.
(2)、如图3,若直线CD经过∠BCA的外部,α=∠BCA,请提出关于EF、BE,AF三条线段数量关系的合理猜想,并简述理由.四、实践探究题
-
16. 【问题背景】
如图,在中, , 和的平分线和相交于点G .
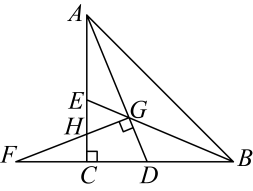
【问题探究】
(1)、的度数为;(2)、过G作交的延长线于点F , 交于点H , 判断与的数量关系,并说明理由;(3)、在(2)的条件下,若 , 求的长.