【每日15min】8 ASA—浙教版数学八（上）微专题复习

试卷更新日期：2023-10-18 类型：复习试卷

进入出卷网下载

一、选择题

1. 一块三角形形状的玻璃破成如图所示的四块，如果用部分碎片配一块与原来形状相同的玻璃，可以使用的碎片编号为（）

A、1，3 B、3，4 C、1，3，4 D、2

查看试题解析
2. 如图，在△DEC和△BFA中，点A，E，F，C在同一直线上，已知AB∥CD，且AB＝CD，若利用“ASA”证明△DEC≌△BFA，则需添加的条件是（）

A、EC＝FA B、∠A＝∠C C、∠D＝∠B D、BF＝DE

查看试题解析
3. 如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=5，BC=3，则BD的长为（）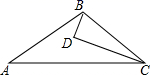

A、1 B、 $1.5$ C、 $2 \sqrt{2}$ D、4

查看试题解析
4. 如图，BP是∠ABC的平分线，AP⊥BP于P，连接PC，若△ABC的面积为16cm² ，则△PBC的面积为（　　）

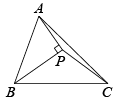A、4cm² B、8cm² C、12cm² D、不能确定

查看试题解析
5. 如图， $A D$ ， $B E$ 是 $△ A B C$ 的高线， $A D$ 与 $B E$ 相交于点 $F$ ．若 $A D = B D$ ，则能判断 $△ A C D ≌ △ B F D$ 的依据是（）

A、 $H L$ B、 $S A S$ C、 $A S A$ D、 $S S S$

查看试题解析
6. 如图所示， $∠ E = ∠ D$ ， $C D ⊥ A C$ 于点 $C$ ， $B E ⊥ A B$ 于点 $B$ ， $A E$ 交 $B C$ 于点 $F$ ，且 $B E = C D$ ，则下列结论不一定正确的是（）

A、 $A B = A C$ B、 $B F = E F$ C、 $A E = A D$ D、 $∠ B A E = ∠ C A D$

查看试题解析
7. 如图，AD，BE是△ABC的高线，AD与BE相交于点F．若AD＝BD＝6，且△ACD的面积为12，则AF的长度为（）

A、4 B、3 C、2 D、1.5

查看试题解析
8. 已知，△ABC，△DEF，△XYZ的相关数据如图所示，则（）

A、 $△ A B C ≌ △ X Y Z$ B、 $△ D E F ≌ △ X Y Z$ C、 $X Y = 12$ D、 $∠ F = 70 °$

查看试题解析

二、填空题

9. 如图，在 $△ A B C$ 和 $△ A D E$ 中， $∠ C A E = ∠ B A D$ ， $A C = A E$ ．

(1)、若添加条件，可用 $S A S$ 推得 $△ A B C$ ≌ $△ A D E$ ；

(2)、若添加条件，可用 $A S A$ 推得 $△ A B C$ ≌ $△ A D E$ ．

查看试题解析
10. 如图，要测量小金河两岸相对的A、 $B$ 两点之间的距离，可以在与 $A B$ 垂直的河岸 $B F$ 上取 $C$ 、 $D$ 两点，且使 $B C = C D$ ．从点 $D$ 出发沿与河岸 $B F$ 垂直的方向移动到点 $E$ ，使点A、 $C$ 、 $E$ 在一条直线上．若测量 $D E$ 的长为28米，则A、 $B$ 两点之间的距离为米．

查看试题解析
11. 如图，在 $△ A B C$ 中， $E$ 为 $A B$ 中点， $D$ 为边 $A C$ 上的动点，连接 $D E$ ， $B F / / A C$ 交 $D E$ 的延长线于点 $F$ ，若 $A C = 5$ ，则 $B F + C D$ 的值是.

查看试题解析
12. 小明沿一段笔直的人行道行走，边走边欣赏风景，在由 $C$ 走到 $D$ 的过程中，通过隔离带的空隙 $P$ ，刚好浏览完对面人行道宣传墙上的一条标语，具体信息如下：如图， $A B / / P M / / C D$ ，相邻两平行线间的距离相等， $A C$ ， $B D$ 相交于 $P$ ， $P D ⊥ C D$ 垂足为 $D .$ 已知 $C D = 165$ 米 $.$ 请根据上述信息求标语 $A B$ 的长度．

查看试题解析
13. 如图，D是 $A B$ 延长线上一点， $D F$ 交 $A C$ 于点E， $A D ∥ F C$ ， $A E = C E$ ．若 $A B = 5$ ， $C F = 8$ ，则 $B D$ 的长是．

查看试题解析
14. 如图，在△ACD中， $∠ C A D = 90 °$ ， AC=6，AD=8， $A B ∥ C D$ ， E是CD上一点，BE交AD于点F，若EF=BF，则图中阴影部分的面积为．

查看试题解析

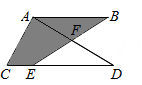
三、解答题

15. 如图，已知，EC=AC，∠BCE=∠DCA，∠A=∠E.

(1)、求证：BC=DC；

(2)、若∠A=25°，∠D=15°，求∠ACB的度数.

查看试题解析
16. 如图，点 $B$ 、 $E$ 、 $C$ 、 $F$ 在同一条直线上， $A C$ 与 $D E$ 相交于点 $O$ ， $A C ∥ D F$ ， $A B ∥ D E$ ， $B E = C F$ ．

(1)、求证： $A C = D F$ ；

(2)、若 $∠ E O C = 80 °$ ， $∠ F = 36 °$ ，求 $∠ B$ 的度数．

查看试题解析

四、实践探究题

17. 阅读与思考
下面是小明同学的数学学习笔记，请您仔细阅读并完成相应的任务：构造全等三角形解决图形与几何问题

在图形与几何的学习中，常常会遇到一些问题无法直接解答，需要添加辅助线才能解决．比如下面的题目中出现了角平分线和垂线段，我们可以通过延长垂线段与三角形的一边相交构造全等三角形，运用全等三角形的性质解决问题．

例：如图1， $D$ 是 $△ A B C$ 内一点，且 $A D$ 平分 $∠ B A C$ ， $C D ⊥ A D$ ，连接 $B D$ ，若 $△ A B D$ 的面积为10，求 $△ A B C$ 的面积．

该问题的解答过程如下：

解：如图2，过点 $B$ 作 $B H ⊥ C D$ 交 $C D$ 延长线于点 $H$ ， $C H$ 、 $A B$ 交于点 $E$ ，

      $∵ A D$ 平分 $∠ B A C$ ，

      $∴ ∠ D A B = ∠ D A C$ ．

      $∵ A D ⊥ C D$ ，

      $∴ ∠ A D C = ∠ A D E = 90 °$ ．

在 $△ A D E$ 和 $△ A D C$ 中， ${\begin{array}{l} ∠ D A E = ∠ D A C \\ A D = A D \\ ∠ A D E = ∠ A D C \end{array}$ ，

      $∴ △ A D E ≌ △ A D C$ （依据1）

$∴ E D = C D$ （依据2）， $S_{△ A D E} = S_{△ A D C}$ ，

      $∵ S_{△ B D E} = \frac{1}{2} D E \cdot B H$ ， $S_{△ B D C} = \frac{1}{2} C D \cdot B H$ ．

……

(1)、任务一：上述解答过程中的依据1，依据2分别是，；

(2)、任务二：请将上述解答过程的剩余部分补充完整；

(3)、应用：如图3，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ， $B E$ 平分 $∠ C B A$ 交 $A C$ 于点 $D$ ，过点 $C$ 作 $C E ⊥ B D$ 交 $B D$ 延长线于点 $E$ ．若 $C E = 6$ ，求 $B D$ 的长．

查看试题解析