重庆市第八名校2023-2024学年高二上册数学开学试卷

试卷更新日期：2023-10-17 类型：开学考试

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共计40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 设 $z = i (2 + i)$ ， $\bar{z}$ 为 $z$ 的共轭复数，则 $\bar{z} =$ （）

A、 $1 + 2 i$ B、 $- 1 - 2 i$ C、 $1 - 2 i$ D、 $- 1 + 2 i$

查看试题解析
2. 已知点P在圆 $x^{2} - 2 \sqrt{3} x + y^{2} - 2 y = 0$ 上，则点P到x轴的距离的最大值为（）

A、2 B、3 C、 $\sqrt{3}$ D、 $\sqrt{3} + 2$

查看试题解析
3. 已知向量 $\vec{a} = (- 2 ， 1)$ ， $\vec{b} = (m ， 2)$ ， $| \vec{a} + \vec{b} | = | \vec{a} - \vec{b} |$ ，则实数m的值为（）．

A、 $- 1$ B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、1

查看试题解析
4. 如图，圆锥 $P O$ 的底面直径和高均是4，过 $P O$ 的中点 $O_{1}$ 作平行于底面的截面，以该截面为底面挖去一个圆柱，则剩下几何体的表面积为（）

A、 $(7 + 4 \sqrt{5}) π$ B、 $(8 + 4 \sqrt{5}) π$ C、 $(9 + 4 \sqrt{5}) π$ D、 $(6 + 4 \sqrt{5}) π$

查看试题解析
5. 在三棱锥A－BCD中，已知 $A B ⊥$ 平面BCD， $B C ⊥ C D$ ，若AB＝2，BC＝CD＝4，则AC与BD所成角的余弦值为（）

A、 $\frac{\sqrt{15}}{5}$ B、 $\frac{2 \sqrt{2}}{3}$ C、 $\frac{\sqrt{10}}{5}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
6. 如图所示， $△ A B C$ 中，点 $D$ 是线段 $B C$ 的中点， $E$ 是线段 $A D$ 上的动点，则 $\vec{B E} = x \vec{B A} + y \vec{B C}$ ，则 $\frac{x + 2 y}{x y}$ 的最小值（）

A、1 B、3 C、5 D、8

查看试题解析
7. 武灵丛台位于邯郸市丛台公园中心处，为园内的主体建筑，是邯郸古城的象征.某校数学兴趣小组为了测量其高度 $A B$ ，在地面上共线的三点 $C$ ， $D$ ， $E$ 处分别测得点 $A$ 的仰角为 $30 °$ ， $45 °$ ， $60 °$ ，且 $C D = D E = 22 m$ ，则武灵丛台的高度 $A B$ 约为（）
（参考数据： $\sqrt{6} \approx 2.449$ ）

A、22m B、27m C、30m D、33m

查看试题解析
8. 在 $△ A B C$ 中， $A = \frac{π}{6}$ ， $B = \frac{π}{2}$ ， $B C = 1$ ， $D$ 为 $A C$ 中点，若将 $△ B C D$ 沿着直线 $B D$ 翻折至 $△ B C^{'} D$ ，使得四面体 $C^{'} - A B D$ 的外接球半径为 $1$ ，则直线 $B C^{'}$ 与平面 $A B D$ 所成角的正弦值是（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{2}{3}$ C、 $\frac{\sqrt{5}}{3}$ D、 $\frac{\sqrt{6}}{3}$

查看试题解析

二、多选题：本题共4小题，每小题5分，共计20分.每小题给出的四个选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得2分.

9. 设 $a$ ， $b$ 是空间中不同的直线， $α$ ， $β$ ， $γ$ 是不同的平面，则下列说法正确的有（）

A、若 $a / / b$ ， $b \subset α$ ， $a ⊄ α$ ，则 $a / / α$ B、若 $a \subset α$ ， $b \subset β$ ， $α / / β$ ，则 $a / / b$ C、若 $a \subset α$ ， $b \subset α$ ， $a / / β$ ， $b / / β$ ，则 $α / / β$ D、若 $α / / β$ ， $α \cap γ = a$ ， $β ∩ γ = b$ ，则 $a / / b$

查看试题解析
10. 下列结论正确的是（）

A、两个不同的平面 $α ， β$ 的法向量分别是 $\vec{u} = (2 ， 2 ， - 1) ， \vec{v} = (- 3 ， 4 ， 2)$ ，则 $α ⊥ β$ B、直线 $l$ 的方向向量 $\vec{a} = (0 ， 3 ， 0)$ ，平面 $α$ 的法向量 $\vec{u} = (1 ， 0 ， 2)$ ，则 $l / / α$ C、若 $\vec{A B} = (2 ， - 1 ， - 4) ， \vec{A C} = (4 ， 2 ， 0) ， \vec{A P} = (0 ， - 4 ， - 8)$ ，则点 $P$ 在平面 $A B C$ 内 D、若 $\vec{a} + \vec{b} ， \vec{b} + \vec{c} ， \vec{c} + \vec{a}$ 是空间的一组基底，则向量 $\vec{a} ， \vec{b} ， \vec{c}$ 也是空间一组基底

查看试题解析
11. 已知直线 $l_{1}$ ： $k x + y - 2 k + 3 = 0$ ， $l_{2}$ ： $x - k y + 3 k - 4 = 0$ ，设两直线分别过定点 $A$ ， $B$ ，直线 $l_{1}$ 和直线 $l_{2}$ 的交点为 $P$ ，则下列结论正确的有（）

A、直线 $l_{1}$ 过定点 $A (2 ， - 3)$ ，直线 $l_{2}$ 过定点 $B (4 ， 3)$ B、 $\vec{P A} \cdot \vec{P B} = 0$ C、 $△ P A B$ 面积的最大值为5 D、若 $O (0 ， 0)$ ， $C (- \frac{1}{3} ， 0)$ ，则点 $P$ 恒满足 $\sqrt{10} | P O | = 3 | P C |$

查看试题解析
12. 半正多面体亦称“阿基米德体多面体”，是由边数不全相同的正多边形为面的多面体.某半正多面体由4个正三角形和4个正六边形构成，其可由正四面体切割而成.在如图所示的半正多面体中，若其棱长为1，则下列结论正确的是（）

A、该半正多面体的表面积为 $\frac{21 \sqrt{3}}{4}$ B、该半正多面体的体积为 $\frac{23 \sqrt{2}}{12}$ C、该半正多面体外接球的的表面积为 $\frac{11 π}{2}$ D、若点 $M ， N$ 分别在线段 $D E ， B C$ 上，则 $F M + M N + A N$ 的最小值为 $\sqrt{19}$

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分.

13. 如图所示是利用斜二测画法画出的水平放置的 $△ A B C$ 的直观图，已知 $A^{'} C^{'} ∥ y^{'}$ 轴， $B^{'} C^{'} ∥ x^{'}$ 轴且 $2 A^{'} C^{'} = B^{'} C^{'} = 2$ ，则 $△ A B C$ 的周长为.

查看试题解析
14. 直线 $x s i n α - \sqrt{3} y + 1 = 0$ 的倾斜角的取值范围是.

查看试题解析
15. 已知三角形 $△ A B C$ 中，内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，且 $\vec{A C} \cdot \vec{A B} = b^{2} - \frac{1}{2} a b ， c = 2$ ，则 $a + b$ 的取值范围是.

查看试题解析
16. 德国机械学家莱洛设计的菜洛三角形在工业领域应用广泛．如图，分别以等边三角形 $A B C$ 的顶点为圆心，以边长为半径作圆弧，由这三段圆弧组成的曲边三角形即为莱洛三角形．若该等边三角形 $A B C$ 的边长为 $1$ ， $P$ 为弧 $A B$ 上的一个动点，则 $\vec{P A} \cdot (\vec{P B} + \vec{P C})$ 的最小值为．

查看试题解析

四、解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.

17. 已知 $△ A B C$ 的三个顶点为 $A (4 ， 0)$ ， $B (8 ， 7)$ ， $C (4 ， 6)$ .

(1)、求过点A且平行于 $B C$ 的直线方程；

(2)、求过点B且与A、C距离相等的直线方程.

查看试题解析
18. 已知三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，侧棱垂直于底面，点 $D$ 是 $A B$ 的中点.

(1)、求证： $B C_{1} / /$ 平面 $C A_{1} D$ ；

(2)、若底面 $A B C$ 为边长为2的正三角形， $B B_{1} = \sqrt{3}$ ，求三棱锥 $B_{1} - A_{1} D C$ 的体积.

查看试题解析
19. 如图，已知 $△ A B C$ 的外接圆 $O$ 的半径为4， $\vec{A O} = 2 \vec{A C} + \vec{A B}$ .

(1)、求 $△ A B C$ 中 $A C$ 边的长：

(2)、求 $\vec{O A} \cdot \vec{O B}$ .

查看试题解析
20. 如图，AB是圆O的直径，C是圆O上异于A，B的一点，DC垂直于圆O所在的平面，DC∥EB，DC＝2EB＝2，AB＝4．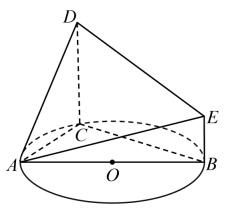

(1)、求证：平面ACD⊥平面EBCD；

(2)、若∠ABC＝30°，求平面ADE与平面ABE所成的锐二面角的余弦值．

查看试题解析
21. 在 $△ A B C$ 中，角 $A ， B ， C$ 所对的边分别为 $a ， b ， c$ ，且 $a + b = 2 c c o s B$ .

(1)、求证： $C = 2 B$ ；

(2)、求 $\frac{a + 3 b}{b c o s B}$ 的最小值.

查看试题解析
22. 如图，在四棱锥 $M - A B C D$ 中， $A D ∥ B C$ ， $A C ⊥ C D$ ， $B C = 2 A D$ ， △MAD为等边三角形，平面 $M A D ⊥$ 平面ABCD，点N在棱MD上，直线 $M B / /$ 平面ACN．

(1)、证明： $M N = 2 N D$ ．

(2)、设二面角 $M - A C - D$ 的平面角为 $α$ ，直线CN与平面ABCD所成的角为 $θ$ ，若 $t a n α$ 的取值范围是 $[3 ， 3 \sqrt{3}]$ ，求 $t a n θ$ 的取值范围．

查看试题解析