山西省大同市浑源县多校2023-2024学年九年级上学期数学月考考试试卷
试卷更新日期:2023-10-16 类型:月考试卷
一、单选题
-
1. 一元二次方程的解为( )A、 B、 , C、 D、 ,2. 如图,一个正方体的边长为 , 它的表面积为 , 则y与x的函数关系式为( )
 A、 B、 C、 D、3. 将一元二次方程化为一般形式后,它的各项系数的和为( )A、6 B、4 C、2 D、4. 二次函数的对称轴为直线( )A、 B、 C、 D、5. 我们解一元二次方程时,可以运用因式分解法将此方程化为 . 从而得到两个一元一次方程:或 , 进而得到原方程的解为 , . 这种解法体现的数学思想是( )A、函数思想 B、数形结合思想 C、转化思想 D、公理化思想6. 一元二次方程根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断其根的情况7. 将抛物线向右平移3个单位长度,再向下平移1个单位长度,得到的抛物线的解析式为( )A、 B、 C、 D、8. 如图,二次函数的图象在平面直角坐标系中的位置大致是( )A、
A、 B、 C、 D、3. 将一元二次方程化为一般形式后,它的各项系数的和为( )A、6 B、4 C、2 D、4. 二次函数的对称轴为直线( )A、 B、 C、 D、5. 我们解一元二次方程时,可以运用因式分解法将此方程化为 . 从而得到两个一元一次方程:或 , 进而得到原方程的解为 , . 这种解法体现的数学思想是( )A、函数思想 B、数形结合思想 C、转化思想 D、公理化思想6. 一元二次方程根的情况为( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断其根的情况7. 将抛物线向右平移3个单位长度,再向下平移1个单位长度,得到的抛物线的解析式为( )A、 B、 C、 D、8. 如图,二次函数的图象在平面直角坐标系中的位置大致是( )A、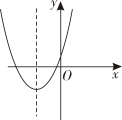 B、
B、 C、
C、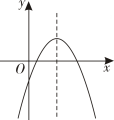 D、
D、 9. 已知m , n是关于x的方程的两个根,则的值为( )A、 B、2 C、 D、410. 已知某二次函数图象上的部分点的横坐标x , 纵坐标y的对应值如下表:
9. 已知m , n是关于x的方程的两个根,则的值为( )A、 B、2 C、 D、410. 已知某二次函数图象上的部分点的横坐标x , 纵坐标y的对应值如下表:x
-3
0
2
y
-6
6
4
下面有四个结论:
①该二次函数的图象经过点;
②当时,该二次的数有最大值为;
③若和都在该二次函数的图象上,则;
④将该二次函数图象向左平移个单位长度后得到函数图象的顶点在y轴上.
其中正确的结论有( )
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 二次函数的图象与轴的交点坐标为 .12. 一元二次方程的较小根为 .13. 如图,已知抛物线经过点 , 且轴, , 则线段的长为 .
 14. 某校为改善校园环境,加大对绿化的投入,2021年对绿化投入资金10万元,2023年对绿化投入资金万元.现假定每年投入绿化资金的增长率相同,则该校投入绿化资金的年平均增长率为 .15. 若关于的方程有三个解,则实数的值是 .
14. 某校为改善校园环境,加大对绿化的投入,2021年对绿化投入资金10万元,2023年对绿化投入资金万元.现假定每年投入绿化资金的增长率相同,则该校投入绿化资金的年平均增长率为 .15. 若关于的方程有三个解,则实数的值是 .三、解答题
-
16.(1)、解方程: .(2)、已知抛物线的顶点是 , 且经过点 , 求该抛物线的函数表达式.17. 关于x的一元二次方程有实数根,求m的取值范围.18. 如图,这是一位篮球运动员投篮的进球路线,球沿抛物线运动,然后准确落人篮筐内.已知投篮运动员在投篮处A到地面的距离米.以O为坐标原点,建立直角坐标系,篮筐的中心D的坐标为 , 对称轴与抛物线交于点B , 与x轴交于点C .
 (1)、求抛物线的表达式.(2)、求点B到所在直线的距离及点B到地面的距离 .19. 太原市某商场进价为100元的某品牌衣服,在销售期间发现,当销售单价定价为200元时,每天可卖出100件.临近2023年十一国庆,商家决定开启大促销活动,经过调研发现:当销售单价下降1元时,每天销售量增加4件.设该品牌衣服每件降价x元.(1)、求每天的销售量y(件)关于x(元)的函数关系式.(2)、在销售单价不低于150元的前提下,计算出该品牌衣服的销售单价定为多少元时,商场每天获利13600元.20. 如图,已知抛物线经过点 , , , 是抛物线对称轴上的一点,且点在第一象限.
(1)、求抛物线的表达式.(2)、求点B到所在直线的距离及点B到地面的距离 .19. 太原市某商场进价为100元的某品牌衣服,在销售期间发现,当销售单价定价为200元时,每天可卖出100件.临近2023年十一国庆,商家决定开启大促销活动,经过调研发现:当销售单价下降1元时,每天销售量增加4件.设该品牌衣服每件降价x元.(1)、求每天的销售量y(件)关于x(元)的函数关系式.(2)、在销售单价不低于150元的前提下,计算出该品牌衣服的销售单价定为多少元时,商场每天获利13600元.20. 如图,已知抛物线经过点 , , , 是抛物线对称轴上的一点,且点在第一象限.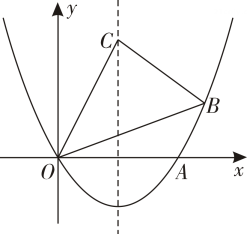 (1)、求抛物线的函数解析式.(2)、当时,求点的坐标.21. 阅读与思考
(1)、求抛物线的函数解析式.(2)、当时,求点的坐标.21. 阅读与思考请阅读下列材料,完成后面的任务:
一元二次方程根的两个性质及其应用
我们知道,一元二次方程的求根公式是 , 由公式可知,一元二次方程的根是由它的系数决定的,即它的根与系数有着密切的关系,那么一元二次方程的根与系数有何关系?下面介绍一元二次方程的两个根与系数关系的另外两个性质(非根与系数的关系定理,即非韦达定理):
性质1:在一元二次方程中,若(即各项的系数和为0),则一元二次方程的两个根分别是 , . 下面我们给出它的证明过程:
证明:∵ , ∴ ,
∴ ,
∴ , .
性质2:在一元二次方程中,若 , 则一元二次方程的两个根分别是 , .
证明:…….
任务:
(1)、填空:下列方程的根是的是 , 根是的是 . (填序号). ; . ; . ; . .
(2)、请参考小论文中性质1的证明过程,写出性质2的证明过程.22. 综合与实践【项目学习】
配方法是数学中重要的一种思想方法,利用配方法可求一元二次方程的根,也可以求二次函数的顶点坐标等.所谓配方法是指将一个式子的某部分通过恒等变形化为完全平方式或几个完全平方式的和的方法.其实这种方法还经常被用到代数式的变形中,并结合非负数的意义解决某些问题.
例1:把代数式进行配方.
解:原式 .
例2:求代数式的最大值.
解:原式 .
, ,
, 的最大值为 .
【问题解决】
(1)、若满足 , 求的值.(2)、若等腰的三边长均为整数,且满足 , 求的周长.(3)、如图,这是美国总统加菲尔德证明勾股定理的一个图形,其中是和的三边长,根据勾股定理可得 , 我们把关于的一元二次方程称为“勾系一元二次方程”.已知实数满足等式 , 且的最小值是“勾系一元二次方程”的一个根.四边形的周长为 , 试求的面积.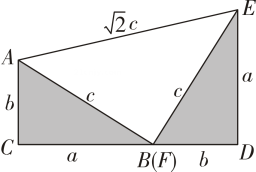 23. 综合与探究
23. 综合与探究如图1,已知抛物线与x轴相交于点 , , 与y轴交于点C .
 (1)、求抛物线及直线的函数解析式.(2)、如图2,P是直线下方的抛物线上的一点,过点P作轴于点Q , 交直线AC于点D , 当时,求点P的坐标.(3)、如图3,过点O作于点M , 将线段OM所在的直线沿着x轴平移,使得平移后的直线交x轴于点E , 交抛物线于点F , 是否存在点F , 使得四边形是平行四边形?若存在,直接写出点F的坐标;若不存在,请说明理由.
(1)、求抛物线及直线的函数解析式.(2)、如图2,P是直线下方的抛物线上的一点,过点P作轴于点Q , 交直线AC于点D , 当时,求点P的坐标.(3)、如图3,过点O作于点M , 将线段OM所在的直线沿着x轴平移,使得平移后的直线交x轴于点E , 交抛物线于点F , 是否存在点F , 使得四边形是平行四边形?若存在,直接写出点F的坐标;若不存在,请说明理由.