河北省石家庄市正定县2022-2023学年七年级下学期期末数学试卷
试卷更新日期:2023-10-16 类型:期末考试
一、选择题(本大题共16小题,共32.0分。在每小题列出的选项中,选出符合题目的一项)
-
1.
如图,经过直线a外一点O的4条直线中,与直线a相交的直线至少有( )
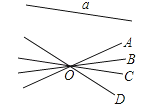 A、4条 B、3条 C、2条 D、1条2. 下列是二元一次方程的是( )A、 B、 C、 D、3. 在等式中,括号内的代数式为( )A、 B、 C、 D、4. 如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( )
A、4条 B、3条 C、2条 D、1条2. 下列是二元一次方程的是( )A、 B、 C、 D、3. 在等式中,括号内的代数式为( )A、 B、 C、 D、4. 如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( )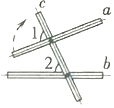 A、10° B、20° C、50° D、70°5. 一次抽奖活动特等奖的中奖率为 ,把 用科学记数法表示为( )A、 B、 C、 D、6. 下列各式从左边到右边的变形是因式分解的是( )A、 B、 C、 D、7. 如果的解集为 , 那么的取值范围是( )A、 B、 C、 D、是任意实数8. 如图,将折叠,使点落在边处,展开后得到折痕 , 则是的( )
A、10° B、20° C、50° D、70°5. 一次抽奖活动特等奖的中奖率为 ,把 用科学记数法表示为( )A、 B、 C、 D、6. 下列各式从左边到右边的变形是因式分解的是( )A、 B、 C、 D、7. 如果的解集为 , 那么的取值范围是( )A、 B、 C、 D、是任意实数8. 如图,将折叠,使点落在边处,展开后得到折痕 , 则是的( ) A、高线 B、角平分线 C、中线 D、中位线9. 已知三角形的三边长分别是3,8,x;若x的值为偶数,则x的值有( )
A、高线 B、角平分线 C、中线 D、中位线9. 已知三角形的三边长分别是3,8,x;若x的值为偶数,则x的值有( )
A、6个; B、5个; C、4个; D、3个.10. 运行程序如图所示,规定:从“输入一个值 ”到“结果是否 ”为一次程序操作,如果程序操作进行了1次后就停止,则 最小整数值取多少( ) A、7 B、8 C、9 D、1011. 如图,已知“”“”“”分别表示三种不同物体,用天平比较它们的质量大小,两次情况如图所示,那么每个“”“”“”的物体按质量从大到小的顺序排列为( )
A、7 B、8 C、9 D、1011. 如图,已知“”“”“”分别表示三种不同物体,用天平比较它们的质量大小,两次情况如图所示,那么每个“”“”“”的物体按质量从大到小的顺序排列为( )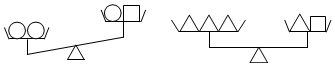 A、 B、 C、 D、12. 如图,是的高,是的角平分线,若 , , 则的度数是( )
A、 B、 C、 D、12. 如图,是的高,是的角平分线,若 , , 则的度数是( ) A、 B、 C、 D、13. 如图,下列条件中,能判定的是( )
A、 B、 C、 D、13. 如图,下列条件中,能判定的是( )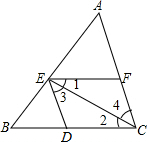 A、 B、 C、 D、14. 某班学生分组搞活动,若每组7人,则余下4人;若每组8人,则有一组少3人.设全班有学生x 人,分成y 个小组,则可得方程组( )A、 B、 C、 D、15. 如图,在中, , 分别是 , 的中点,点在上,且 , 若 , 则( )
A、 B、 C、 D、14. 某班学生分组搞活动,若每组7人,则余下4人;若每组8人,则有一组少3人.设全班有学生x 人,分成y 个小组,则可得方程组( )A、 B、 C、 D、15. 如图,在中, , 分别是 , 的中点,点在上,且 , 若 , 则( ) A、 B、 C、 D、16. 对于关于 , 的二元一次方程组 , 甲、乙两人的判断如下甲:当这个方程组的解 , 的值互为相反数时,;乙:无论取何值,的值始终不变则( )A、甲的判断正确 B、乙的判断正确 C、甲、乙的判断都正确 D、甲、乙的判断都不正确
A、 B、 C、 D、16. 对于关于 , 的二元一次方程组 , 甲、乙两人的判断如下甲:当这个方程组的解 , 的值互为相反数时,;乙:无论取何值,的值始终不变则( )A、甲的判断正确 B、乙的判断正确 C、甲、乙的判断都正确 D、甲、乙的判断都不正确二、填空题(本大题共4小题,共12.0分)
-
17. .18. 已知是完全平方式,把分解因式得: .19. 若关于的不等式组无解,则的取值范围是 .20. ①如图 , 在内部任取一点 , 则图中互不重叠的所有角的和是 ;
②在图中的任一小三角形内任取一点如图 , 则图中互不重叠的所有角的和是 ;
③以此类推,当取到点时,图中互不重叠的所有角的和是 用含的代数式表示 .

三、解答题(本大题共6小题,共56.0分。解答应写出文字说明,证明过程或演算步骤)
-
21. 请你阅读老师的新定义运算规定,然后解答下列各小题.
老师:我们定义一个关于实数 , 的新运算,规定: .
例如: .
(1)、若 , , 分别求出和的值;(2)、若满足 , 且 , 求的取值范围.22. 如图,约定:上方相邻两整式之和等于这两个整式下方箭头共同指向的整式. (1)、求整式 , ;(2)、将整式因式分解.23. 如图,将两个长方形用不同方式拼成图和图两个图形.
(1)、求整式 , ;(2)、将整式因式分解.23. 如图,将两个长方形用不同方式拼成图和图两个图形. (1)、若图中的阴影部分面积为 , 则图中的阴影部分面积为 用含字母 , 的代数式表示;(2)、由你可以得到的等式是 ;(3)、根据你所得到的等式解决下面的问题:
(1)、若图中的阴影部分面积为 , 则图中的阴影部分面积为 用含字母 , 的代数式表示;(2)、由你可以得到的等式是 ;(3)、根据你所得到的等式解决下面的问题:若 , , 则 _▲_ ;
计算: .
解方程: .24. 如图 , , 点 , 分别在射线和上, . (1)、若 , 则 .(2)、嘉嘉同学发现:无论如何变化,的值始终为定值,并给出了一种证明该发现的辅助线作法如图 , 过点作 , 交于点 , 请你根据嘉嘉同学提供的辅助线,先确定该定值再说明理由.(3)、如图 , 把“”改为“”,其他条件保持不变,直接写出与的数量关系.25. 年冬奥会上智慧化全覆盖,机器人得到广泛应用,冬奥会组委会针对不同的物品运送场景选取了几个不同类型的智能物流机器人这样不仅能高效运输,同时也能减少人员接触。具体运输情况如表所示:
(1)、若 , 则 .(2)、嘉嘉同学发现:无论如何变化,的值始终为定值,并给出了一种证明该发现的辅助线作法如图 , 过点作 , 交于点 , 请你根据嘉嘉同学提供的辅助线,先确定该定值再说明理由.(3)、如图 , 把“”改为“”,其他条件保持不变,直接写出与的数量关系.25. 年冬奥会上智慧化全覆盖,机器人得到广泛应用,冬奥会组委会针对不同的物品运送场景选取了几个不同类型的智能物流机器人这样不仅能高效运输,同时也能减少人员接触。具体运输情况如表所示:型机器人个
型机器人个
运输物品总数件
第一批
第二批
问:
(1)、每个型机器人和型机器人分别可以运输物品多少件?(2)、若每个型机器人售价万元,每个型机器人售价万元,该公司计划采购 , 两种型号的机器人共个,总费用不超过万元,那么型号机器人最多购买多少个?26. 如图①,在△ABC 中,∠ABC与∠ACB的平分线相交于点P. (1)、如果∠A=70°,求∠BPC的度数;(2)、如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q,∠A之间的数量关系.(3)、如图③,延长线段BP,QC交于点E,在△BQE中,存在一个内角等于另一个内角的3倍,求∠A的度数.
(1)、如果∠A=70°,求∠BPC的度数;(2)、如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q,∠A之间的数量关系.(3)、如图③,延长线段BP,QC交于点E,在△BQE中,存在一个内角等于另一个内角的3倍,求∠A的度数.