苏科版八年级数学上册《第一章全等三角形》综合检测卷
试卷更新日期:2023-10-16 类型:单元试卷
一、选择题
-
1. 下列说法正确是A、全等三角形是指形状相同的两个三角形 B、全等三角形是指面积相等的两个三角形 C、两个等边三角形是全等三角形 D、全等三角形是指两个能完全重合的三角形2. 如图,≌ , , 是对应点,下列结论错误的是( )
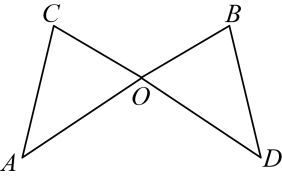 A、和是对应角 B、和是对应角 C、与是对应边 D、和是对应边3. 如图, , , 记 , , 当时,α与β之间的数量关系为( )
A、和是对应角 B、和是对应角 C、与是对应边 D、和是对应边3. 如图, , , 记 , , 当时,α与β之间的数量关系为( ) A、 B、 C、 D、4. 如图,点、在上, , , , , , 则的长为( )
A、 B、 C、 D、4. 如图,点、在上, , , , , , 则的长为( ) A、4 B、 C、3 D、5. 如图,点A , E , F , D在同一直线上,若 , , , 则图中的全等三角形共有( )
A、4 B、 C、3 D、5. 如图,点A , E , F , D在同一直线上,若 , , , 则图中的全等三角形共有( ) A、0对 B、1对 C、2对 D、3对6. 如图,在中,D,E是边上的两点, , 则的度数为( )
A、0对 B、1对 C、2对 D、3对6. 如图,在中,D,E是边上的两点, , 则的度数为( ) A、90° B、80° C、70° D、60°7. 如图是高空秋千的示意图,小明从起始位置点A处绕着点O经过最低点B,最终荡到最高点C处,若 , 点A与点B的高度差AD=1米,水平距离BD=4米,则点C与点B的高度差CE为( )
A、90° B、80° C、70° D、60°7. 如图是高空秋千的示意图,小明从起始位置点A处绕着点O经过最低点B,最终荡到最高点C处,若 , 点A与点B的高度差AD=1米,水平距离BD=4米,则点C与点B的高度差CE为( ) A、4米 B、4.5米 C、5米 D、5.5米8. 如图,在中,为中线,过点B作于点E,过点C作于点F.在延长线上取一点G,连接 , 使 . 下列结论中正确的个数为( )
A、4米 B、4.5米 C、5米 D、5.5米8. 如图,在中,为中线,过点B作于点E,过点C作于点F.在延长线上取一点G,连接 , 使 . 下列结论中正确的个数为( )①;②;③;④
 A、1个 B、2个 C、3个 D、4个9. 如图, 于点 , 于点 , . 要根据证明 , 则还需要添加的条件是( )
A、1个 B、2个 C、3个 D、4个9. 如图, 于点 , 于点 , . 要根据证明 , 则还需要添加的条件是( ) A、 B、 C、 D、10. 如图,在中,平分交于点D , 延长到点E , 使得 , 连接 . 若 , 则的度数是( )
A、 B、 C、 D、10. 如图,在中,平分交于点D , 延长到点E , 使得 , 连接 . 若 , 则的度数是( )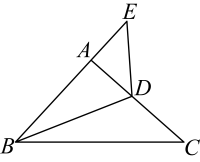 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,、、在同一直线上,≌ , , 那么度.
 12. 如图,点、、、在一条直线上,已知 , , 请你添加一个适当的条件使得≌ .
12. 如图,点、、、在一条直线上,已知 , , 请你添加一个适当的条件使得≌ . 13. 如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为
13. 如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为 14. 如图, , ,且 ,则 .
14. 如图, , ,且 ,则 . 15. 如图,已知 AB//CF,E为DF的中点,若AB=13cm,CF=7cm,则BD=cm .
15. 如图,已知 AB//CF,E为DF的中点,若AB=13cm,CF=7cm,则BD=cm . 16. 如图,等腰中, , 平分 , 于 , 若 , 则的周长是 .
16. 如图,等腰中, , 平分 , 于 , 若 , 则的周长是 . 17. 在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,PR=PS,AQ=PQ,则下面三个结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是.
17. 在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,PR=PS,AQ=PQ,则下面三个结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是.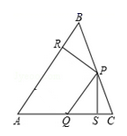 18. 如图,CA⊥AB,垂足为点A,AB=8cm,AC=4cm,射线BM⊥AB,垂足为点B,一动点E从A点出发,以2cm/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E运动秒时,点B、D、E组成的三角形与点A、B、C组成的三角形全等.
18. 如图,CA⊥AB,垂足为点A,AB=8cm,AC=4cm,射线BM⊥AB,垂足为点B,一动点E从A点出发,以2cm/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E运动秒时,点B、D、E组成的三角形与点A、B、C组成的三角形全等.
三、解答题
-
19. 如图,点A、B、C、D在同一直线上,AM=CN , BM=DN , AC=BD . 求证:BM∥DN .
 20. 如图,在中,O为的中点, , 直线交于点E.
20. 如图,在中,O为的中点, , 直线交于点E.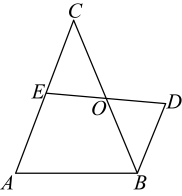 (1)、求证:;(2)、若 , 求的长.21. 如图,点B在CD上,OB=OD , AB=CD , ∠OBA=∠D;
(1)、求证:;(2)、若 , 求的长.21. 如图,点B在CD上,OB=OD , AB=CD , ∠OBA=∠D; (1)、求证:△ABO≌△CDO;(2)、当AO∥CD , ∠BOD=30°,求∠A的度数.22. 如图,在中, , 于点 , , 平分交于点 , 的延长线交于点 . 求证: .
(1)、求证:△ABO≌△CDO;(2)、当AO∥CD , ∠BOD=30°,求∠A的度数.22. 如图,在中, , 于点 , , 平分交于点 , 的延长线交于点 . 求证: . 23. 如图,在中,是延长线上一点,满足 , 过点作 , 且 , 连接并延长,分别交 , 于点 , .(1)、求证:≌;(2)、若 , , 求的长度.
23. 如图,在中,是延长线上一点,满足 , 过点作 , 且 , 连接并延长,分别交 , 于点 , .(1)、求证:≌;(2)、若 , , 求的长度. 24. 已知 , , , , 垂足分别为点D , E .
24. 已知 , , , , 垂足分别为点D , E .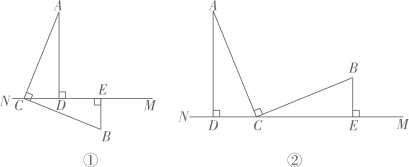 (1)、如图①,求证:(2)、如图②,(1)中的结论还成立吗?如果不成立,请写出线段AD , BE , DE之间的数量关系,并说明理由.25. 将两个全等的直角三角形和直角三角形按图方式摆放,其中 , , 点落在上,所在直线交所在直线于点 .
(1)、如图①,求证:(2)、如图②,(1)中的结论还成立吗?如果不成立,请写出线段AD , BE , DE之间的数量关系,并说明理由.25. 将两个全等的直角三角形和直角三角形按图方式摆放,其中 , , 点落在上,所在直线交所在直线于点 . (1)、求证: .(2)、如图 , 若将图中的绕点按顺时针方向旋转角 , 且 , 其他条件不变,证明: .(3)、若将图中的绕点按顺时针方向旋转角 , 且 , 其他条件不变,如图你认为(2)中的结论还成立吗?若成立,写出证明过程:若不成立,请直接写出此时、与之间的关系.26. 如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E,F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)、求证: .(2)、如图 , 若将图中的绕点按顺时针方向旋转角 , 且 , 其他条件不变,证明: .(3)、若将图中的绕点按顺时针方向旋转角 , 且 , 其他条件不变,如图你认为(2)中的结论还成立吗?若成立,写出证明过程:若不成立,请直接写出此时、与之间的关系.26. 如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E,F分别是直线CD上两点,且∠BEC=∠CFA=α.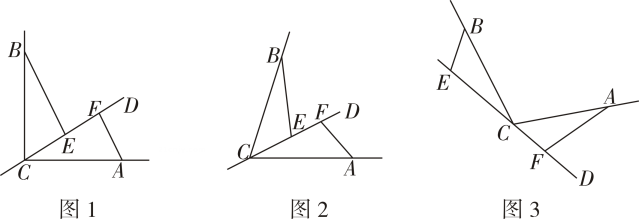 (1)、若直线CD经过∠BCA的内部,且E,F在射线CD上.
(1)、若直线CD经过∠BCA的内部,且E,F在射线CD上.①如图1,若∠BCA=90°,α=90°,证明BE=CF
②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件,使①中的结论仍然成立,并说明理由.
(2)、如图3,若直线CD经过∠BCA的外部,α=∠BCA,请提出关于EF、BE,AF三条线段数量关系的合理猜想,并简述理由.