人教版八年级上册数学《第十二章全等三角形》能力提升卷
试卷更新日期:2023-10-16 类型:单元试卷
一、选择题
-
1. 如图,已知 , , , 则的长为( )
 A、7 B、3.5 C、3 D、22. 如图,点 , , , 在同一条直线上, , , 则添加下列条件中的一个条件后,不一定能判定≌的是( )
A、7 B、3.5 C、3 D、22. 如图,点 , , , 在同一条直线上, , , 则添加下列条件中的一个条件后,不一定能判定≌的是( )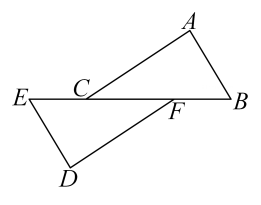 A、 B、 C、 D、3. 在△ABC与△A′B′C′中,已知∠A=∠A′,AC=A′C′,下列说法错误的是( )A、若添加条件AB=A′B′,则△ABC与△A′B′C′全等 B、若添加条件∠C=∠C′,则△ABC与△A′B′C′全等 C、若添加条件∠B=∠B′,则△ABC与△A′B′C′全等 D、若添加条件BC=B′C′,则△ABC与△A′B′C′全等4. 已知,如图,是内部的一条射线,是射线上任意点, , , 下列条件中: , , , , 能判定是的角平分线的有( )
A、 B、 C、 D、3. 在△ABC与△A′B′C′中,已知∠A=∠A′,AC=A′C′,下列说法错误的是( )A、若添加条件AB=A′B′,则△ABC与△A′B′C′全等 B、若添加条件∠C=∠C′,则△ABC与△A′B′C′全等 C、若添加条件∠B=∠B′,则△ABC与△A′B′C′全等 D、若添加条件BC=B′C′,则△ABC与△A′B′C′全等4. 已知,如图,是内部的一条射线,是射线上任意点, , , 下列条件中: , , , , 能判定是的角平分线的有( )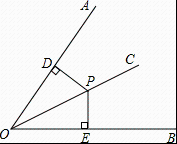 A、个 B、个 C、个 D、个5. 如图,在中, , 的角平分线交于点D,于点E,若与的周长分别为13和3,则的长为( )
A、个 B、个 C、个 D、个5. 如图,在中, , 的角平分线交于点D,于点E,若与的周长分别为13和3,则的长为( ) A、10 B、16 C、8 D、56. 如图, , , 记 , , 当时,α与β之间的数量关系为( )
A、10 B、16 C、8 D、56. 如图, , , 记 , , 当时,α与β之间的数量关系为( ) A、 B、 C、 D、7. 如图,平分 , , , , , 则的长为( )
A、 B、 C、 D、7. 如图,平分 , , , , , 则的长为( ) A、13 B、12 C、11 D、108. 如图,在平面直角坐标系中,的顶点 , , 点在第四象限,且 , , 则点的坐标是( )
A、13 B、12 C、11 D、108. 如图,在平面直角坐标系中,的顶点 , , 点在第四象限,且 , , 则点的坐标是( ) A、 B、 C、 D、9. 如图,中,、的角平分线、交于点 , 延长、 , , 则下列结论中正确的个数( )
A、 B、 C、 D、9. 如图,中,、的角平分线、交于点 , 延长、 , , 则下列结论中正确的个数( )
平分;;; .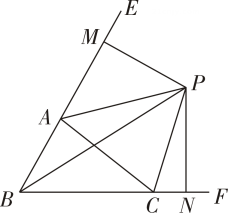 A、个 B、个 C、个 D、个10. 如图,在长方形中, , , 点P从点A出发,以每秒1个单位长度的速度沿向点B匀速运动,点Q从点B出发,以每秒2个单位长度的速度沿向点C匀速运动,点R从点C出发,以每秒a个单位长度的速度沿向点D运动,连接 , . 三点同时开始运动,当某一点运动到终点时,其它点也停止运动,若在某一时刻,与全等,则a的值为( )
A、个 B、个 C、个 D、个10. 如图,在长方形中, , , 点P从点A出发,以每秒1个单位长度的速度沿向点B匀速运动,点Q从点B出发,以每秒2个单位长度的速度沿向点C匀速运动,点R从点C出发,以每秒a个单位长度的速度沿向点D运动,连接 , . 三点同时开始运动,当某一点运动到终点时,其它点也停止运动,若在某一时刻,与全等,则a的值为( ) A、2或4 B、2或 C、2或 D、2或
A、2或4 B、2或 C、2或 D、2或二、填空题
-
11. 如图,点E , F在上, , , 请你添加一个条件(不添加字母和辅助线),使得≌ , 你添加的条件是 .
 12. 如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD=度.
12. 如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD=度. 13. 如图,平分 , 于点 , 点在射线上,且 . 若 , , , 则的长为 .
13. 如图,平分 , 于点 , 点在射线上,且 . 若 , , , 则的长为 .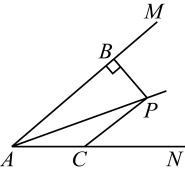 14. 如图,在△ABC中,AD是BC边上的高,BE是AC边上的高,且AD、BE的交于点F,若BF=AC,CD=6,BD=8,则线段AF的长度为 .
14. 如图,在△ABC中,AD是BC边上的高,BE是AC边上的高,且AD、BE的交于点F,若BF=AC,CD=6,BD=8,则线段AF的长度为 . 15. 如图,在中, , 平分 , 垂直平分 , 若的面积等于4,则的面积为.
15. 如图,在中, , 平分 , 垂直平分 , 若的面积等于4,则的面积为. 16. 如图,点 , , , 在同一条直线上, , , 若 , , 则的度数为
16. 如图,点 , , , 在同一条直线上, , , 若 , , 则的度数为 17. 如图,在中,将对折,使和在同一直线上,折痕为 , 延长至点D,使得 , 连接 , 若 , 则 .
17. 如图,在中,将对折,使和在同一直线上,折痕为 , 延长至点D,使得 , 连接 , 若 , 则 . 18. 如图,在△AOB和△COD中,OA=OB , OC=OD(OA<OC),∠AOB=∠COD=α , 直线AC , BD交于点M , 连接OM . 以下结论:①AC=BD;②∠OAM=∠OBM;③∠AMB=α;④OM平分∠BOC . 其中正确的是 . (填序号)
18. 如图,在△AOB和△COD中,OA=OB , OC=OD(OA<OC),∠AOB=∠COD=α , 直线AC , BD交于点M , 连接OM . 以下结论:①AC=BD;②∠OAM=∠OBM;③∠AMB=α;④OM平分∠BOC . 其中正确的是 . (填序号)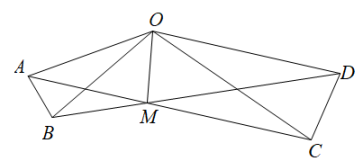
三、解答题
-
19. 如图,点B , E , C , F在一条直线上,AB=DE , AC=DF , BF=CE . 试说明:AB∥DE .
 20. 如图,已知 , , , 与交于点 .
20. 如图,已知 , , , 与交于点 . (1)、求证:≌;(2)、若 , 求的度数.21. 如图,在中,是延长线上一点,满足 , 过点作 , 且 , 连接并延长,分别交 , 于点 , .(1)、求证:≌;(2)、若 , , 求的长度.
(1)、求证:≌;(2)、若 , 求的度数.21. 如图,在中,是延长线上一点,满足 , 过点作 , 且 , 连接并延长,分别交 , 于点 , .(1)、求证:≌;(2)、若 , , 求的长度. 22. 如图,中,CD平分 , 且E为AB的中点,于M,于N,请你判断线段BM与AN的数量关系并加以证明.
22. 如图,中,CD平分 , 且E为AB的中点,于M,于N,请你判断线段BM与AN的数量关系并加以证明. 23. 已知:如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D、E,点F是OC上的另一点,连接DF,EF.求证:DF=EF.
23. 已知:如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D、E,点F是OC上的另一点,连接DF,EF.求证:DF=EF.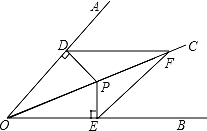 24. 如图,∠B=∠C=90°,M是BC上一点,且DM平分∠ADC,AM平分∠DAB,求证:AD=CD+AB.
24. 如图,∠B=∠C=90°,M是BC上一点,且DM平分∠ADC,AM平分∠DAB,求证:AD=CD+AB.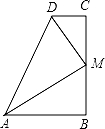 25. 如图,AD是的中线, , 垂足为E, , 交AD的延长线于点F,G是DA延长线上一点,连接BG.
25. 如图,AD是的中线, , 垂足为E, , 交AD的延长线于点F,G是DA延长线上一点,连接BG. (1)、求证:;(2)、若 , 求证: .26. 如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E,F分别是直线CD上两点,且∠BEC=∠CFA=α.
(1)、求证:;(2)、若 , 求证: .26. 如图,CD是经过∠BCA顶点C的一条直线,CA=CB,E,F分别是直线CD上两点,且∠BEC=∠CFA=α.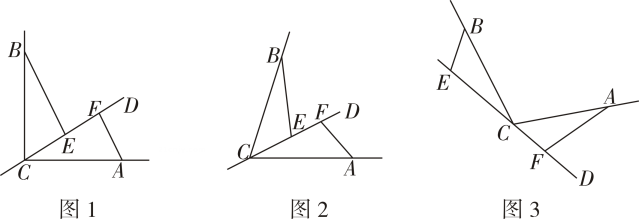 (1)、若直线CD经过∠BCA的内部,且E,F在射线CD上.
(1)、若直线CD经过∠BCA的内部,且E,F在射线CD上.①如图1,若∠BCA=90°,α=90°,证明BE=CF
②如图2,若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件,使①中的结论仍然成立,并说明理由.
(2)、如图3,若直线CD经过∠BCA的外部,α=∠BCA,请提出关于EF、BE,AF三条线段数量关系的合理猜想,并简述理由.