【每日15min】7 SAS—浙教版数学八(上)微专题复习
试卷更新日期:2023-10-15 类型:复习试卷
一、选择题
-
1. 如图,已知BF=DE,AB∥DC,要使△ABF≌△CDE,添加的条件可以是( )
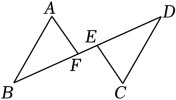 A、BE=DF B、AF=CE C、AB=CD D、∠B=∠D2. 如图,在中,D,E是边上的两点, , 则的度数为( )
A、BE=DF B、AF=CE C、AB=CD D、∠B=∠D2. 如图,在中,D,E是边上的两点, , 则的度数为( ) A、90° B、80° C、70° D、60°3. 如图, , 添加下列条件,能用“”判断 的是( )
A、90° B、80° C、70° D、60°3. 如图, , 添加下列条件,能用“”判断 的是( ) A、 B、 C、 D、4. 在测量一个小口圆形容器的壁厚时,小明用“型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=5厘米,EF=7厘米,圆形容器的壁厚是( )
A、 B、 C、 D、4. 在测量一个小口圆形容器的壁厚时,小明用“型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=5厘米,EF=7厘米,圆形容器的壁厚是( ) A、1厘米 B、2厘米 C、5厘米 D、7厘米5. 如图,是的中线,E,F分别是和延长线上的点,且 , 连接 , , 下列说法:①和面积相等;②;③;④;⑤ . 其中正确的是( )
A、1厘米 B、2厘米 C、5厘米 D、7厘米5. 如图,是的中线,E,F分别是和延长线上的点,且 , 连接 , , 下列说法:①和面积相等;②;③;④;⑤ . 其中正确的是( ) A、①② B、③⑤ C、①③④ D、①④⑤6. 如图,在中, , 则的度数是( )
A、①② B、③⑤ C、①③④ D、①④⑤6. 如图,在中, , 则的度数是( ) A、 B、 C、 D、7. 如图,AD平分∠BAC,AB=AC,连接BD,CD并延长交AC,AB于E,F点,则此图中全等三角形共有( )
A、 B、 C、 D、7. 如图,AD平分∠BAC,AB=AC,连接BD,CD并延长交AC,AB于E,F点,则此图中全等三角形共有( )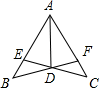 A、2对 B、3对 C、4对 D、5对8. 如图所示 , , , 点 , , 在一条直线上,若 , , 则的长为( )
A、2对 B、3对 C、4对 D、5对8. 如图所示 , , , 点 , , 在一条直线上,若 , , 则的长为( )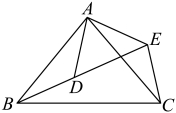 A、2 B、5 C、8 D、15
A、2 B、5 C、8 D、15二、填空题
-
9. 如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为
 10. 如图, , ,且 ,则 .
10. 如图, , ,且 ,则 . 11. 如图,在中, , D,E,F分别是边 , , 上的点,且 , . 若 , 则的度数为°.
11. 如图,在中, , D,E,F分别是边 , , 上的点,且 , . 若 , 则的度数为°. 12. 如图,在中, , 于点D,于点C, . 点E,点F分别在线段上, , 连接 .
12. 如图,在中, , 于点D,于点C, . 点E,点F分别在线段上, , 连接 . (1)、图中与相等的线段是;(2)、当取最小值时°
(1)、图中与相等的线段是;(2)、当取最小值时°三、解答题
-
13. 要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,为卡钳两柄交点(即交于点),且有.如果圆形工件恰好通过卡钳 , 则此工件的外径必是的长.你能说明其中的道理吗?


