【每日15min】1认识三角形—浙教版数学八(上)微专题复习
试卷更新日期:2023-10-15 类型:复习试卷
一、选择题
-
1. 如果一个三角形的两个内角分别为和 , 则这个三角形的形状是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法判断2. 若三角形三个内角度数之比为 , 则这个三角形一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形3. 如果一个三角形的两边长分别为2和4,则第三边长可能是( )A、8 B、6 C、4 D、24. 下列四组数中,以三个数据为长的三条线段能够首尾顺次相接组成三角形的是( )A、1,2,3 B、2,3,3 C、2,3,5 D、2,3,75. 以下四种作边上的高,其中正确的作法是( )A、
 B、
B、 C、
C、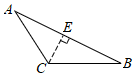 D、
D、 6. 如图,在中,BD是的中线,BE是的中线.若 , 则AC的长度为( )
6. 如图,在中,BD是的中线,BE是的中线.若 , 则AC的长度为( )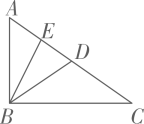 A、3 B、6 C、9 D、127. 已知的底边BC上的高8cm,当它的底边BC从16cm变化到5cm时,的面积( )A、从变化到 B、从变化到 C、从变化到 D、从变化到8. 如图,在中, , , , 分别是的中线、角平分线和高线,交于点 , 交于点 , 下面说法中一定正确的是( )
A、3 B、6 C、9 D、127. 已知的底边BC上的高8cm,当它的底边BC从16cm变化到5cm时,的面积( )A、从变化到 B、从变化到 C、从变化到 D、从变化到8. 如图,在中, , , , 分别是的中线、角平分线和高线,交于点 , 交于点 , 下面说法中一定正确的是( )
的面积等于的面积;
;
;
.
A、 B、 C、 D、二、填空题
-
9. 若一个三角形的三边长分别是 , , , 则x的取值范围是 .10. 如图, , , 点B在射线上,若为钝角三角形,则线段长的取值范围是.
 11. 如图,在中, , , , 平分则的度数为 .
11. 如图,在中, , , , 平分则的度数为 .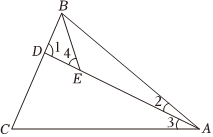 12. 如图,在中,已知点D , E , F分别为边 , , 的中点,且的面积等于 , 则阴影部分图形面积等于 .
12. 如图,在中,已知点D , E , F分别为边 , , 的中点,且的面积等于 , 则阴影部分图形面积等于 .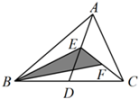
三、解答题
-
13. 如图,在中,是边上的高线,是一条角平分线,它们相交于点P.已知 , , 求的度数.
 14. 如图,在中,是边上的高.
14. 如图,在中,是边上的高. (1)、若是边上的中线, , , 求的长;(2)、若是的平分线, , , 求的大小.15. 如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准直角三角形”.
(1)、若是边上的中线, , , 求的长;(2)、若是的平分线, , , 求的大小.15. 如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准直角三角形”.
 (1)、如图①,在Rt△ABC中,∠ACB=90°,BD是△ABC的角平分线.
(1)、如图①,在Rt△ABC中,∠ACB=90°,BD是△ABC的角平分线.求证:△ABD是“准直角三角形”.
(2)、关于“准直角三角形”,下列说法:①在△ABC中,若∠A=100°,∠B=70°,∠C=10°,则△ABC是准直角三角形;
②若△ABC是“准直角三角形”,∠C>90°,∠A=60°,则∠B=20°;
③“准直角三角形”一定是钝角三角形.其中,正确的是 . (填写序号)
(3)、如图②,B、C为直线l上两点,点A在直线l外,且∠ABC=50°.若P是l上一点,且△ABP是“准直角三角形”,请直接写出∠APB的度数.