【每日15min】11二次函数的实际应用—浙教版数学九（上）微专题复习

试卷更新日期：2023-10-15 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图1所示的矩形窗框ABCD的周长及其两条隔断EF、GH的总长为a米，且隔断EF、GH分别与矩形的两条邻边平行，设BC的长为x米，矩形ABCD的面积为y平方米，y关于x的函数图象如图2，则下列说法正确的是（）

A、矩形ABCD的最大面积为8平方米 B、y与x之间的函数关系式为y＝-x2+2x C、当x＝4时，矩形ABCD的面积最大 D、a的值为12

查看试题解析
2. 学校组织学生去绍兴进行研学实践活动，小王同学发现在宾馆房间的洗手盘台面上有一瓶洗手液（如图①）.于是好奇的小王同学进行了实地测量研究.当小王用一定的力按住顶部A下压如图②位置时，洗手液从喷口B流出，路线近似呈抛物线状，且喷口B为该抛物线的顶点.洗手液瓶子的截面图下面部分是矩形 $C G H D$ .小王同学测得∶洗手液瓶子的底面直径 $G H = 12 c m$ ，喷嘴位置点B距台面的距离为 $16 c m$ ，且 $B 、 D 、 H$ 三点共线.小王在距离台面 $15.5 c m$ 处接洗手液时，手心Q到直线 $D H$ 的水平距离为 $3 c m$ ，若小王不去接，则洗手液落在台面的位置距 $D H$ 的水平面是（） $c m$

A、 $12 \sqrt{3}$ B、 $12 \sqrt{2}$ C、 $6 \sqrt{3}$ D、 $6 \sqrt{2}$

查看试题解析
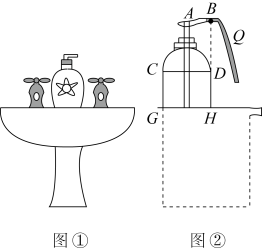3. 用48米木料制作成一个如图所示的“目”形长方形大窗框（横档EF，GH也用木料）．其中AB∥EF∥GH∥CD，要使窗框ABCD的面积最大，则AB的长为（）

A、6米 B、8米 C、12米 D、 $4 \sqrt{3}$ 米

查看试题解析
4. 将进货单价为30元的某种商品按零售价100元1件卖出时，每天能卖出20件．若这种商品的零售价在一定范围内每降价1元，其日销售量就增加1件，为了获得最大的利润，则应降价（）

A、5元 B、15元 C、25元 D、35元

查看试题解析
5. 将进货价格为35元的商品按单价40元售出时，能卖出200个.已知该商品单价每上涨1元，其销售量就减少5个.设这种商品的售价上涨x元时，获得的利润为y元，则下列关系式正确的是（）

A、y＝（x-35）（200-5x） B、y＝（x+40）（200−10x） C、y＝（x+5）（200-5x） D、y＝（x+5）（200−10x）

查看试题解析
6. 某种商品每天的销售利润y（元）与单价x（元）之间的函数关系式为 $y = - 0.1 {(x - 3)}^{2} + 25$ ．则这种商品每天的最大利润为（）

A、0.1元 B、3元 C、25元 D、75元

查看试题解析
7. 如图，小强在某次投篮中，球的运动路线是抛物线 $y = - \frac{1}{5} x^{2} + 3.5$ 的一部分，若命中篮圈中心，则他与篮筐底的距离 $l$ 是（）

A、3m B、3.5m C、4m D、4.5m

查看试题解析
8. 向空中发射一枚炮弹，经x秒后的高度为y米，且时间与高度的关系为y＝ax²+bx+c（a≠0）、若此炮弹在第8秒与第16秒时的高度相等，则在下列时间中炮弹所在高度最高的是（）

A、第8秒 B、第10秒 C、第12秒 D、第15秒

查看试题解析

二、填空题

9. 如图，在矩形 ABCD 中，AD＝3，点E是AD边上的动点，连结CE，以CE为边向右上方作正方形CEFG，过点F作 FH⊥AD，垂足为H，连结AF. 在整个变化过程中，△AEF 面积的最大值是．

查看试题解析
10. 某商场经营一种文具，进价为20元/件，当销售单价是25元时，每天的销售量为250件；销售单价每上涨1元，每天的销售量就减少10件.那么该文具定价为元时每天的最大销售利润最大.

查看试题解析
11. 教练对小明推铅球的录像进行技术分析，建立平面直角坐标系（如图），发现铅球与地面的高度 $y (m)$ 和运动员出手点的水平距离 $x (m)$ 之间的函数关系为 $y = - \frac{1}{10} x^{2} + \frac{4}{5} x + 2$ ，由此可知铅球的落地点与运动员出手点的水平距离是m.

查看试题解析
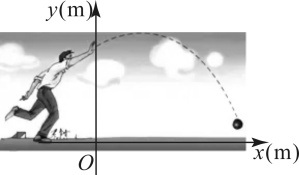12. 某地的药材批发公司指导农民养植和销售某种药材，经市场调研发现1-8月份这种药材售价（元）与月份之间存在如下表所示的一次函数关系，同时，每千克的成本价（元）与月份之间近似满足如图所示的抛物线，观察两幅图表，试判断月份出售这种药材获利最大．
月份
...
3
6
...
每千克售价
...
8
6
...

查看试题解析

三、解答题

13. 如图，在一个边长为 $10 c m$ 的正方形的四个角上，都剪去一个大小相同的小正方形，当小正方形的边长由小到大变化时，图中阴影部分的面积也随之发生变化．

(1)、在这个变化过程中，自变量、因变量各是什么？

(2)、若小正方形的边长为 $x c m (0 < x < 5)$ ，图中阴影部分的面积为 $y c m^{2}$ ，请直接写出y与x之间的关系式；并求出当 $x = 3$ 时，图中阴影部分的面积．

查看试题解析
14. 经营某种品牌的玩具，购进时的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具，设该种品牌玩具的销售单价为x元 $(x ＞ 40)$ ，销售量为y（件），销售该品牌玩具获得利润为w元．

(1)、销售量为y与x关系式为；

(2)、若商场获得了10000元销售利润，求该玩具销售单价x应定为多少元；

(3)、若玩具厂规定该品牌玩具销售单价不低于44元，且商场要完成不少于540件的销售任务，求该商场销售该品牌玩具获得的最大利润是多少？

查看试题解析
15. 嘉嘉和淇淇在玩沙包游戏．某同学借此情境编制了一道数学题，请解答这道题．
如图，在平面直角坐标系中，一个单位长度代表1m长．嘉嘉在点 $A (6 ， 1)$ 处将沙包（看成点）抛出，并运动路线为抛物线 $C_{1} ： y = a (x - 3)^{2} + 2$ 的一部分，淇淇恰在点 $B (0 ， c)$ 处接住，然后跳起将沙包回传，其运动路线为抛物线 $C_{2} ： y = - \frac{1}{8} x^{2} + \frac{n}{8} x + c + 1$ 的一部分．

(1)、写出 $C_{1}$ 的最高点坐标，并求a，c的值；

(2)、若嘉嘉在x轴上方 $1 m$ 的高度上，且到点A水平距离不超过 $1 m$ 的范围内可以接到沙包，求符合条件的n的整数值．

查看试题解析

月份	...	3	6	...
每千克售价	...	8	6	...