【每日15min】10二次函数与一次函数—浙教版数学九（上）微专题复习

试卷更新日期：2023-10-15 类型：复习试卷

进入出卷网下载

一、选择题

1. 在同一平面直角坐标系内，二次函数 $y = x^{2} - m$ 与一次函数 $y = - x + m$ 的图像可能是（）

A、 B、 C、 D、

查看试题解析
2. 如图，函数 $y = a x^{2} + b x + c$ 与 $y = x - 1$ 的图象如图所示，以下结论正确的是（）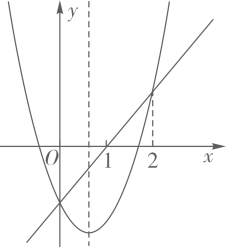

A、 $b c < 0$ B、 $a + b + c > 0$ C、 $2 a + b = 1$ D、当 $0 < x < 2$ 时， $a x^{2} + (b - 1) x + c + 1 > 0$

查看试题解析
3. 抛物线 $y = a x^{2} - a (a \neq 0)$ 与直线 $y = k x$ 交于 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ 两点，若 $x_{1} + x_{2} < 0$ ，则直线 $y = a x + k$ 一定经过（）．

A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限

查看试题解析
4. 已知二次函数 $y = - x^{2} + x + 6$ ，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新的函数图象（如图所示），当直线 $y = - x + m$ 与新图像有3个交点时，m的值是（）

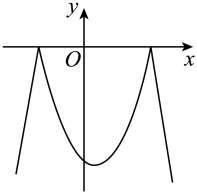A、 $- \frac{25}{4}$ B、-2 C、-2或3 D、-6或-2

查看试题解析
5. 已知抛物线 $y = \frac{1}{4} x^{2}$ 与一次函数 $y = 2 x + 6$ 交于 $A ， B$ 两点，则线段 $A B$ 的长度为（）

A、 $20 \sqrt{2}$ B、 $20 \sqrt{3}$ C、 $40 \sqrt{3}$ D、20

查看试题解析
6. 已知点 $A (x_{1} ， y_{1})$ 在直线 $y = 3 x + 19$ 上，点 $B (x_{2} ， y_{2}) ， C (x_{3} ， y_{3})$ 在抛物线 $y = x^{2} + 4 x - 1$ 上，若 $y_{1} = y_{2} = y_{3}$ 且 $x_{1} < x_{2} < x_{3}$ ，则 $x_{1} + x_{2} + x_{3}$ 的取值范围是（）

A、 $- 12 < x_{1} + x_{2} + x_{3} < - 9$ B、 $- 8 < x_{1} + x_{2} + x_{3} < - 6$ C、 $- 9 < x_{1} + x_{2} + x_{3} < 0$ D、 $- 6 < x_{1} + x_{2} + x_{3} < 1$

查看试题解析
7. 已知二次函数 $y = - x^{2} + x + m^{2} (m > 0)$ 与一次函数 $y = - x + 1$ 交于 $A (x_{1} ， y_{1})$ 、 $B (x_{2} ， y_{2})$ 两点 $(x_{1} < x_{2})$ ，当 $x_{1} \leq x \leq x_{2}$ 时，至少存在一个x使得 $- x^{2} + x + m^{2} \geq \frac{1}{3}$ 成立，则m的取值范围是（）

A、 $0 < m \leq \frac{1}{5}$ B、 $\frac{1}{5} \leq m \leq \frac{1}{4}$ C、 $\frac{1}{4} \leq m \leq \frac{1}{3}$ D、 $m \geq \frac{1}{3}$

查看试题解析
8. 定义：两个不相交的函数图象在平行于 $y$ 轴方向上的最短距离称为这两个函数的“完美距离”．抛物线 $y = 2 x^{2} - 5 x + 3$ 与直线 $y = - 2 x - 1$ 的“完美距离”为（）

A、 $\frac{23}{8}$ B、3 C、 $\frac{27}{8}$ D、 $\frac{21}{8}$

查看试题解析
9. 课堂上，老师给出一道题：如图，将抛物线C：y＝x²-6x+5在x轴下方的图象沿x轴翻折，翻折后得到的图象与抛物线C在x轴上方的图象记为G，已知直线l：y＝x+m与图象G有两个公共点，求m的取值范围甲同学的结果是-5＜m＜-1，乙同学的结果是m＞ $\frac{5}{4}$ ．下列说法正确的是（）

A、甲的结果正确 B、乙的结果正确 C、甲、乙的结果合在一起才正确 D、甲、乙的结果合在一起也错误

查看试题解析

二、填空题

10. 已知直线y＝2x和抛物线y＝ax²+3相交于点（2，b），则a+b＝．

查看试题解析
11. 已知抛物线y₁：y＝2（x﹣3）²+1和抛物线y₂：y＝﹣2x²﹣8x﹣3，若无论k取何值，直线y＝kx+km+n被两条抛物线所截的两条线段都保持相等，则m＝， n＝．

查看试题解析
12. 如图，函数 $y = {\begin{array}{l} - x^{2} + 2 x (x > 0) \\ - x (x < 0) \end{array}$ 的图象，若直线 $y = x + m$ 与该图象只有一个交点，则 $m$ 的取值范围为 .

查看试题解析

三、综合题

13. 已知函数 $y_{1} = (x + m) (x - m - 1)$ ， $y_{2} = a x + m (a \neq 0)$ 在同一平面直角坐标系中.

(1)、若 $y_{1}$ 经过点（1，-2），求 $y_{1}$ 的函数表达式.

(2)、若 $y_{2}$ 经过点（1，m+1），判断 $y_{1}$ 与 $y_{2}$ 图象交点的个数，说明理由.

(3)、若y₁经过点（ $\frac{1}{2}$ ， 0)，且对任意x，都有 $y_{1} > y_{2}$ ，请利用图象求a的取值范围.

查看试题解析
14. 已知函数 $y_{1} = x^{2} - (m + 2) x + 2 m + 3 ， y_{2} = n x + k - 2 n$ （m，n，k为常数且 $n \neq 0$ ）．

(1)、若 $y_{1}$ 的图象经过点 $A (- 1 ， 3)$ ，求该函数的表达式．

(2)、若函数 $y_{1} ， y_{2}$ 的图象始终经过同一定点M．
①求点M的坐标和k的值．
②若 $m \leq 2$ ，当 $- 1 \leq x \leq 2$ 时，总有 $y_{1} \leq y_{2}$ ，求 $m + n$ 的取值范围．

查看试题解析
15. 定义：在平面直角坐标系中，有一条直线 $x = m$ ，对于任意一个函数，作该函数自变量大于 $m$ 的部分关于直线 $x = m$ 的轴对称图形，与原函数中自变量大于或等于 $m$ 的部分共同构成一个新的函数图象，则这个新函数叫做原函数关于直线 $x = m$ 的“镜面函数”.例如：图① 是函数 $y = x + 1$ 的图象，则它关于直线 $x = 0$ 的“镜面函数”的图象如图② 所示，且它的“镜面函数”的解析式为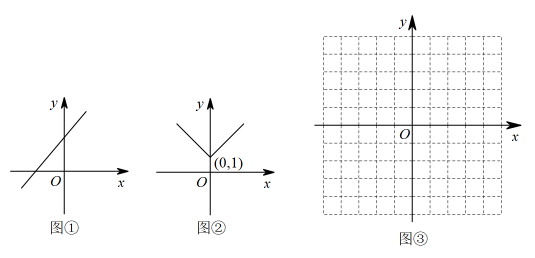 $y = {\begin{array}{l} x + 1 (x \geq 0) \\ - x + 1 (x < 0) \end{array}$ ，也可以写成 $y = | x | + 1$ .

(1)、在图③ 中画出函数 $y = - 2 x + 1$ 关于直线 $x = 1$ 的“镜面函数”的图象.

(2)、函数 $y = x^{2} - 2 x + 2$ 关于直线 $x = - 1$ 的“镜面函数”与直线 $y = - x + m$ 有三个公共点，求 $m$ 的值.

(3)、已知 $A (- 1 ， 0)$ ， $B (3 ， 0)$ ， $C (3 ， - 2)$ ， $D (- 1 ， - 2)$ ，函数 $y = x^{2} - 2 n x + 2 (n > 0)$ 关于直线 $x = 0$ 的“镜面函数”图象与矩形 $A B C D$ 的边恰好有4个交点，求n的取值范围.

查看试题解析
16. 阅读材料：一般地，对于某个函数，如果自变量x在取值范围内任取x＝a与x＝ $- a$ 时，函数值相等，那么这个函数是“对称函数”.例如，y＝x² ，在实数范围内任取x＝a时，y＝a²；当x＝ $- a$ 时，y＝ ${(- a)}^{2}$ ＝ a² ，所以y＝x²是“对称函数”.

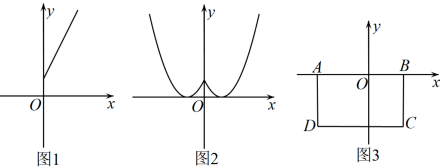(1)、函数 $y = 2 | x | + 1$ 对称函数（填“是”或“不是”）.当x≥0时， $y = 2 | x | + 1$ 的图象如图1所示，请在图1中画出x＜0时， $y = 2 | x | + 1$ 的图象.

(2)、函数 $y = x^{2} - 2 | x | + 1$ 的图象如图2所示，当它与直线y＝－x+n恰有3个交点时，求n的值.

(3)、如图3，在平面直角坐标系中，矩形ABCD的顶点坐标分别是A（－3，0），B（2，0），C（2，－3），D（－3，－3），当二次函数 $y = x^{2} - b | x | + 1$ （b>0）的图象与矩形的边恰有4个交点时，求b的取值范围.

查看试题解析