【每日15min】9二次函数与不等式—浙教版数学九（上）微专题复习

试卷更新日期：2023-10-15 类型：复习试卷

进入出卷网下载

一、选择题

1. 若二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则不等式 $a {(x - 2)}^{2} + b (x - 2) + c < 0$ 的解集为（　　）

A、 $x < 1$ 或 $x > 3$ B、 $x > 3$ C、 $x < - 1$ D、 $x < 3$ 或 $x > 5$

查看试题解析
2. 一次函数y₁=mx+n(m≠0)与二次函数y₂=ax²+bx+c(a≠0)的图象如图所示，则不等式ax²+bx+c>mx+n的解集为（）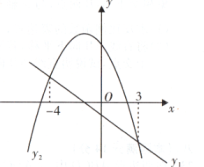

A、-4<x<3 B、x<-4 C、3-<<x<-4 D、x>3或x<-4

查看试题解析
3. 如图，抛物线y₁＝ax²+bx+c与直线y₂＝mx+n相交于点（3，0）和（0，3），若ax²+bx+c＞mx+n，则x的取值范围是（）

A、0＜x＜3 B、1＜x＜3 C、x＜0或x＞3 D、x＜1减x＞3

查看试题解析
4. 如图，二次函数y＝ax²+bx+c与反比例函数y＝ $\frac{k}{x}$ 的图象相交于点A（﹣1，y₁）、B（1，y₂）、C（3，y₃）三个点，则不等式ax²+bx+c＞ $\frac{k}{x}$ 的解集是（）

A、﹣1＜x＜0或1＜x＜3 B、x＜﹣1或1＜x＜3 C、﹣1＜x＜0或x＞3 D、﹣1＜x＜0或0＜x＜1

查看试题解析
5. 函数 $y = x {}^{2}+ b x + c$ 与 $y = x$ 的图象如图所示，有以下结论：① $b^{2} - 4 c > 0$ ② $b + c = - 1$ ③ $3 b + c + 6 = 0$ ④当 $1 < x < 3$ 时， $x^{2} + (b - 1) x + c < 0$ .其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 已知a为实数，下列命题：
①若 $a^{2} < a < \frac{1}{a}$ ，则 $0 < a < 1$ ；②若 $a < \frac{1}{a} < a^{2}$ ，则 $a < - 1$ ；③若 $\frac{1}{a} < a < a^{2}$ ，则 $a > 1$ 或 $- 1 < a < 0$ .其中真命题的个数有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
7. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴是 $x = - 2$ ，并与x轴交于A，B两点，若 $O A = 5 O B$ ，则下列结论中：① $a b c > 0$ ；② ${(a + c)}^{2} - b^{2} = 0$ ；③ $9 a + 4 c < 0$ ；④若m为任意实数，则 $a m^{2} + b m + 2 b \geq 4 a$ ，正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 若点 $P (x ， y_{1})$ 与 $Q (x ， y_{2})$ 分别是两个函数图象 $C_{1}$ 与 $C_{2}$ 上的任一点．当 $a \leq x \leq b$ 时，有-1≤y₁-y₂≤1成立，则称这两个函数在 $a \leq x \leq b$ 上是“相邻函数”．例如，点 $P (x ， y_{1})$ 与 $Q (x ， y_{2})$ 分别是两个函数 $y = 3 x + 1$ 与 $y = 2 x - 1$ 图象上的任一点，当 $- 3 \leq x \leq - 1$ 时， $y_{1} - y_{2} = (3 x + 1) - (2 x - 1) = x + 2$ ，它在 $- 3 \leq x \leq - 1$ 上，-1≤y₁-y₂≤1成立，因此这两个函数在 $- 3 \leq x \leq - 1$ 上是“相邻函数”．若函数 $y = x^{2} - x$ 与 $y = a x$ 在 $0 \leq x \leq 2$ 上是“相邻函数”，求a的取值范围（）

A、 $- 3 \leq a \leq 1$ B、 $\frac{1}{2} ≤ a ≤ 1$ C、 $a \geq \frac{1}{2}$ D、 $\frac{1}{2} \leq a \leq \frac{3}{2}$

查看试题解析

二、填空题

9. 如图，抛物线y＝ax²＋c与直线y＝kx＋b交于A（-1，m），B（2，n）两点，则不等式ax²-kx＋c＜b的解集是.

查看试题解析
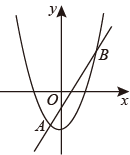10. 如图，已知抛物线 $y = a x^{2} + c$ 与直线 $y = k x + m$ 交于 $A (- 4 ， y_{1}) ， B (1 ， y_{2})$ 两点，则关于x的不等式 $a x^{2} + c \geq k x + m$ 的解集是.

查看试题解析
11. 开口向上的抛物线 $y = a x^{2} - 2 a x - 1$ 过点 $(- 1 ， y_{1})$ ， $(1 ， y_{2})$ ， $(4 ， y_{3})$ ，若 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 三个数中有且只有一个数大于零，则a的取值范围是.

查看试题解析

三、解答题

12. 已知抛物线 $y = m x^{2} - 2 m x - 3 m (m > 0)$ 与 $x$ 轴交于 $A ， B$ 两点（点A在点B左侧）.

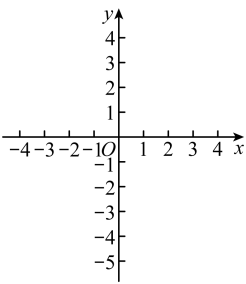(1)、抛物线对称轴为，点A坐标为；

(2)、当 $m > 0$ 时，不等式 $3 m \leq m x^{2} - 2 m x$ 的解集为；

(3)、已知点 $M (2 ， - 4) ， N (\frac{1}{2} ， - 4)$ ，连接 $M N$ 所得的线段与该抛物线有交点，求m的取值范围.

查看试题解析
13. 在平面直角坐标系xOy中，点（m – 2， y₁），（m， y₂），（2- m， y₃）在抛物线y = x²－2ax + 1上，其中m≠1且m≠2．

(1)、直接写出该抛物线的对称轴的表达式（用含a的式子表示）；

(2)、当m = 0时，若y₁= y₃ ，比较y₁与y₂的大小关系，并说明理由；

(3)、若存在大于1的实数m，使y₁＞y₂＞y₃ ，求a的取值范围．

查看试题解析
14. 已知二次函数y＝x²﹣2mx+1．记当x＝c时，函数值为y_c ，那么，是否存在实数m，使得对于满足0≤x≤1的任意实数a，b，总有y_a+y_b≥1．

查看试题解析
15.
【问题】小明在学习时遇到这样一个问题：求不等式x³+3x²-x-3>0的解集。他经历了如下思考过程：

(1)、【回顾】
如图1，在平面直角坐标系xOy中，直线y₁=ax+b与双曲线y₂= $\frac{k}{x}$ 交于A（1，3）和B（-3，-1），则不等式ax+b> $\frac{k}{x}$ 的解集是；

(2)、【探究】
将不等式x³+3x²-x-3>0按条件进行转化：

当x=0时，原不等式不成立；

当x>0时，不等式两边同除以x并移项转化为x²+3x-1> $\frac{3}{x}$ ；

当x<0时，不等式两边同除以x并移项转化为x²+3x-1< $\frac{3}{x}$ ；

构造函数，画出图象

设y₃=x²+3x-1，y₄= $\frac{3}{x}$ ，在同一坐标系中分别画出这两个函数的图象。

双曲线y₄= $\frac{3}{x}$ 如图2所示，请在此坐标系中画出抛物线y₃=x²+3x-1；（不用列表）

(3)、确定两个函数图象公共点的横坐标
观察所画两个函数的图象，猜想并通过代入函数解析式验证可知：满足y₃=y₄的所有x的值为；

(4)、【解决】借助图象，写出解集
结合“探究”中的讨论，观察两个函数的图象可知：不等式x³+3x²-x-3>0的解集为。

查看试题解析