人教版2023-2024学年九年级上学期期中数学模拟试题（七）

试卷更新日期：2023-10-15 类型：期中考试

进入出卷网下载

一、选择题

1. 方程x² = 2x的解是（）.

A、 $x = 2$ B、 $x = 0$ C、 $x_{1} = 2$ ， $x_{2} = 0$ D、 $x_{1} = - 2$ ， $x_{2} = 0$

查看试题解析
2. 若方程 $\frac{1}{2} x^{2} = 17 - 3 x$ 化成一般形式后，二次项的系数为 $\frac{1}{2}$ ，则它的一次项是（）

A、-3 B、3 C、-3x D、3x

查看试题解析
3. 已知点 $A (a ， b)$ 在第四象限，则关于x的一元二次方程 $a x^{2} + b x - 2 = 0$ 的根的情况是（）．

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定

查看试题解析
4. 已知m、n是一元二次方程 $x^{2} + 2 x - 5 = 0$ 的两个根，则 $m^{2} + m n + 3 m + n$ 的值为（）

A、 $- 1$ B、 $- 2$ C、 $- 3$ D、 $- 5$

查看试题解析
5. 将抛物线 $y = x^{2}$ 向左平移1个单位长度，得到的抛物线是（）

A、 $y = x^{2} - 1$ B、 $y = x^{2} + 1$ C、 $y = {(x - 1)}^{2}$ D、 $y = {(x + 1)}^{2}$

查看试题解析
6. 已知二次函数y＝ax²＋bx＋c的x与y的部分对应值如下表：
x
…
－3
－2
－1
0
1
3
…
y
…
－27
－13
－3
3
5
－3
…
下列结论：①a＜0；②方程ax²＋bx＋c＝3的解为x₁＝0， x₂＝2；③当x＞2时，y＜0．
其中所有正确结论的序号是（）

A、①②③ B、① C、②③ D、①②

查看试题解析
7. 能使分式方程 $\frac{k}{1 - x} + 2 = \frac{3}{x - 1}$ 有非负实数解，且使二次函数 $y = x^{2} + 2 x - k - 1$ 的图象与x轴无交点的所有整数k的积为（）

A、 $- 20$ B、20 C、 $- 60$ D、60

查看试题解析
8. 在同一平面直角坐标系中，一次函数 $y = a x + b$ 与二次函数 $y = b (x - a)^{2}$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
9. 如图所示，如图可以看作是一个菱形通过几次旋转得到的，每次可能旋转（）

A、 $30 °$ B、 $60 °$ C、 $90 °$ D、 $150 °$

查看试题解析
10. 如图，在 $△ A O B$ 中， $A O = 1 ， B O = A B = \frac{3}{2}$ ．将 $△ A O B$ 绕点O逆时针方向旋转 $90 °$ ，得到 $△ A^{'} O B^{'}$ ，连接 $A A^{'} ， B B^{'}$ ，则 $B B^{'} - A A^{'} =$ （）

A、1 B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{3}{2}$ D、 $\frac{3}{2} \sqrt{2}$

查看试题解析

二、填空题

11. 方程3x（x-1）=6（x-1）的根为.

查看试题解析
12. $x = 1$ 是关于x的一元二次方程 $x^{2} + a x + 2 b = 0$ 的解，则 $a + 2 b =$ ．

查看试题解析
13. 已知函数 $y = - {(x - 1)}^{2} + h$ 的图像过点 $A (3 ， a)$ 和 $B (m ， b)$ ，且 $a < b$ ，则 $m$ 的取值范围是．

查看试题解析
14. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的大致图象如图所示，顶点坐标为 $(- 2 ， - 9 a)$ ，下列结论：① $a b c > 0$ ；② $16 a - 4 b + c < 0$ ；③若方程 $a x^{2} + b x + c = - 1$ 有两个根 $x_{1}$ 和 $x_{2}$ ，且 $x_{1} < x_{2}$ ，则 $- 5 < x_{1} < x_{2} < 1$ ；④ $a^{2} + a b + c$ 的最小值为 $- \frac{5}{4}$ ．其中正确结论的是．

查看试题解析
15. 如图，P是正方形ABCD内一点，且点P到点B、C、D的距离分别为 $2 \sqrt{3}$ 、 $\sqrt{2}$ 、4，则 $∠ B P C$ 的度数为

查看试题解析

三、解答题

16. 解方程： $x^{2} + 2 x - 8 = 0$

查看试题解析
17. 关于x的一元二次方程（x－2）（x－3）＝m有两个不相等的实数根x₁ ， x₂ ，求m的取值范围；若x₁ ， x₂满足等式x₁x₂－x₁－x₂＋1＝0，求m的值．

查看试题解析
18. 如图，以一定的速度将小球沿与地面成一定角度的方向击出时，小球的飞行路线是一条抛物线．若不考虑空气阻力，小球的飞行高度h(单位：m)与飞行时间t(单位：s)之间具有函数关系：h=-5t²+20t，求小球飞行高度达到最高时的飞行时间．

查看试题解析
19. 如图，在 $△ A B C$ 中， $A B = 2$ ， $B C = 3.6$ ， $∠ B = 60 °$ ，将 $△ A B C$ 绕点A按顺时针旋转一定角度得到 $△ A D E$ ，当点B的对应点D恰好落在BC边上时，求CD的长.

查看试题解析

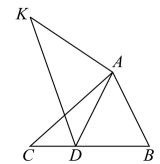
四、综合题

20. 若关于x的方程mx²-2x+3＝0有两个实数根.

(1)、求m的取值范围；

(2)、方程有两个相等的实数根时，求出方程的根.

查看试题解析
21. 如图，抛物线 $y = a x^{2} + 3 x + c (a \neq 0)$ 与 $x$ 轴交于点 $A (- 2 ， 0)$ 和点 $B$ ，与 $y$ 轴交于点 $C (0 ， 8)$ ，点 $P$ 为直线 $B C$ 上方抛物线上的动点，连接 $C P$ ， $P B$ ，直线 $B C$ 与抛物线的对称轴 $l$ 交于点 $E$ .

(1)、求抛物线的解析式；

(2)、求 $△ B C P$ 的面积最大值；

查看试题解析
22. 今年以来，某市接待游客人数逐月增加，据统计，八月份和十月份到某景区游玩的游客人数分别为4万人和5.76万人．

(1)、求八月到十月该景区游客人数平均每月的增长率；

(2)、若该景区仅有A，B两个景点，售票处出示的三种购票方式如表所示：
购票方式
甲
乙
丙
可游玩景点
A
B
A和B
门票价格
100元/人
80元/人
160元/人
据预测，十一月份选择甲、乙、丙三种购票方式的人数分别有2万人、3万人和2万人，并且当甲、乙两种门票价格不变时，丙种门票价格每下降1元，将有600名原计划购买甲种门票的游客和400名原计划购买乙种门票的游客改为购买丙种门票．设十一月份景区门票总收入为W万元，丙种门票下降m元，请写出W与m之间的表达式，并求出要想让十一月份门票总收入达到798万元，丙种门票应该下降多少元？

查看试题解析
23. 如图1， $△ A O B$ 中， $O A = O B = 6$ ，将 $△ A O B$ 绕点O逆时针旋转得到 $△ C O D$ ， $O C$ 与 $A B$ 交于点G， $C D$ 分别交 $O B$ 、 $A B$ 于点E、F．

(1)、求证： $∠ A = ∠ D$ ；

(2)、求证： $△ A O G ≌ △ D O E$ ；

(3)、如图2，当旋转到 $∠ A O D = 180 °$ 时，此时恰好 $O B ⊥ C D$ ，求 $C D$ 的长．

查看试题解析

购票方式	甲	乙	丙
可游玩景点	A	B	A和B
门票价格	100元/人	80元/人	160元/人

x	…	－3	－2	－1	0	1	3	…
y	…	－27	－13	－3	3	5	－3	…