【每日15min】8二次函数图象与一元二次方程—浙教版数学九(上)微专题复习
试卷更新日期:2023-10-15 类型:复习试卷
一、选择题
-
1. 如图,抛物线的对称轴是直线 , 关于的方程的一个根为 , 则另一个根为( )
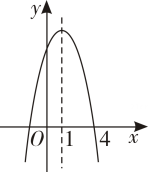 A、
A、
B、
C、
D、2. 如图,抛物线y=ax2+bx+c交x轴于(-1,0),(3,0),则下列判断错误的是( ).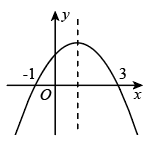 A、图象的对称轴是直线x=1 B、当x>1时,y随x的增大而减小 C、一元二次方程ax2+bx+c=0的两个根分别是-1和3 D、当y<0时,x<-13. 已知抛物线与轴有两个不同的交点,则关于的一元二次方程根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定4. 关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根分别为-1和5,则二次函数y=ax2+bx+c(a≠0)的对称轴是( )A、x=-3 B、x=-1 C、x=2 D、x=35. 根据下表的对应值,试判断一元二次方程 的一解的取值范围是( )
A、图象的对称轴是直线x=1 B、当x>1时,y随x的增大而减小 C、一元二次方程ax2+bx+c=0的两个根分别是-1和3 D、当y<0时,x<-13. 已知抛物线与轴有两个不同的交点,则关于的一元二次方程根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定4. 关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根分别为-1和5,则二次函数y=ax2+bx+c(a≠0)的对称轴是( )A、x=-3 B、x=-1 C、x=2 D、x=35. 根据下表的对应值,试判断一元二次方程 的一解的取值范围是( )3.23
3.24
3.25
3.26
-0.06
-0.02
0.03
0.07
A、 B、 C、 D、6. 二次函数y=﹣x2+mx的图象如图,对称轴为直线x=2,若关于x的一元二次方程﹣x2+mx﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是( )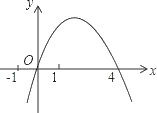 A、t>﹣5 B、﹣5<t<3 C、3<t≤4 D、﹣5<t≤47. 设一元二次方程(x-1)(x-2)=m(m>0)的两实根分别为α,β,且α<β,则α,β满足( )A、1<α<β<2 B、1<α<2<β C、α<1<β<2 D、α<1且β>28. 小李同学在求一元二次方程﹣2x2+4x+1=0的近似根时,先在直角坐标系中使用软件绘制了二次函数y=﹣2x2+4x+1的图象(如图),接着观察图象与x轴的交点A和B的位置,然后得出该一元二次方程两个根的范围是﹣1<x1<0,2<x2<3,小李同学的这种方法主要运用的数学思想是( )
A、t>﹣5 B、﹣5<t<3 C、3<t≤4 D、﹣5<t≤47. 设一元二次方程(x-1)(x-2)=m(m>0)的两实根分别为α,β,且α<β,则α,β满足( )A、1<α<β<2 B、1<α<2<β C、α<1<β<2 D、α<1且β>28. 小李同学在求一元二次方程﹣2x2+4x+1=0的近似根时,先在直角坐标系中使用软件绘制了二次函数y=﹣2x2+4x+1的图象(如图),接着观察图象与x轴的交点A和B的位置,然后得出该一元二次方程两个根的范围是﹣1<x1<0,2<x2<3,小李同学的这种方法主要运用的数学思想是( )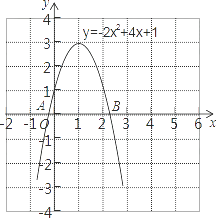 A、公理化 B、类比思想 C、数形结合 D、模型思想
A、公理化 B、类比思想 C、数形结合 D、模型思想二、填空题
-
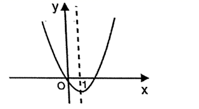
9. 二次函数 的图象如图,对称轴为直线 .若关于 的一元二次方程 ( 为实数)在 的范围内解,则 的取值范围是 .
 10. 已知关于 的一元二次方程 的一个根是 ,且二次函数 的对称轴是直线 ,则此方程 的另一个解为.11. 在关于的 二次函数中,自变量 可以取任意实数,下表是自变量 与函数 的几组对应值:
10. 已知关于 的一元二次方程 的一个根是 ,且二次函数 的对称轴是直线 ,则此方程 的另一个解为.11. 在关于的 二次函数中,自变量 可以取任意实数,下表是自变量 与函数 的几组对应值:…
1
2
3
4
5
6
7
8
…
…
-1.78
-3.70
-4.42
-3.91
-2.20
4.88
10.27
…
根据以上信息,关于 的一元二次方程 的两个实数根中,其中的一个实数根约等于(结果保留小数点后一位).
12. 的顶点坐标(-1,-3.2)及部分图象(如图所示),由图象可知关于x的一元二次方程 的两个根分别是x1=1.3和x2= .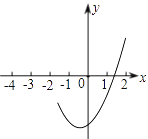
三、解答题
-
13. 利用二次函数的图象求下列一元二次方程的根.(1)、4x2﹣8x+1=0(2)、x2﹣2x﹣5=0(3)、2x2﹣6x+3=0(4)、x2﹣x﹣1=014. 已知关于x的一元二次方程: .(1)、当时,解方程:(2)、若的一个解是 , 求k;(3)、若抛物线与x轴无交点,试确定k的取值范围.15. 小明在复习数学知识时,针对“求一元二次方程的解”整理了以下几种方法,请你将有关内容补充完整:
例题:求一元二次方程x2﹣x﹣1=0的两个解.
(1)、解法一:(1)选择合适的一种方法(公式法、配方法、分解因式法).(2)、(2)解法二:利用二次函数图象与坐标轴的交点求解,如图(1)所示,①把方程x2-x-1=0的解看成是二次函数y= 的图象与x 轴交点的横坐标,即x1 , x2就是方程的解。②画出这两个函数的图象 ,用x1 , x2在x轴上标出方程的解。