【每日15min】7二次函数图象与坐标轴—浙教版数学九（上）微专题复习

试卷更新日期：2023-10-15 类型：复习试卷

进入出卷网下载

一、选择题

1. 已知二次函数 $y = (k - 3) x^{2} + 2 x + 1$ 的图象与x轴有交点，则k的取值范围是（）

A、 $k \leq 4$ 且 $k \neq 3$ B、 $k < 4$ 且 $k \neq 3$ C、 $k < 4$ D、 $k \geq 4$

查看试题解析
2. 已知抛物线 $y = (x - 3)^{2} + c$ 经过点 $A (2 ， 0)$ ，则该抛物线与 $x$ 轴的另一个交点是（）

A、 $(3 ， 0)$ B、 $(4 ， 0)$ C、 $(- 8 ， 0)$ D、 $(- 4 ， 0)$

查看试题解析
3. 抛物线 $y = x^{2} - 2 x$ 的图象与x轴交点的横坐标分别是（）

A、0，1 B、1，2 C、0，2 D、－1，－2

查看试题解析
4. 二次函数 $y = x^{2} - 3 x + 1$ 的图象与y轴的交点坐标是（）

A、 $(0 ， 0)$ B、 $(0 ， 1)$ C、 $(0 ， - 3)$ D、 $(3 ， 0)$

查看试题解析
5. 关于二次函数 $y = x^{2} - k x + k - 1 (k \neq 0)$ ，则下列正确的是（）

A、函数图象与x轴总有两个不同的交点 B、若函数图象与x轴正半轴交于不同的两点，则 $k > 0$ C、不论k为何值，若将函数图象向左平移1个单位，则图像经过原点 D、当 $x \geq 1$ 时，y随x的增大而增大，则 $k < 2$

查看试题解析
6. 抛物线y＝ax²＋bx＋c上部分点的横坐标x，纵坐标y的对应值如下表：
x
…
-2
-1
0
1
2
…
y
…
0
4
6
6
4
…
从表中可知，下列说法中正确的是（）

A、抛物线的对称轴是直线x＝0 B、抛物线与x轴的一个交点为（3，0） C、函数y＝ax²＋bx＋c的最大值为6 D、在对称轴右侧，y随x增大而增大

查看试题解析
7. 已知抛物线 $y = x^{2} - 2 x - 1$ 与x轴的一个交点为 $(m ， 0)$ ，则代数式 $m^{2} - 2 m + 2021$ 的值为（）

A、2021 B、2020 C、2022 D、2023

查看试题解析
8. 能使分式方程 $\frac{k}{1 - x} + 2 = \frac{3}{x - 1}$ 有非负实数解，且使二次函数 $y = x^{2} + 2 x - k - 1$ 的图象与x轴无交点的所有整数k的积为（）

A、 $- 20$ B、20 C、 $- 60$ D、60

查看试题解析

二、填空题

9. 抛物线 $y = x^{2} + 4 x + 3$ 在 $x$ 轴上截得的线段的长度是．

查看试题解析
10. 已知抛物线 $y = x^{2} + x + m$ 与 $y$ 轴的交点在原点下方，则整数 $m$ 的值可以是 $. ($ 写出一个符合条件的值即可 $)$

查看试题解析
11. 已知抛物线 $y = a x^{2} + 3 a x + c (a \neq 0)$ ，若抛物线恒在 $x$ 轴下方，且符合条件的整数 $a$ 只有三个，则实数 $c$ 的最小值为.

查看试题解析
12. 已知抛物线 $y = - x^{2} - 2 x + 3$ 与 $y$ 轴交于点 $C$ ，点 $P$ 是抛物线上的动点， $D (0 ， 1)$ ，若 $△ P C D$ 是以 $C D$ 为底的等腰三角形，则点 $P$ 的坐标为．

查看试题解析

三、解答题

13. 已知二次函数 $y = a x^{2} + b x - 1 (a \neq 0)$ 的图像与 $x$ 轴交于点 $(- 1 ， 0)$ 和 $(4 ， 0)$ ．写出它与 $y$ 轴交点的坐标，并求出它的解析式．

查看试题解析
14. 已知二次函数 $y = m x^{2} - (m + n) x + n (m < 0)$ ， $A (- 1 ， 0) ， B (0 ， - 1) ， C (0 ， 1)$ .

(1)、若二次函数的图象经过A，C两点，求二次函数的解析式.

(2)、若二次函数图象与y轴正半轴有交点，试判断二次函数的图象与x轴的交点个数，并说明理由.

(3)、若二次函数图象经过点C，设P $(a ， b)$ 为二次函数图象上的一个动点，当 $- 3 < a < 0$ 时，点P关于x轴的对称点都在直线 $A B$ 的下方，求m的取值范围.

查看试题解析

四、实践探究题

15. 《函数的图象与性质》拓展学习片段展示：

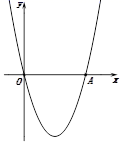
(1)、（问题）
如图①，在平面直角坐标系中，抛物线y=a（x-2）²-4经过原点O，与x轴的另一个交点为A，则a= ，点A的坐标为 .

(2)、（操作）
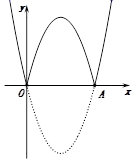
将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方，如图②.直接写出翻折后的这部分抛物线对应的函数解析式：.

(3)、（探究）
在图②中，翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象，则新图象对应的函数y随x的增大而增大时，x的取值范围是.

(4)、（应用）结合上面的操作与探究，继续思考：如图③，若抛物线y=（x-h）²-4与x轴交于A，B两点（A在B左），将抛物线在x轴下方的部分沿x轴翻折，同样，也得到了一个“W”形状的新图象.
求A、B两点的坐标；（用含h的式子表示）

(5)、当1＜x＜2时，若新图象的函数值y随x的增大而增大，求h的取值范围.

查看试题解析

x	…	-2	-1	0	1	2	…
y	…	0	4	6	6	4	…