人教版2023-2024学年九年级上学期期中数学模拟试题（五）

试卷更新日期：2023-10-15 类型：期中考试

进入出卷网下载

一、选择题

1. 用配方法解方程 $x^{2} + 4 x + 1 = 0$ 时，配方结果正确的是（）

A、 ${(x - 2)}^{2} = 5$ B、 ${(x - 2)}^{2} = 3$ C、 ${(x + 2)}^{2} = 5$ D、 ${(x + 2)}^{2} = 3$

查看试题解析
2. 关于x的方程 $(a - 1) x^{2} + 3 x - 2 = 0$ 是一元二次方程的条件是（）

A、 $a \neq 0$ B、 $a = 1$ C、 $a \neq 1$ D、a为任意实数

查看试题解析
3. 直角三角形两直角边是方程 $x^{2} - 8 x + 14 = 0$ 的两根，则它的斜边为（）

A、8 B、7 C、6 D、 $2 \sqrt{7}$

查看试题解析
4. 若二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则不等式 $a {(x - 2)}^{2} + b (x - 2) + c < 0$ 的解集为（　　）

A、 $x < 1$ 或 $x > 3$ B、 $x > 3$ C、 $x < - 1$ D、 $x < 3$ 或 $x > 5$

查看试题解析
5. 将抛物线y＝-x²向上平移2个单位，则得到的抛物线表达式为（　　）

A、y＝-（x+2）² B、y＝-（x-2）² C、y＝-x²-2 D、y＝-x²+2

查看试题解析
6. 已知(-4，y₁)，(2.5，y₂)，(5，y₃)是抛物线y＝-3x²-6x+m上的点，则y₁、y₂、y₃的大小关系是（）

A、y₁＞y₂＞y₃ B、y₃＞y₂＞y₁ C、y₁＞y₃＞y₂ D、y₂＞y₁＞y₃

查看试题解析
7. 二次函数 $y = (k + 1) x^{2} - 4 x + 1$ 的图象与x轴有两个交点，那么k的取值范围是（）

A、 $k \leq 3$ 且 $k \neq$ -1 B、 $k < 3$ 且 $k \neq$ -1 C、 $k \leq 3$ D、 $k < 3$

查看试题解析
8. 若P(x，3)与点Q(4，y)关于原点对称，则xy的值是(　　)

A、12 B、-12 C、64 D、-64

查看试题解析
9. 2022贵阳国际车展以“潮黔看 $\cdot$ 驭未来”为主题，汇聚80余个汽车品牌，为市民带来更炫酷、更极致的观展体验.下面是此次车展中的几个车标，其中是中心对称图形而不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在正方形ABCD中，AB＝4，点M在CD的边上，且DM＝1，△AEM与△ADM关于AM所在的直线对称，将△ADM按顺时针方向绕点A旋转90°得到△ABF，连接EF，则线段EF的长为（　　）

A、3 B、2 $\sqrt{3}$ C、5 D、 $\sqrt{13}$

查看试题解析

二、填空题

11. 已知 $x_{1}$ 、 $x_{2}$ 是方程 $x^{2} - 2 x - 1 = 0$ 的两根，则 $x_{1}^{2} + x_{2}^{2} =$ .

查看试题解析
12. 设a、b为 $x^{2} + x - 2021 = 0$ 的两个实数根，则 $a^{3} + a^{2} + 3 a + 2024 b$ ＝.

查看试题解析
13. 已知方程 $a x^{2} + b x + c = 0$ 的两个根为1和-3，则抛物线 $y = a x^{2} + b x + c$ 的对称轴为直线.

查看试题解析
14. 若点A（-2，y₁）和B（1，y₂）是二次函数 $y ＝ - x^{2} - k$ 图象上的两点，则y₁y₂（填“＜”“＝”或“＞”）.

查看试题解析
15. 如图，将右边的图案变成左边的图案，是通过变化得到的.

查看试题解析

三、解答题

16. 阅读下面的材料，并完成相应的任务．
材料：解含绝对值的方程： $x^{2} - 5 | x | - 6 = 0$ ．

解：分两种情况：

（ 1 ）当 $x \geq 0$ 时，原方程可化为： $x^{2} - 5 x - 6 = 0$ ，解得 $x_{1} = 6$ ， $x_{2} = - 1$ （舍去）；

（ 2 ）当 $x < 0$ 时，原方程可化为： $x^{2} + 5 x - 6 = 0$ ，解得 $x_{1} = - 6$ ， $x_{2} = 1$ （舍去）．

综上所述：原方程的解是 $x_{1} = 6$ ， $x_{2} = - 6$ ．任务：请参照上述方法解方程： $x^{2} - | x | - 2 = 0$ ．

查看试题解析
17. 已知关于x的一元二次方程 $m x^{2} - (m + 2) x + \frac{m}{4} = 0$ 两个不相等的实数根 $x_{1}$ ， $x_{2}$ ，若 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = 4 m$ ，求m的值．

查看试题解析
18. 某农场拟建两间矩形种牛饲养室，饲养室的一面靠现有墙（墙长＞50m），中间用一道墙隔开（如图），已知计划中的建筑材料可建围墙的总长为50m，设两饲养室合计长x（m），总占地面积为y（m²）

(1)、求y关于x的函数表达式和自变量的取值范围；

(2)、若要使两间饲养室占地总面积达到200m² ，则x为多少？占地总面积有可能达到210m²吗？

查看试题解析
19. 如图，将矩形 $A B C D$ 绕点A顺时针旋转得到矩形 $A B^{^{'}} C^{^{'}} D^{^{'}}$ ，点C的对应点 $C^{'}$ 恰好落在 $C B$ 的延长线上，求证： $B C = B C^{'}$ ．

查看试题解析

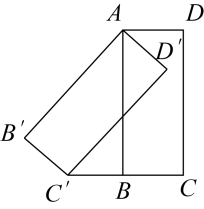
四、综合题

20. 已知方程 $2 x^{2} - k x - 6 = 0$ 的一个根为 $x_{1} = - 2$ .

(1)、求 $k$ 的值；

(2)、设方程的另一个根为 $x_{2}$ ，求 ${x_{1}}^{2} \cdot x_{2} + x_{1} \cdot {x_{2}}^{2}$ 的值.

查看试题解析
21. 已知关于x的方程 $x^{2} - (k + 2) x + 2 k = 0$

(1)、求证：无论k取何值，该方程总有实数根；

(2)、若等腰 $△ A B C$ 的一边长 $a = 1$ ，另两边b、c恰好是该方程的两个根，求三角形另外两边的长.

查看试题解析
22. 如图，一名男生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ．求：

(1)、铅球在行进中的最大高度；

(2)、该男生将铅球推出的距离是多少m？

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ A B C = 9 0^{∘}$ ，将 $R t △ A B C$ 绕点 $C$ 顺时针方向旋转 $60 °$ 得到 $△ D E C$ 点 $E$ 在 $A C$ 上，再将 $R t △ A B C$ 沿着 $A B$ 所在直线翻转 $18 0^{∘}$ 得到 $△ A B F$ ，连接 $A D$ .

(1)、求证：四边形 $A F C D$ 是菱形；

(2)、连接 $B E$ 并延长 $A D$ 交于 $G$ 连接 $C G ，$ 请问：四边形 $A B C G$ 是什么特殊四边形？为什么？

查看试题解析