人教版2023-2024学年八年级上学期期中数学模拟试题(七)
试卷更新日期:2023-10-15 类型:期中考试
一、选择题
-
1. 已知三角形三边长分别为 , , , 且为奇数,则这样的三角形有( )A、个 B、个 C、个 D、个2. 如图,中, , 为上一点,于点 , 下列说法中,错误的是( )
 A、中,是上的高 B、中,是上的高 C、中,是上的高 D、中,是上的高3. 如图,在四边形中, , 的平分线与的平分线交于点 , 则( )
A、中,是上的高 B、中,是上的高 C、中,是上的高 D、中,是上的高3. 如图,在四边形中, , 的平分线与的平分线交于点 , 则( ) A、 B、 C、 D、4. 如图,空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是( )
A、 B、 C、 D、4. 如图,空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是( ) A、三角形两边之差小于第三边 B、三角形两边之和大于第三边 C、垂线段最短 D、三角形的稳定性5. 如图,点E,点F在直线AC上,AE=CF,AD=CB,下列条件中不能判断△ADF≌△CBE的是( )
A、三角形两边之差小于第三边 B、三角形两边之和大于第三边 C、垂线段最短 D、三角形的稳定性5. 如图,点E,点F在直线AC上,AE=CF,AD=CB,下列条件中不能判断△ADF≌△CBE的是( ) A、AD∥BC B、BE∥DF C、BE=DF D、∠A=∠C6. 已知,如图,是内部的一条射线,是射线上任意点, , , 下列条件中: , , , , 能判定是的角平分线的有( )
A、AD∥BC B、BE∥DF C、BE=DF D、∠A=∠C6. 已知,如图,是内部的一条射线,是射线上任意点, , , 下列条件中: , , , , 能判定是的角平分线的有( )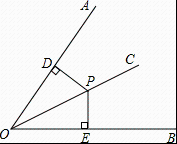 A、个 B、个 C、个 D、个7. 如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( )
A、个 B、个 C、个 D、个7. 如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( ) A、 B、 C、 D、8. 如图,在中, , , 平分交于点 , 交于点 , 下列四个结论:
A、 B、 C、 D、8. 如图,在中, , , 平分交于点 , 交于点 , 下列四个结论:
;
点在的垂直平分线上;
图中共有个等腰三角形;
≌;
其中正确的结论有( )
A、个 B、个 C、个 D、个9. 下列标志是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 10. 在平面直角坐标系中,点关于轴对称的点的坐标是( )A、 B、 C、 D、
10. 在平面直角坐标系中,点关于轴对称的点的坐标是( )A、 B、 C、 D、二、填空题
-
11. 如图,小亮从点处出发,前进米后向右转 , 再前进米后又向右转 , 这样走次后恰好回到出发点处,小亮走出的这个边形的周长是 米
 12. 如图,一副直角三角板中, , , , 现将直角顶点按照如图方式叠放,点在直线上方,且 , 能使三角形有一条边与平行的所有的度数为 .
12. 如图,一副直角三角板中, , , , 现将直角顶点按照如图方式叠放,点在直线上方,且 , 能使三角形有一条边与平行的所有的度数为 .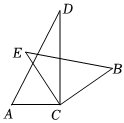 13. 如图,在中, , , 是的平分线,于点若 , , 则的周长为 .
13. 如图,在中, , , 是的平分线,于点若 , , 则的周长为 . 14. 如图,C为线段AE上一动点(不与A,E重合),在AE同侧分别作等边△ABC和等边△ECD,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,则有以下五个结论:①AD=BE;②PQ∥AE;③△PCQ为轴对称图形;④DP=DE;⑤∠AOB=60°.以上结论正确的是(填序号).
14. 如图,C为线段AE上一动点(不与A,E重合),在AE同侧分别作等边△ABC和等边△ECD,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,则有以下五个结论:①AD=BE;②PQ∥AE;③△PCQ为轴对称图形;④DP=DE;⑤∠AOB=60°.以上结论正确的是(填序号). 15. 若等腰三角形一腰上的高和另一腰的夹角为20°,则该三角形的一个底角为°
15. 若等腰三角形一腰上的高和另一腰的夹角为20°,则该三角形的一个底角为°三、解答题
-
16. 如图,是的边上的一点, , , .
 (1)、求的度数.(2)、求的度数.17. 如图,已知是上一点,是上的一点,、相交于点 , , , .
(1)、求的度数.(2)、求的度数.17. 如图,已知是上一点,是上的一点,、相交于点 , , , . (1)、的度数;(2)、的度数.18. 如图,点、、、在一条直线上, , , 求证: .
(1)、的度数;(2)、的度数.18. 如图,点、、、在一条直线上, , , 求证: . 19. 如图,在中, , 平分 , 于 , 若 , 求的度数.
19. 如图,在中, , 平分 , 于 , 若 , 求的度数.
四、综合题
-
20. 如图,点在第一象限,点B(0,-4)在y轴负半轴上.
 (1)、求△AOB的面积;(2)、坐标轴上是否存在点D(不和点B重合),使S△AOD=S△AOB?若存在,请直接写出D点坐标;若不存在,请说明理由;(3)、若OA与x轴正半轴形成的夹角为60°,射线OA绕O点以每秒4°的速度顺时针旋转到OA′,射线BO绕B点以每秒10°的速度顺时针旋转到BO',当BO转动一周时两者都停止运动.若两射线同时开始运动,在旋转过程中,经过多长时间,OA′∥BO'?21. 如图,△在平面直角坐标系中的位置如图,其中点 , 点分别在轴和轴上,且和满足: , 若点在第四象限, , 且 .
(1)、求△AOB的面积;(2)、坐标轴上是否存在点D(不和点B重合),使S△AOD=S△AOB?若存在,请直接写出D点坐标;若不存在,请说明理由;(3)、若OA与x轴正半轴形成的夹角为60°,射线OA绕O点以每秒4°的速度顺时针旋转到OA′,射线BO绕B点以每秒10°的速度顺时针旋转到BO',当BO转动一周时两者都停止运动.若两射线同时开始运动,在旋转过程中,经过多长时间,OA′∥BO'?21. 如图,△在平面直角坐标系中的位置如图,其中点 , 点分别在轴和轴上,且和满足: , 若点在第四象限, , 且 . (1)、请直接写出点和点的坐标;(2)、求点的坐标;(3)、若交轴于 , 交轴于 , 是线段上一点,且 , 连 , 求证: .
(1)、请直接写出点和点的坐标;(2)、求点的坐标;(3)、若交轴于 , 交轴于 , 是线段上一点,且 , 连 , 求证: .

