【每日15min】4二次函数图象与系数的关系—浙教版数学九(上)微专题复习
试卷更新日期:2023-10-15 类型:复习试卷
一、选择题
-
1. 已知二次函数的图像如图所示,那么下列四个结论中,错误的是( )
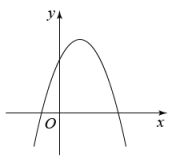 A、 B、 C、 D、2. 已知: , 且 , 则二次函数的图象可能是下列图象中的( )A、
A、 B、 C、 D、2. 已知: , 且 , 则二次函数的图象可能是下列图象中的( )A、 B、
B、 C、
C、 D、
D、 3. 若抛物线y=x2+x+m-1(m是常数)经过第一、二、三象限,则m的取值范围是( )A、m>1 B、m< C、1<m< D、1≤m<4. 如图,抛物线的对称轴是直线 , 并与x轴交于A,B两点,且 , 下列结论错误的是( )
3. 若抛物线y=x2+x+m-1(m是常数)经过第一、二、三象限,则m的取值范围是( )A、m>1 B、m< C、1<m< D、1≤m<4. 如图,抛物线的对称轴是直线 , 并与x轴交于A,B两点,且 , 下列结论错误的是( ) A、 B、 C、 D、若m为任意实数,则5. 如果二次函数的图象如图所示,那么一次函数的图象大致是( )
A、 B、 C、 D、若m为任意实数,则5. 如果二次函数的图象如图所示,那么一次函数的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 二次函数的图象如图所示,则一次函数的图象和反比例函数的图象在同一平面直角坐标系中大致为( )
6. 二次函数的图象如图所示,则一次函数的图象和反比例函数的图象在同一平面直角坐标系中大致为( )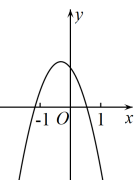 A、
A、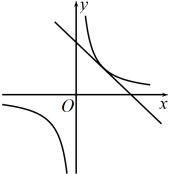 B、
B、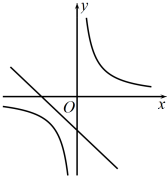 C、
C、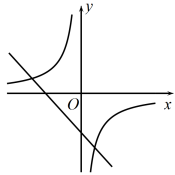 D、
D、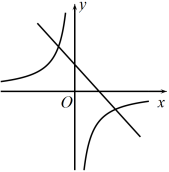 7. 已知抛物线的图像经过第四象限,则m的取值范围是( )A、 B、 C、 D、8. 已知二次函数的图象如图所示,下列结论:
7. 已知抛物线的图像经过第四象限,则m的取值范围是( )A、 B、 C、 D、8. 已知二次函数的图象如图所示,下列结论:①;②;③;④ , 其中正确的是( )
 A、①④ B、②④ C、②③ D、①③④
A、①④ B、②④ C、②③ D、①③④二、填空题
-
9. 若二次函数的图像开口向下,则m的值为 .10. 抛物线有最高点,那么k的取值范围是 .11. 二次函数的图象如图所示,则m的取值范围是 .
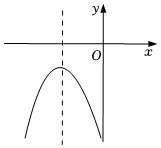 12. 已知点与点都在二次函数的图象上,若 , 则a的取值范围为 .13. 抛物线y1=ax2-1与y2=x2-x,当0≤x≤1时,|y1-y2|≤1,则a的取值范围是
12. 已知点与点都在二次函数的图象上,若 , 则a的取值范围为 .13. 抛物线y1=ax2-1与y2=x2-x,当0≤x≤1时,|y1-y2|≤1,则a的取值范围是三、综合题
