2023-2024学年北师大版数学八年级上册 5.7用二元一次方程组确定一次函数表达式同步练习（提升卷）

试卷更新日期：2023-10-15 类型：同步测试

进入出卷网下载

一、选择题

1. 若直线y=-x+m与直线y=2x+4的交点在第二象限，则m的取值范围是（）

A、 $- 2 < m < 4$ B、 $- 2 < m < 3$ C、 $- 1 < m < 3$ D、 $- 1 < m < 4$

查看试题解析
2. 一次函数 $y = k x + 5 (k \neq 0)$ 的图象与正比例函数 $y = m x (m \neq 0)$ 的图象都经过点（－3，2），则方程组 ${\begin{array}{l} y = k x + 5 \\ y = m x \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = - 3 \\ y = - 2 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = - 3 \end{array}$ D、 ${\begin{array}{l} x = - 3 \\ y = 2 \end{array}$

查看试题解析
3. 如图，直线 $l_{1} ： y = 3 x + 1$ 与直线 $l_{2} ： y = m x + n$ 相交于点 $P (1 ， b)$ ，则关于x，y的方程组 ${\begin{array}{l} y = 3 x + 1 \\ y = m x + n \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 1 \\ y = 4 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = 2.5 \end{array}$

查看试题解析
4. 如图，点 $A$ 的坐标为 $(- 1 ， 0)$ ，直线 $y = x - 2$ 与 $x$ 轴交于点 $C$ ，与 $y$ 轴交于点 $D$ ，点 $B$ 在直线 $y = x - 2$ 上运动．当线段 $A B$ 最短时，求点 $B$ 的坐标（）

A、 $(\frac{1}{2} ， - \frac{3}{2})$ B、 $(1 ， - 1)$ C、 $(\frac{1}{3} ， - \frac{5}{3})$ D、 $(0 ， - 2)$

查看试题解析
5. 如图，一次函数y＝2x＋1的图象与y＝kx＋b的图象相交于点A，则方程组 ${\begin{array}{l} 2 x - y = - 1 \\ k x - y = - b \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 3 \\ y = 7 \end{array}$ B、 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$

查看试题解析
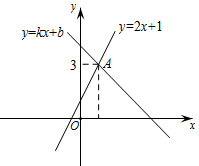6. 在平面直角坐标系内，一次函数 $y = k_{1} x + b_{1}$ 与 $y = k_{2} x + b_{2}$ 的图象如图所示，则关于x，y的方程组 ${\begin{array}{l} y - k_{1} x = b_{1} \\ y - k_{2} x = b_{2} \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = - 2 \\ y = - 3 \end{array}$ B、 ${\begin{array}{l} x = - 4 \\ y = - 2 \end{array}$ C、 ${\begin{array}{l} (x = - 2 \\ y = - 4 \end{array}$ D、 ${\begin{array}{l} x = 0 \\ y = - 3 \end{array}$

查看试题解析
7. 已知一次函数y＝k₁x+b₁和一次函数y₁＝k₂x+b₂的自变量x与因变量y₁ ， y₂的部分对应数值如表所示，则关于x、y的二元一次方程组 ${\begin{array}{l} y = k_{1} x + b_{1} \\ y = k_{2} x + b_{2} \end{array}$ 的解为（　　）
x
…
﹣2
﹣1
0
1
2
…
y₁
…
﹣1
0
1
2
3
…
y₂
…
﹣5
﹣3
﹣1
1
3
…

A、 ${\begin{array}{l} x = - 5 \\ y = - 2 \end{array}$ B、 ${\begin{array}{l} x = 4 \\ y = 5 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ D、 ${\begin{array}{l} x = - 1 \\ y = - 3 \end{array}$

查看试题解析
8. 如图，在平面直角坐标系中，一次函数y＝kx+b（k≠0）和y＝mx+n（m≠0）相交于点(2，﹣1)，则关于x，y的方程组 ${\begin{array}{l} k x = y - b \\ m x + n = y \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$

查看试题解析
9. 下列图象中，以方程﹣2x＋y﹣2＝0的解为坐标的点组成的图象是（）

A、 B、 C、 D、

查看试题解析
10. 已知直线l₁：y=kx+b与直线l₂：y=-2x+4交于点C（m，2），则方程组 ${\begin{array}{l} y = k x + b \\ y = - 2 x + 4 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$

查看试题解析

二、填空题

11. 如图，在平面直角坐标系中，直线 $y = 2 x + 1$ 与直线 $y = - 3 x + m$ 相交于点 $P$ ，若点 $P$ 的横坐标为1，则关于 $x ， y$ 的二元一次方程组 ${\begin{cases} y = 2 x + 1 \\ y = - 3 x + m \end{cases}$ 的解是。

查看试题解析
12. 已知一次函数 $y = 3 x - 1$ 与 $y = 2 x$ 图象的交点是 $(1 ， 2)$ ，则方程组 ${\begin{array}{l} 3 x - y = 1 \\ 2 x - y = 0 \end{array}$ 的解是．

查看试题解析
13. 已知一次函数y＝ax+b和y＝kx的图象交于点P（﹣4，2），则关于x、y的二元一次方程组 ${\begin{array}{l} y = a x + b \\ y = k x \end{array}$ 的解是.

查看试题解析
14. 如图，直线 $l_{1} ： y = x + 1$ 与直线 $l_{2} ： y = m x + n$ 相交于点 $P (1 ， b)$ ，则关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} y = x + 1 \\ y = m x + n \end{array}$ 的解为．

查看试题解析
15. 如图，已知直线l₁：y＝3x+1和直线l₁：y＝mx+n交于点P（1，b），则关于x，y的二元一次方程组 ${\begin{matrix} y = m x + n \\ y = 3 x + 1 \end{matrix}$ 的解是 .

查看试题解析

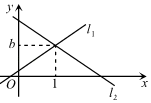
三、综合题

16. 如图， $l_{1}$ ， $l_{2}$ 分别表示两个一次函数的图象，它们相交于点P．

(1)、求出两条直线的函数关系式

(2)、点P的坐标可看作是哪个二元一次方程组的解．

查看试题解析
17. 习近平总书记说：“人民群众多读书，我们的民族精神就会厚重起来、深邃起来．”某书店计划在4月23日世界读书日之前，同时购进A，B两类图书，已知购进3本A类图书和4本B类图书共需288元；购进6本A类图书和2本B类图书共需306元．

(1)、A，B两类图书每本的进价各是多少元？

(2)、该书店计划用4500元全部购进两类图书，设购进A类x本，B类y本．
①求y关于x的关系式；

②进货时，A类图书的购进数量不少于60本，已知A类图书每本的售价为38元，B类图书每本的售价为50元，求如何进货才能使书店所获利润最大，最大利润为多少元？

查看试题解析
18. 如图，正比例函数 $y = - 3 x$ 的图象与一次函数 $y = k x + b$ 的图象交于点 $P (m ， 3)$ ，一次函数图象经过点 $B (1 ， 1)$ ，与y轴的交点为D，与x轴的交点为C.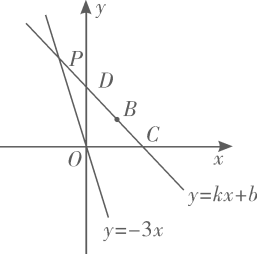

(1)、求一次函数表达式；

(2)、求D点的坐标；

(3)、求 $△ C O P$ 的面积.

(4)、不解关于x、y的方程组 ${\begin{matrix} y = - 3 x \\ y = k x + b \end{matrix}$ ，直接写出方程组的解.

查看试题解析
19. 定义：我们把一次函数 $y = k x + b (k \neq 0)$ 与正比例函数 $y = x$ 的交点称为一次函数 $y = k x + b (k \neq 0)$ 的“不动点”．例如求 $y = 2 x - 1$ 的“不动点”；联立方程 ${\begin{array}{l} y = 2 x - 1 \\ y = x \end{array}$ ，解得 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$ ，则 $y = 2 x - 1$ 的“不动点”为 $(1 ， 1)$ ．

(1)、由定义可知，一次函数 $y = 3 x + 2$ 的“不动点”为．

(2)、若一次函数 $y = m x + n$ 的“不动点”为 $(2 ， n - 1)$ ，求m、n的值．

(3)、若直线 $y = k x - 3 (k \neq 0)$ 与x轴交于点A，与y轴交于点B，且直线 $y = k x - 3$ 上没有“不动点”，若P点为x轴上一个动点，使得 $S_{△ A B P} = 3 S_{△ A B O}$ ，求满足条件的P点坐标．

查看试题解析

20. 一方有难，八方支援．“新冠肺炎”疫情来袭，除了医务人员主动请缨逆行走向战场外，众多企业也伸出援助之手，某公司用甲，乙两种货车向武汉运送爱心物资．两次满载的运输情况如表：

	甲种货车辆数	乙种货车辆数	合计运物资吨数
第一次	3	4	31
第二次	2	6	34

(1)、求甲、乙两种货车每次满载分别能运输多少吨物资；

(2)、由于疫情的持续，该公司安排甲乙货车共10辆进行第三次物资的运送，运送的物资不少于48.4吨，其中每辆甲车一次运送花费500元，每辆乙车一次运送花费300元，请问该公司应如何安排车辆最节省费用？

查看试题解析

x	…	﹣2	﹣1	0	1	2	…
y₁	…	﹣1	0	1	2	3	…
y₂	…	﹣5	﹣3	﹣1	1	3	…

2023-2024学年北师大版数学八年级上册 5.7用二元一次方程组确定一次函数表达式 同步练习（提升卷）

一、选择题

二、填空题

三、综合题

2023-2024学年北师大版数学八年级上册 5.7用二元一次方程组确定一次函数表达式同步练习（提升卷）