2023年浙教版数学七年级上册第五章 一元一次方程 单元测试(B卷)
试卷更新日期:2023-10-15 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 下列方程变形中,正确的是( )A、方程 , 移项得,; B、方程 , 去括号得,; C、方程 , 系数化为1得,; D、方程 , 去分母得, .2. 若不论 取什么实数,关于 的方程 ( 、 常数)的解总是 ,则 的值是( )A、 B、 C、 D、3. 若关于 x 的一元一次方程ax + 2x = 6 的解是正整数,则符合条件的所有整数 a 的和为( )A、0 B、4 C、12 D、204. 下列说法:
①符号相反的数互为相反数;②有理数a、b、c满足 ,且 ,则化简 的值为5;③若 是关于x的一元一次方程,则这个方程的解是 ;④若 是关于x的一元一次方程,则 ;
其中正确的有( )
A、4个 B、3个 C、2个 D、1个5. 求的值,可令 , 则 , 因此2S-S=22017-1,S=22017-1.参照以上推理,计算的值为( )A、42020-1 B、42020-4 C、 D、6. 小明在做解方程作业时,不小心将方程中的一个常数污染了看不清楚,被污染的方程是: , 怎么办呢?小明想了一想,便翻看书后答案,此方程的解是 , 于是很快就补好了这个常数,你能补出这个常数吗?它应是( ) A、4 B、3 C、2 D、17. 如图,现有3×3的方格,每个小方格内均有数字,要求方格内每一行.每一列以及每一条对角线上的三个数字之和均相等,记三个数字之和为P,则P的值是( )
, 怎么办呢?小明想了一想,便翻看书后答案,此方程的解是 , 于是很快就补好了这个常数,你能补出这个常数吗?它应是( ) A、4 B、3 C、2 D、17. 如图,现有3×3的方格,每个小方格内均有数字,要求方格内每一行.每一列以及每一条对角线上的三个数字之和均相等,记三个数字之和为P,则P的值是( )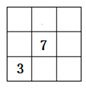 A、12 B、15 C、18 D、218. 《九章算术》中记载这样一道题:今有牛、马、羊食人苗.苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”大意是:现在有一头牛、一匹马、一只羊吃了别人家的禾苗,禾苗的主人要求这些动物的主人共计赔偿五斗粟米.羊的主人说:“我家羊只吃了马吃的禾苗的一半.”马的主人说:“我家马只吃了牛吃的禾苗的一半.”按此说法,羊的主人应当赔偿禾苗的主人多少斗粟米?( )A、 B、 C、 D、9. 如图是一块在电脑屏幕上出现的长方形色块图,由 6 个不同颜色的正方形组成,已知中间最小的一个正方形的边长为 1,那么这个长方形色块图的周长为( )
A、12 B、15 C、18 D、218. 《九章算术》中记载这样一道题:今有牛、马、羊食人苗.苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”大意是:现在有一头牛、一匹马、一只羊吃了别人家的禾苗,禾苗的主人要求这些动物的主人共计赔偿五斗粟米.羊的主人说:“我家羊只吃了马吃的禾苗的一半.”马的主人说:“我家马只吃了牛吃的禾苗的一半.”按此说法,羊的主人应当赔偿禾苗的主人多少斗粟米?( )A、 B、 C、 D、9. 如图是一块在电脑屏幕上出现的长方形色块图,由 6 个不同颜色的正方形组成,已知中间最小的一个正方形的边长为 1,那么这个长方形色块图的周长为( )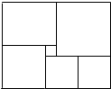 A、42 B、48 C、44 D、5010. 为响应习总书记“绿水青山,就是金山银山”的号召,某校今年3月争取到一批植树任务,领到一批树苗,按下列方法依次由各班领取:第一班领取全部的 , 第二班领取100棵和余下的 , 第三班领取200棵和余下的 , 第四班领取300棵和余下的……,最后树苗全部被领完,且各班领取的树苗数相等,则树苗总棵树为( )A、6400 B、8100 C、9000 D、4900
A、42 B、48 C、44 D、5010. 为响应习总书记“绿水青山,就是金山银山”的号召,某校今年3月争取到一批植树任务,领到一批树苗,按下列方法依次由各班领取:第一班领取全部的 , 第二班领取100棵和余下的 , 第三班领取200棵和余下的 , 第四班领取300棵和余下的……,最后树苗全部被领完,且各班领取的树苗数相等,则树苗总棵树为( )A、6400 B、8100 C、9000 D、4900二、填空题(每题3分,共18分)
-
11. 若关于 的方程 的解为整数,则非负整数 的值为.12. 已知等式:① ② ③ ④ ,其中可以通过适当变形得到 的等式是 . (填序号)13. 已知方程是关于x的一元一次方程,则该方程的解为 .14. 已知关于x的一元一次方程+5=2020x+m的解为x=2021,那么关于y的一元一次方程﹣5=2020(10﹣y)﹣m的解为 .15. 幻方历史悠久,传说最早出现在夏禹时代的“洛书”当中,根据幻方的相等关系设计出来一个“幻圆”,即大圆.小圆.横线.竖线上的四个数字加起来的和均相等.如图给出了部分数字,则幻圆中的值为 .
 16. 如图,商品条形码是商品的“身份证”,共有13位数字.它是由前12位数字和校验码构成,其结构分别代表“国家代码、厂商代码、产品代码、和校验码”.
16. 如图,商品条形码是商品的“身份证”,共有13位数字.它是由前12位数字和校验码构成,其结构分别代表“国家代码、厂商代码、产品代码、和校验码”.
其中,校验码是用来校验商品条形码中前12位数字代码的正确性.它的编制是按照特定的算法得来的.其算法为:
步骤1:计算前12位数字中偶数位数字的和 ,即 ;
步骤2:计算前12位数字中奇数位数字的和 ,即 ;
步骤3:计算 与 的和 ,即 ;
步骤4:取大于或等于 且为10的整数倍的最小数 ,即中 ;
步骤5:计算 与 的差就是校验码X,即 .
如图,若条形码中被污染的两个数字的和是5,则被污染的两个数字中右边的数字是.
三、解答题(共10题,共72分)
-
17. 解方程
(1)、(2)、(3)、18. 已知关于 的方程 为一元一次方程,且该方程的解与关于 的方程 的解相同.(1)、求 、 的值;(2)、在(1)的条件下,若关于 的方程 有无数解,求 , 的值.19. 将一个三位数分成4个数,使得第一个数乘以2,第二个数除以2,第三个数减1,第四个数加2,得到的结果相等,若该三位数比这四个数中最大的数的2倍大59,求这三位数.20. 定义:如果两个一元一次方程的解之和为1,我们就称这两个方程为“美好方程”.例如:方程和为“美好方程”.(1)、方程与方程是“美好方程”吗?请说明理由;(2)、若关于x的方程与方程是“美好方程”,求m的值;(3)、若关于x方程与是“美好方程”,求n的值.21. 某铁路由于沿线多为山壑,需修建桥梁和隧道共300个,桥梁和隧道的长度约占这条铁路全长的五分之四,其中桥梁数量座又比隧道数量条多50%这条铁路工程总投资约135亿元,平均每千米造价约4500万元.(1)、求该铁路隧道数量.(2)、若该铁路平均每条隧道长度大约是平均每座桥梁长度的6倍.求该铁路隧道的总长度.22. 科技馆在顺次有A,B,C三点的笔直跑道上,进行机器人行走性能试验.甲、乙两机器人分别从A,B两点按预定程序,同时同向出发,历时同时到达C点.乙机器人始终以的速度行走;甲机器人前匀速运动,在的这段时间,甲、乙两机器人的速度相同,在的这段时间,甲机器人再次匀速运动.甲、乙两机器人之间的距离与他们的行走时间之间的对应的不完整的数据记录如表.请结合表格,回答下列问题:0
1
2
3
4
5
6
7
60
0
y
y
0
(1)、A,B两点之间的距离是m,;(2)、求甲机器人前的速度;(3)、请直接写出在整个运动过程中,两机器人相距时t的值.23. 为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市民“一户一表“生活用水阶梯式计费价格表的部分信息:自来水销售价格
污水处理价格
每户每月用水量
单价:元吨
单价:元吨
17吨及以下
0.90
超过17吨但不超过30吨的部分
0.90
超过30吨的部分
6.00
0.90
说明:每户生产的污水量等于该户自来水用量;水费自来水费用污水处理费
已知小王家2018年7月用水16吨,交水费43.2元.8月份用水25吨,交水费75.5元.
(1)、求、的值;(2)、如果小王家9月份上交水费156.1元,则小王家这个月用水多少吨?(3)、小王家10月份忘记了去交水费,当他11月去交水费时发现两个月一共用水50吨,其中10月份用水超过30吨,一共交水费215.8元,其中包含30元滞纳金,求小王家11月份用水多少吨?滞纳金:因未能按期缴纳水费,逾期要缴纳的“罚款金额”24. 某校组织七年级师生到从化进行秋游活动,学校联系了快乐旅游公司提供车辆.该公司现有50座与35座两种车型.如果用35座的,会有5人没座位;如果全部换成50座,则可少用2辆车,而且多出15个座位.若35座客车日租金为每辆250元,50座客车日租金为每辆300元.(1)、该校七年级师生一共多少人参加了这次秋游活动?(2)、这次秋游活动一共有几种租车方案?哪一种方案最划算?(3)、从学校到目的地的路程为90千米,原计划3小时到达.在开了三分之一路程之后,堵车半小时.为了按时到达,请你帮司机算一下,车速应提高到每小时多少千米?25. 双十一临近,武汉掀起购物狂潮,现有甲,乙、丙三个商场开展的促销活动如下表所示:商场
优惠活动
甲
全场按标价的6折销售
乙
实行“每满100元送100元的购物券”的优惠,购物券可以在再购买时冲抵现金比如:顾客购衣服220元,赠券200元,再购买裤子时可冲抵现金,不再送券)
丙
实行“每满100元减50元的优惠”(比如,某顾客购物220元,他只需付款120元)
根据以上活动信息,解决以下问题:
(1)、三个商场同时出售一件标价290元的上衣和一条标价270元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场?(2)、黄先生发现在甲、乙商场同时出售一件标价380元的上衣和一条标价300多元的裤子,最后付款也一样,请问这条裤子的标价是多少元?(3)、丙商场又推出“先打折”,“再满100元减50元”的活动,张先生买了一件标价为630元的上衣,张先生发现竟然比没打折多付了18.5元钱,问丙商场先打了多少折后再参加活动(结果精确到0.01)26. 阅读理解:若、、为数轴上三点,若点到的距离是点到的距离倍,我们就称点是【 , 】的好点.
例如,如图 , 点表示的数为 , 点表示的数为表示的点到点的距离是 , 到点的距离是 , 那么点是【 , 】的好点;又如,表示的点到点的距离是 , 到点的距离是 , 那么点就不是【 , 】的好点,但点是【 , 】的好点.
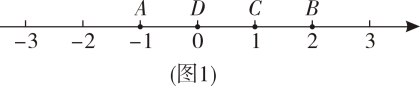
知识运用:如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为 .
 (1)、数所表示的点是【 , 】的好点;(2)、如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为现有一只电子蚂蚁从点出发,以个单位每秒的速度向左运动,到达点停止当为何值时,、和中恰有一个点为其余两点的好点?
(1)、数所表示的点是【 , 】的好点;(2)、如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为现有一只电子蚂蚁从点出发,以个单位每秒的速度向左运动,到达点停止当为何值时,、和中恰有一个点为其余两点的好点?