【浙教版】2023~2024学年八年级上册期中考试数学卷(一)
试卷更新日期:2023-10-13 类型:期中考试
一、选择题
-
1. 下列图标是节水、绿色食品、回收、节能的标志,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列长度的三条线段,首尾顺次相连能组成三角形的是( )A、 B、 C、 D、3. 若点 与点 关于 轴对称,则点 所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 某品牌自行车进价为每辆800元,标价为每辆1 200元.店庆期间,商场为了答谢顾客,进行打折促销活动,但是要保证利润率不低于 , 则最多可打( )折.A、六 B、七 C、八 D、九5. 根据下列已知条件,能画出惟一的△ABC的是( )A、AB=3cm,BC=7cm,AC=4cm B、AB=3cm,BC=7cm,∠C=40° C、∠A=30°,AB=3cm,∠B=100° D、∠A=30°,∠B=100°,∠C=50°6. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC,AB于点M,N,再分别以M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=4,AB=15,则△ABD的面积为( )
2. 下列长度的三条线段,首尾顺次相连能组成三角形的是( )A、 B、 C、 D、3. 若点 与点 关于 轴对称,则点 所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 某品牌自行车进价为每辆800元,标价为每辆1 200元.店庆期间,商场为了答谢顾客,进行打折促销活动,但是要保证利润率不低于 , 则最多可打( )折.A、六 B、七 C、八 D、九5. 根据下列已知条件,能画出惟一的△ABC的是( )A、AB=3cm,BC=7cm,AC=4cm B、AB=3cm,BC=7cm,∠C=40° C、∠A=30°,AB=3cm,∠B=100° D、∠A=30°,∠B=100°,∠C=50°6. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC,AB于点M,N,再分别以M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=4,AB=15,则△ABD的面积为( ) A、15 B、30 C、45 D、607. 下列命题:①全等三角形的对应角相等;②线段垂直平分线上的点到线段两端的距离相等;③等腰三角形的两个底角相等.其中逆命题是真命题的个数是( )A、0 B、1 C、2 D、38. 如图, , 平分 , 平分 , 且 , 下列结论:
A、15 B、30 C、45 D、607. 下列命题:①全等三角形的对应角相等;②线段垂直平分线上的点到线段两端的距离相等;③等腰三角形的两个底角相等.其中逆命题是真命题的个数是( )A、0 B、1 C、2 D、38. 如图, , 平分 , 平分 , 且 , 下列结论:平分;;; , 其中正确的有( )
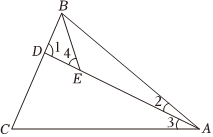
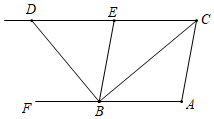 A、个 B、个 C、个 D、个9. 如图,在中,平分交AC于点D,且 , F在BC上,E为AF的中点,连接DE,若 , , , 则AB的长为( )
A、个 B、个 C、个 D、个9. 如图,在中,平分交AC于点D,且 , F在BC上,E为AF的中点,连接DE,若 , , , 则AB的长为( ) A、 B、 C、 D、910. 如图,在平面直角坐标系中,点A的坐标为(4,0),点Q是直线yx上的一个动点,以AQ为边,在AQ的右侧作等边△APQ,使得点P落在第一象限,连接OP,则OP+AP的最小值为( )
A、 B、 C、 D、910. 如图,在平面直角坐标系中,点A的坐标为(4,0),点Q是直线yx上的一个动点,以AQ为边,在AQ的右侧作等边△APQ,使得点P落在第一象限,连接OP,则OP+AP的最小值为( ) A、6 B、4 C、8 D、6
A、6 B、4 C、8 D、6二、填空题
-
11. 已知a,b,c是的三条边长,化简的结果为 .12. 如图,在中, , , , 平分则的度数为 .
 13. 如图,已知圆柱的底面直径为 , 高为5,一只小虫在圆柱表面爬行,从C点爬到A点,则这只小虫爬行的最短路程是 .
13. 如图,已知圆柱的底面直径为 , 高为5,一只小虫在圆柱表面爬行,从C点爬到A点,则这只小虫爬行的最短路程是 .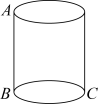 14. 如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E和点N在BC上,则∠EAN= .
14. 如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E和点N在BC上,则∠EAN= . 15. 关于x的不等式组只有4个整数解,则a的取值范围是 .16. 中,点D是斜边的中点.
15. 关于x的不等式组只有4个整数解,则a的取值范围是 .16. 中,点D是斜边的中点. (1)、如图1,若于E,于F, , , 则;(2)、如图2,若点P是的中点,且 , .
(1)、如图1,若于E,于F, , , 则;(2)、如图2,若点P是的中点,且 , .三、计算题
-
17. 解下列不等式组,并把解集在数轴上表示出来:(1)、(2)、
四、作图题
-
18. 如图,在3×6的方格纸中,已知格点P和线段AB.
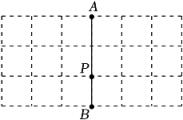
⑴画一个锐角三角形(顶点均在格点上且不与点A,B重合),使P为其中一边的中点.
⑵再画出该三角形关于直线AB对称的图形.
五、解答题
-
19. 已知:如图,点为线段上一点, , , . 求证: .
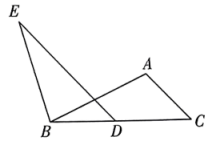 20. 如图,在中,是延长线上一点,满足 , 过点作 , 且 , 连接并延长,分别交 , 于点 , .(1)、求证:≌;(2)、若 , , 求的长度.
20. 如图,在中,是延长线上一点,满足 , 过点作 , 且 , 连接并延长,分别交 , 于点 , .(1)、求证:≌;(2)、若 , , 求的长度. 21. 某旅游景点的一个商场为了抓住国庆节长假这一旅游旺季的商机,决定购进甲,乙两种纪念品,若购进甲种纪念品1件、乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.(1)、购进甲乙两种纪念品每件各需要多少元?(2)、该商场决定购进甲乙两种纪念品共100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6000元,同时甲种纪念品又不能超过60件,则该商场共有几种进货方案?(3)、若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?22. 下面是小明同学证明定理时使用的两种添加辅助线的方法,选择其中一种,完成证明.
21. 某旅游景点的一个商场为了抓住国庆节长假这一旅游旺季的商机,决定购进甲,乙两种纪念品,若购进甲种纪念品1件、乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.(1)、购进甲乙两种纪念品每件各需要多少元?(2)、该商场决定购进甲乙两种纪念品共100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6000元,同时甲种纪念品又不能超过60件,则该商场共有几种进货方案?(3)、若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?22. 下面是小明同学证明定理时使用的两种添加辅助线的方法,选择其中一种,完成证明.定理:在直角三角形中,如果一个锐角等于 , 那么它所对的直角边等于斜边的一半.
已知:如图,在中, , .
求证: .
方法一
证明:如图,延长到点 , 使得 , 连接 .
方法二
证明:如图,在线段上取一点 , 使得 , 连接 . 23. 已知中, , 于点M,点D在直线上, , 垂足为点E, , 垂足为点F.
23. 已知中, , 于点M,点D在直线上, , 垂足为点E, , 垂足为点F.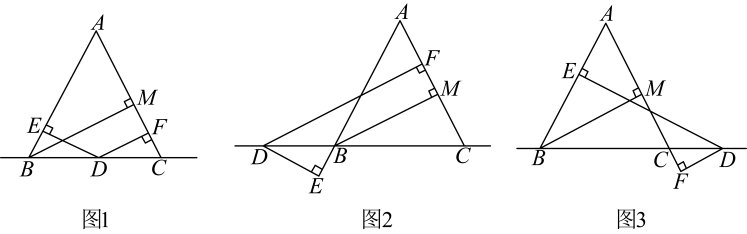 (1)、如图1,点D在边上时,小明同学利用①三角形全等知识和②图形等面积法两种方法发现了 , , 三线段之间的数量关系,请直接写出三线段之间的数量关系是;(2)、如图2,图3,当点D在点B左边或者在点C右边的直线上时,问题(1)中 , , 三线段的数量关系是否还成立?若成立请选择一个图形进行证明,若不成立,请在图2或图3中选择一个图形,写出三线段新的数量关系,并进行证明.24. 已知 .
(1)、如图1,点D在边上时,小明同学利用①三角形全等知识和②图形等面积法两种方法发现了 , , 三线段之间的数量关系,请直接写出三线段之间的数量关系是;(2)、如图2,图3,当点D在点B左边或者在点C右边的直线上时,问题(1)中 , , 三线段的数量关系是否还成立?若成立请选择一个图形进行证明,若不成立,请在图2或图3中选择一个图形,写出三线段新的数量关系,并进行证明.24. 已知 . (1)、如图1,按如下要求用尺规作图:
(1)、如图1,按如下要求用尺规作图:①作出的中线;
②延长至E,使 , 连接;(不要求写出作法,但要保留作图痕迹.)
(2)、如图2,若是中线.试探究与之间的数量关系,并说明理由;(3)、如图3,若是的中线,过点B作于E,交于点F,连接 . 若 , 求的长.
-
-