浙江省衢州市2023年中考数学试卷
试卷更新日期:2023-10-13 类型:中考真卷
一、选择题(本题共有10小题,每小题3分,共30分)
-
1. 手机信号的强弱通常采用负数来表示,绝对值越小表示信号越强(午位:),则下列信号最强的是( )A、-50 B、-60 C、-70 D、-802. 如图是国家级非物质文化遗产衢州莹白瓷的直口杯,它的主视图是( )
 A、
A、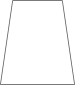 B、
B、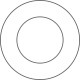 C、
C、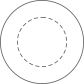 D、
D、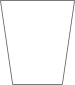 3. 下列运算,结果正确的是( )A、 B、 C、 D、4. 某公司5名员工在一次义务募捐中的捐款额为(单位:元):30,50,50,60,60.若捐款最少的员工又多捐了20元,则分析这5名员工捐款额的数据时,不受影响的统计量是( )A、平均数 B、中位数 C、众数 D、方差5. 下列各组数满足方程的是( )A、 B、 C、 D、6. 如图是脊柱侧弯的检测示意图,在体检时为方便测出Cobb角的大小,需将转化为与它相等的角,则图中与相等的角是( )
3. 下列运算,结果正确的是( )A、 B、 C、 D、4. 某公司5名员工在一次义务募捐中的捐款额为(单位:元):30,50,50,60,60.若捐款最少的员工又多捐了20元,则分析这5名员工捐款额的数据时,不受影响的统计量是( )A、平均数 B、中位数 C、众数 D、方差5. 下列各组数满足方程的是( )A、 B、 C、 D、6. 如图是脊柱侧弯的检测示意图,在体检时为方便测出Cobb角的大小,需将转化为与它相等的角,则图中与相等的角是( )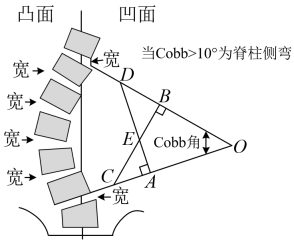 A、 B、 C、 D、7. 如图,在△ABC中,以点A为圆心,适当长为半径画弧,分别交AB,AC于点D,E.分别以点D,E为圆心,大于长为半径画弧,交于∠BAC内一点F.连结AF并延长,交BC于点G,连结DG,EG.添加下列条件,不能使BG=CG成立的是( )
A、 B、 C、 D、7. 如图,在△ABC中,以点A为圆心,适当长为半径画弧,分别交AB,AC于点D,E.分别以点D,E为圆心,大于长为半径画弧,交于∠BAC内一点F.连结AF并延长,交BC于点G,连结DG,EG.添加下列条件,不能使BG=CG成立的是( )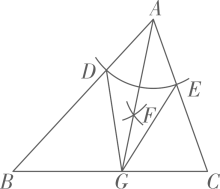 A、 B、 C、 D、8. 某人患了流感,经过两轮传染后共有36人患了流感.设每一轮传染中平均每人传染了人,则可得到方程( )A、 B、 C、 D、9. 如图,一款可调节的笔记本电脑支架放置在水平桌面上,调节杆的最大仰角为.当时,则点到桌面的最大高度是( )
A、 B、 C、 D、8. 某人患了流感,经过两轮传染后共有36人患了流感.设每一轮传染中平均每人传染了人,则可得到方程( )A、 B、 C、 D、9. 如图,一款可调节的笔记本电脑支架放置在水平桌面上,调节杆的最大仰角为.当时,则点到桌面的最大高度是( )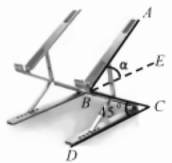 A、 B、 C、 D、10. 已知二次函数是常数,的图象上有和两点.若点A,B都在直线的上方,且 , 则的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 已知二次函数是常数,的图象上有和两点.若点A,B都在直线的上方,且 , 则的取值范围是( )A、 B、 C、 D、二、填空题(本题共有6小题,每小题4分,共24分)
-
11. 计算: .12. 衢州飞往成都每天有2趟航班.小赵和小黄同一天从衢州飞往成都,如果他们可以选择其中任一航班,则他们选择同一航班的概率等于.13. 在如图所示的方格纸上建立适当的平面直角坐标系,若点的坐标为 , 点的坐标为 , 则点的坐标为.
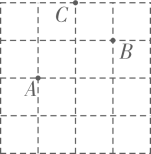 14. 如图是一个圆形餐盘的正面及其固定支架的截面图,凹槽ABCD是矩形.当䝳盘正立且紧靠支架于点A,D时,恰好与BC边相切,则此餐盘的半径等于.
14. 如图是一个圆形餐盘的正面及其固定支架的截面图,凹槽ABCD是矩形.当䝳盘正立且紧靠支架于点A,D时,恰好与BC边相切,则此餐盘的半径等于.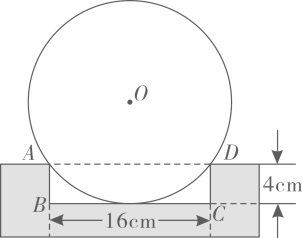 15. 如图,点A,B在轴上,分别以OA,AB为边,在轴上方作正方形OACD,ABEF.反比例函数的图象分别交边CD,BE于点P,Q.作轴于点轴于点.若为BE的中点,且阴影部分面积等于6,则的值为.
15. 如图,点A,B在轴上,分别以OA,AB为边,在轴上方作正方形OACD,ABEF.反比例函数的图象分别交边CD,BE于点P,Q.作轴于点轴于点.若为BE的中点,且阴影部分面积等于6,则的值为.
 16. 下面是勾股定理的一种证明方法:图1所示纸片中, , 四边形ACDE,CBFG是正方形.过点C,B将纸片CBFG分别沿与AB平行、垂直两个方向剪裁成四部分,并与正方形拼成图2.
16. 下面是勾股定理的一种证明方法:图1所示纸片中, , 四边形ACDE,CBFG是正方形.过点C,B将纸片CBFG分别沿与AB平行、垂直两个方向剪裁成四部分,并与正方形拼成图2. (1)、若的面积为16,则纸片Ⅲ的面积为.(2)、若 , 则.
(1)、若的面积为16,则纸片Ⅲ的面积为.(2)、若 , 则.三、解答题(本题共有8小题,第 rId164 小题每小题6分,第 rId166 小题每小题8分,第 rId168 23小题每小题10分,第24小题12分,共66分.请务必写出解答过程
-
17.(1)、计算:.(2)、化简:.18. 小红在解方程时,第一步出现了错误:
 (1)、请在相应的方框内用横线划出小红的错误处.(2)、写出你的解答过程.19. 已知:如图,在和中,在同一条直线上.下面四个条件:
(1)、请在相应的方框内用横线划出小红的错误处.(2)、写出你的解答过程.19. 已知:如图,在和中,在同一条直线上.下面四个条件:①②;③;④
 (1)、请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可).(2)、在(1)的条件下,求证:△ABC≌△DEF.20. 【数据的收集与整理】
(1)、请选择其中的三个条件,使得△ABC≌△DEF(写出一种情况即可).(2)、在(1)的条件下,求证:△ABC≌△DEF.20. 【数据的收集与整理】根据国家统计局统一部署﹐衢州市统计局对2022年我市人口变动情况进行了抽样调查,抽样比例为5‰.根据抽样结果推算,我市2022年的出生率为5.5‰,死亡率为8‰,人口自然增长率为-2.5‰,常住人口数为人(‰来示千分号).
(数据来源:衢州市统计局)【数据分析】
(1)、请根据信息推测人口自然增长率与出生率、死亡率的关系.(2)、已知本次调查的样本容量为11450,请推算的值.(3)、将我市及全国近五年的人口自然增长率情况绘制成如下统计图.根据统计图分析:
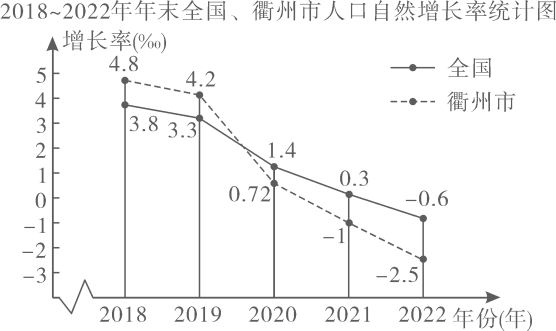
①对图中信息作出评判(写出两条).
②为扭转目前人口自然增长率的趋势,请给出一条合理化建议.
21. 如图,在Rt中,为AC边上一点,连结OB.以OC为半径的半圆与AB边相切于点 , 交AC边于点.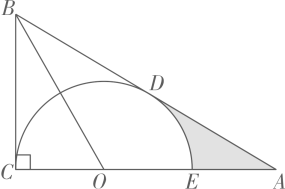 (1)、求证:.(2)、若.
(1)、求证:.(2)、若.①求半圆的半径.
②求图中阴影部分的面积.
22. 视力表中蕴含着很多数学知识,如:每个“ ”形图都是正方形结构,同一行的“
”形图都是正方形结构,同一行的“ ”是全等图形且对应着同一个视力值,不同的检测距离需要不同的视力表.
”是全等图形且对应着同一个视力值,不同的检测距离需要不同的视力表. 素材1国际通用的视力表以5米为检测距离,任选视力表中7个视力值 , 测得对应行的“
 ”形图边长 , 在平面直角坐标系中描点如图1.
”形图边长 , 在平面直角坐标系中描点如图1.探究1检测距离为5米时,归纳与的关系式,并求视力值1.2所对应行的“
 ”形图边长.
”形图边长.
素材2图2为视网膜成像示意图,在检测视力时,眼晴能看清最小“
 ”形图所成的角叫做分辨视角.视力值与分辨视角(分)的对应关系近似满足).
”形图所成的角叫做分辨视角.视力值与分辨视角(分)的对应关系近似满足).探究2当时,属于正常视力,根据函数增减性写出对应的分辦视角的范围.
素材3如图3,当确定时,在处用边长为的号“
 ”测得的视力与在处用边长为的Ⅱ号“
”测得的视力与在处用边长为的Ⅱ号“ ”测得的视力相同.
”测得的视力相同.探究3若检测距离为3米,求视力值1.2所对应行的“
 ”形图边长.23. 某龙舟队进行500米直道训练,全程分为启航,途中和冲刺三个阶段.图1,图2分别表示启航阶段和途中阶段龙舟划行总路程与时间的近似函数图象.启航阶段的函数表达式为;途中阶段匀速划行,函数图象为线段;在冲刺阶段,龙舟先加速后匀速划行,加速期龙舟划行总路程与时间的函数表达式为.
”形图边长.23. 某龙舟队进行500米直道训练,全程分为启航,途中和冲刺三个阶段.图1,图2分别表示启航阶段和途中阶段龙舟划行总路程与时间的近似函数图象.启航阶段的函数表达式为;途中阶段匀速划行,函数图象为线段;在冲刺阶段,龙舟先加速后匀速划行,加速期龙舟划行总路程与时间的函数表达式为.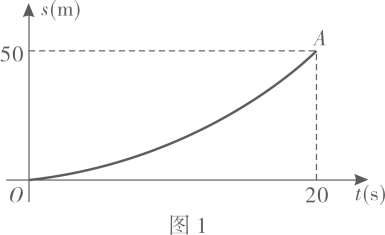
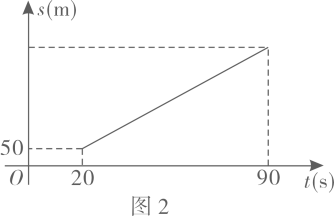 (1)、求出启航阶段关于的函数表达式(写出自变量的取值范围).(2)、已知途中阶段龙舟速度为.
(1)、求出启航阶段关于的函数表达式(写出自变量的取值范围).(2)、已知途中阶段龙舟速度为.①当时,求出此时龙舟划行的总路程.
②在距离终点125米处设置计时点,龙舟到达时,视为达标.请说明该龙舟队能否达标.
(3)、冲刺阶段,加速期龙舟用时将速度从提高到 , 之后保持匀速划行至终点.求该龙舟以完成训练所需时间(精确到).24. 如图1,点为矩形ABCD的对称中心, , 点为AD边上一点 , 连结EO并延长,交BC于点.四边形ABFE与关于EF所在直线成轴对称,线段交AD边于点。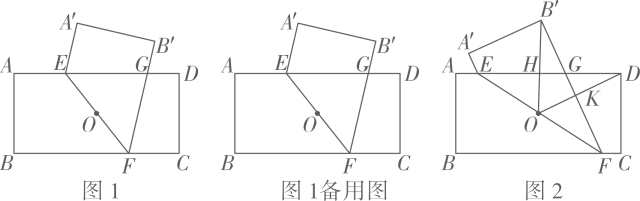 (1)、求证:.(2)、当时,求AE的长.(3)、令AE=a,DG=b.
(1)、求证:.(2)、当时,求AE的长.(3)、令AE=a,DG=b.①求证:(4-a)(4-b)=4.
②如图2,连结 , 分别交于点H,K.记四边形OKGH的面积为 , 的面积为.当时,求的值.