(单元测试B卷)第七章 平行线的证明—北师大版2023-2024学年八年级数学上册
试卷更新日期:2023-10-12 类型:单元试卷
一、选择题
-
1. 如图,直线 , 点在直线上,点、在直线上,且 , 平分 , 若 , 则的度数是( )
 A、 B、 C、 D、2. 如图,线段AB、CD相交于点O , 连接AD、CB , 和∠BCD的平分线AP和CP相交于点P , 则∠P与∠D、∠B之间存在的数量关系为( )
A、 B、 C、 D、2. 如图,线段AB、CD相交于点O , 连接AD、CB , 和∠BCD的平分线AP和CP相交于点P , 则∠P与∠D、∠B之间存在的数量关系为( ) A、 B、 C、 D、3. 下列说法正确的个数是( )
A、 B、 C、 D、3. 下列说法正确的个数是( )①函数的图象不经过第三象限
②一组数据5,6,7,6,8,10的众数和中位数都是6
③将的图象沿y轴向下平移3个单位长度后,图象经过原点
④式子有意义的条件是且
A、1 B、2 C、3 D、44. 如图,一束平行太阳光照射到正六边形上,若 , 则的大小为( ) A、150° B、148° C、140° D、138°5. 下列命题中,假命题是( )A、全等三角形对应角相等 B、对顶角相等 C、同位角相等 D、有两边对应相等的直角三角形全等6. 如图, , 下列推理正确的是( )
A、150° B、148° C、140° D、138°5. 下列命题中,假命题是( )A、全等三角形对应角相等 B、对顶角相等 C、同位角相等 D、有两边对应相等的直角三角形全等6. 如图, , 下列推理正确的是( )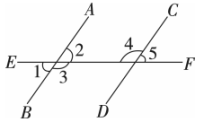
①若 , 则;②若 , 则;③若 , 则;④若 , 则.
A、①② B、②④ C、②③④ D、②③7. 如图,在中, , , , 则射线 与 ( ) A、平行 B、延长后相交 C、反向延长后相交 D、可能平行也可能相交8. 如图, , , 平分 , 平分 , 则( )
A、平行 B、延长后相交 C、反向延长后相交 D、可能平行也可能相交8. 如图, , , 平分 , 平分 , 则( )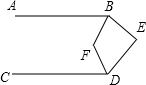 A、 B、 C、 D、9. 如图,直线 , 点E、F分别是AB、CD上的点(点E在点F的右侧),点M为线段EF上的一点(点M不与点E、F重合),点N为射线FD上的一动点,连接MN,过点M作 , 且恰能使得MQ平分∠EMN.若 , 则∠MNF和∠FMN的度数分别为( )
A、 B、 C、 D、9. 如图,直线 , 点E、F分别是AB、CD上的点(点E在点F的右侧),点M为线段EF上的一点(点M不与点E、F重合),点N为射线FD上的一动点,连接MN,过点M作 , 且恰能使得MQ平分∠EMN.若 , 则∠MNF和∠FMN的度数分别为( ) A、38°,76° B、38°,104° C、36°,142° D、36°,104°10. 下列各图中,当a∥b时,符合∠1=∠2+∠3关系的是( )A、
A、38°,76° B、38°,104° C、36°,142° D、36°,104°10. 下列各图中,当a∥b时,符合∠1=∠2+∠3关系的是( )A、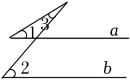 B、
B、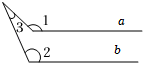 C、
C、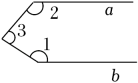 D、
D、
二、填空题
-
11. 把命题“锐角小于它的补角”改写成“如果那么”的形式为 .12. 如图,四边形ABCD中,∠A=100°,点M、N分别在AB、BC上,将△BMN沿MN翻折,FN∥DC , 则∠B的度数为°.
 13. 下列命题:①若|a|=-a,则a<0;②内错角相等;③平行于同一条直线的两条直线平行;④直线a、b、c在同一平面内,若a⊥b,a⊥c,则bc;⑤实数包括有理数和无理数.其中正确的命题序号有 .14. 如图,在△ABC和△ADE中,∠BAC =∠DAE=90°,∠B=50°,∠E=65°,则①∠1=∠3;②∠CAD+∠2=180°;③如果∠2=40°,则有BC∥AD;④如果∠2=30°,则有AC∥DE,上述结论中正确的是 .(填写序号)
13. 下列命题:①若|a|=-a,则a<0;②内错角相等;③平行于同一条直线的两条直线平行;④直线a、b、c在同一平面内,若a⊥b,a⊥c,则bc;⑤实数包括有理数和无理数.其中正确的命题序号有 .14. 如图,在△ABC和△ADE中,∠BAC =∠DAE=90°,∠B=50°,∠E=65°,则①∠1=∠3;②∠CAD+∠2=180°;③如果∠2=40°,则有BC∥AD;④如果∠2=30°,则有AC∥DE,上述结论中正确的是 .(填写序号)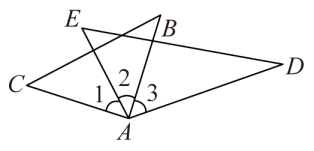 15. 如图,已知三内角的角平分线交于点D,三边的垂直平分线交于点E,若 , 则度.
15. 如图,已知三内角的角平分线交于点D,三边的垂直平分线交于点E,若 , 则度.
三、综合题
-
16. 如图,点B在CD上,OB=OD , AB=CD , ∠OBA=∠D;
 (1)、求证:△ABO≌△CDO;(2)、当AO∥CD , ∠BOD=30°,求∠A的度数.17. 将一副三角板中的两块直角三角板如图放置, , , , , .
(1)、求证:△ABO≌△CDO;(2)、当AO∥CD , ∠BOD=30°,求∠A的度数.17. 将一副三角板中的两块直角三角板如图放置, , , , , . (1)、若三角板如图摆放时,则 , .(2)、现固定的位置不变,将沿方向平移至点正好落在上,如图所示,与交于点 , 作和的角平分线交于点 , 求的度数;(3)、现固定 , 将绕点顺时针旋转至与直线首次重合的过程中,当线段与的一条边平行时,请直接写出的度数.18. 探究问题:已知∠ABC , 画一个角∠DEF , 使DE∥AB , EF∥BC , 且DE交BC于点P . ∠ABC与∠DEF有怎样的数量关系?
(1)、若三角板如图摆放时,则 , .(2)、现固定的位置不变,将沿方向平移至点正好落在上,如图所示,与交于点 , 作和的角平分线交于点 , 求的度数;(3)、现固定 , 将绕点顺时针旋转至与直线首次重合的过程中,当线段与的一条边平行时,请直接写出的度数.18. 探究问题:已知∠ABC , 画一个角∠DEF , 使DE∥AB , EF∥BC , 且DE交BC于点P . ∠ABC与∠DEF有怎样的数量关系? (1)、我们发现∠ABC与∠DEF有两种位置关系:如图1与图2所示.
(1)、我们发现∠ABC与∠DEF有两种位置关系:如图1与图2所示.①图1中∠ABC与∠DEF数量关系为;图2中∠ABC与∠DEF数量关系为;
请选择其中一种情况说明理由.
②由①得出一个真命题(用文字叙述): .
(2)、应用②中的真命题,解决以下问题:若两个角的两边互相平行,且一个角比另一个角的2倍少30°,请直接写出这两个角的度数.
19. 问题情境在综合与实践课上,同学们以“一个含的直角三角尺和两条平行线”为背景开展数学活动如图1,已知两直线a,b且和直角三角形 , , , .
 (1)、在图1中, , 求的度数;(2)、如图2,创新小组的同学把直线a向上平移,并把的位置改变,发现是一个定值,请写出这个定值,并说明理由;
(1)、在图1中, , 求的度数;(2)、如图2,创新小组的同学把直线a向上平移,并把的位置改变,发现是一个定值,请写出这个定值,并说明理由; (3)、缜密小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,平分 , 此时发现与又存在新的数量关系,请直接写出与的数量关系.
(3)、缜密小组在创新小组发现结论的基础上,将图2中的图形继续变化得到图3,平分 , 此时发现与又存在新的数量关系,请直接写出与的数量关系. 20. 如图
20. 如图
 (1)、在图1中,请直接写出、、、之间的数量关系:;(2)、仔细观察,在图2中“8字形”的个数 个;(3)、如果图2中, , , 与分别是和的角平分线,试求的度数;(4)、如果图2中和为任意角,其他条件不变,试问与 , 之间存在着怎样的数量关系(直接写出结论即可).21. 问题情景:如图1,在同一平面内,点B和点C分别位于一块直角三角板 的两条直角边 , 上,点A与点P在直线 的同侧,若点P在 内部,试问 , 与 的大小是否满足某种确定的数量关系?
(1)、在图1中,请直接写出、、、之间的数量关系:;(2)、仔细观察,在图2中“8字形”的个数 个;(3)、如果图2中, , , 与分别是和的角平分线,试求的度数;(4)、如果图2中和为任意角,其他条件不变,试问与 , 之间存在着怎样的数量关系(直接写出结论即可).21. 问题情景:如图1,在同一平面内,点B和点C分别位于一块直角三角板 的两条直角边 , 上,点A与点P在直线 的同侧,若点P在 内部,试问 , 与 的大小是否满足某种确定的数量关系?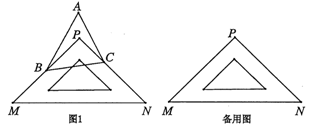 (1)、特殊探究:若 ,则 度, 度, 度;(2)、类比探索:请猜想 与 的关系,并说明理由;(3)、类比延伸:改变点A的位置,使点P在 外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出 , 与 满足的数量关系式.22. 问题情境:如图1,已知
(1)、特殊探究:若 ,则 度, 度, 度;(2)、类比探索:请猜想 与 的关系,并说明理由;(3)、类比延伸:改变点A的位置,使点P在 外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出 , 与 满足的数量关系式.22. 问题情境:如图1,已知 ,
, 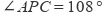 .求
.求  的度数.
的度数. (1)、经过思考,小敏的思路是:如图2,过P作
(1)、经过思考,小敏的思路是:如图2,过P作 ,根据平行线有关性质,可得
,根据平行线有关性质,可得 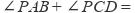 . (2)、问题迁移:如图3,
. (2)、问题迁移:如图3, ,点P在射线OM上运动,
,点P在射线OM上运动,  ,
, 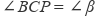 .
. ①当点P在A,B两点之间运动时,
 、
、  、
、  之间有何数量关系?请说明理由.
之间有何数量关系?请说明理由.②如果点P在A,B两点外侧运动时(点P与点A,B,O三点不重合),请你直接写出
 、
、  、
、  之间的数量关系,(3)、问题拓展:如图4,
之间的数量关系,(3)、问题拓展:如图4, ,
,  是一条折线段,依据此图所含信息,把你所发现的结论,用简洁的数学式子表达为.
是一条折线段,依据此图所含信息,把你所发现的结论,用简洁的数学式子表达为.