(单元测试A卷)第七章 平行线的证明—北师大版2023-2024学年八年级数学上册
试卷更新日期:2023-10-12 类型:单元试卷
一、选择题
-
1. 已知△ABC的三边分别是a、b、c,下列条件中不能判断△ABC为直角三角形的是( )A、a2+b2=c2 B、∠A:∠B:∠C=3:4:5 C、∠A=∠C-∠B D、a=1,b=2,c=2. 如图:①②③中,∠A=42°,∠1=∠2,∠3=∠4,则( )度.
 A、84 B、111 C、225 D、2013. 如图, , 点在直线上,且 , , 那么( )
A、84 B、111 C、225 D、2013. 如图, , 点在直线上,且 , , 那么( ) A、 B、 C、 D、4. 下列命题是假命题的是( )A、是最简二次根式 B、若点在直线 , 则 C、三角形的外角一定大于它的内角 D、同旁内角互补,两直线平行5. 如图,直线 , 一直角三角板ABC(∠ACB=90° )放在平行线上,两直角边分别l1与l2、交于点D、E,现测得∠1=75° , 则∠2的度数为( )
A、 B、 C、 D、4. 下列命题是假命题的是( )A、是最简二次根式 B、若点在直线 , 则 C、三角形的外角一定大于它的内角 D、同旁内角互补,两直线平行5. 如图,直线 , 一直角三角板ABC(∠ACB=90° )放在平行线上,两直角边分别l1与l2、交于点D、E,现测得∠1=75° , 则∠2的度数为( ) A、15° B、25° C、30° D、35°6. 如图,下列条件中,一定能判断的是( )
A、15° B、25° C、30° D、35°6. 如图,下列条件中,一定能判断的是( )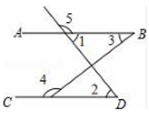 A、 B、 C、 D、7. 如图,直线a∥b,直角三角板ABC的直角顶点C在直线b上,若∠1=55°,则∠2=( )
A、 B、 C、 D、7. 如图,直线a∥b,直角三角板ABC的直角顶点C在直线b上,若∠1=55°,则∠2=( )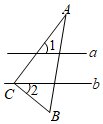 A、55° B、45° C、35° D、25°8. 下列说法正确的是( )A、过直线上一点有且只有一条直线与已知直线平行 B、不相交的两条直线叫做平行线 C、直线外一点到该直线的所有线段中垂线最短 D、过直线外一点有且只有一条直线与已知直线平行9. 下列图形中,由∠1=∠2,能得到AB∥CD的是( ).A、
A、55° B、45° C、35° D、25°8. 下列说法正确的是( )A、过直线上一点有且只有一条直线与已知直线平行 B、不相交的两条直线叫做平行线 C、直线外一点到该直线的所有线段中垂线最短 D、过直线外一点有且只有一条直线与已知直线平行9. 下列图形中,由∠1=∠2,能得到AB∥CD的是( ).A、 B、
B、 C、
C、 D、
D、 10. 如图,图中给出了过直线外一点作已知直线的平行线的方法,其依据的是( )
10. 如图,图中给出了过直线外一点作已知直线的平行线的方法,其依据的是( ) A、同位角相等,两直线平行 B、同旁内角互补,两直线平行 C、内错角相等,两直线平行 D、同平行于一条直线的两直线平行
A、同位角相等,两直线平行 B、同旁内角互补,两直线平行 C、内错角相等,两直线平行 D、同平行于一条直线的两直线平行二、填空题
-
11. 如图,已知 , , , 则 .
 12. 已知:直线 , 将一块含角的直角三角板如图所示放置,若 , 则度.
12. 已知:直线 , 将一块含角的直角三角板如图所示放置,若 , 则度. 13. 将命题“线段垂直平分线上的点到线段两端的距离相等”改写成“如果……,那么……”的形式为 .14. “过点P作直线b,使b∥a",小明的作图痕迹如图所示,他的作法的依据是
13. 将命题“线段垂直平分线上的点到线段两端的距离相等”改写成“如果……,那么……”的形式为 .14. “过点P作直线b,使b∥a",小明的作图痕迹如图所示,他的作法的依据是 15. 某同学按照某种规律写了下面一串数字:122122122122122…,当写完第93个数字时,1出现的频数是 .
15. 某同学按照某种规律写了下面一串数字:122122122122122…,当写完第93个数字时,1出现的频数是 .三、解答题
-
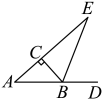
16. 如图,在中, , , 的外角的平分线交的延长线于点E.求的度数.
 17. 如图,已知: , , . 求证: .
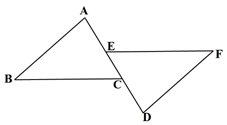
17. 如图,已知: , , . 求证: . 18. 点E、C在线段AD上, AB//DF, AE = DC, CB∥FE
18. 点E、C在线段AD上, AB//DF, AE = DC, CB∥FE求证: △ABC ≌ △DFE
 19. 下列各命题的条件是什么?结论是什么?(1)、两直线平行,同位角相等;(2)、过一点有且只有一条直线与已知直线平行.
19. 下列各命题的条件是什么?结论是什么?(1)、两直线平行,同位角相等;(2)、过一点有且只有一条直线与已知直线平行.四、综合题



