（单元测试A卷）第六章 数据的分析—北师大版2023-2024学年八年级数学上册

试卷更新日期：2023-10-12 类型：单元试卷

进入 出卷网 下载

一、选择题（每题3分，共30分）

  • 1. 某次数学测验中，八（1）班55人平均分为80分，八（2）班45人平均分为70分，则这两个班总平均分为（    ）
    A、75分 B、75.5分 C、76分 D、76.5分

    查看试题解析

  • 2. 小雨同学参加了学校举办的“抗击疫情，你我同行”主题演讲比赛，她的演讲内容语言表达和形象风度三项得分分别为80分，90分，85分，若这三项依次按照50%，30%，20%的百分比确定成绩，则她的成绩是（   ）
    A、82分 B、83分 C、84分 D、85分

    查看试题解析

  • 3. 某校男子篮球队10名队员进行定点投篮练习，每人投篮10次，将他们投中的次数进行统计制成下表：则这10名队员投中的次数组成的一组数据中，众数和中位数分别为（    ）

    投中次数

    3

    5

    6

    7

    8

    9

    人数

    1

    3

    2

    2

    1

    1

    A、5，6 B、2，6 C、5，5 D、6，5

    查看试题解析

  • 4. 欣欣商店在一段时间内销售了四种饮料共100瓶，各品牌饮料的销售量如表，根据表中数据，建议该商店进货数量最多的品牌是（ ）

    品牌

    甲

    乙

    丙

    丁

    销售量（瓶）

    15

    30

    12

    43
    A、甲品牌 B、乙品牌 C、丙品牌 D、丁品牌

    查看试题解析

  • 5. 若一组数据x ， 1 ， 4的中位数为3，则x的值为（ ）
    A、1 B、2 C、3 D、4

    查看试题解析

  • 6. 某次射击比赛，甲队员的成绩如图，根据此统计图，下列结论中错误的是（    ）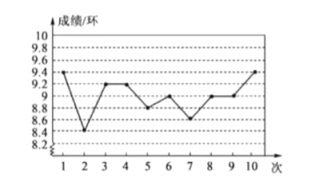

    A、最高成绩是9.4环 B、平均成绩是9环 C、这组成绩的众数是9环 D、这组成绩的方差是8.7

    查看试题解析

  • 7. 快要到新年了，某鞋店老板要进一批新年鞋，他一定会参考下面的调查数据，他最关注的是（　　）
    A、中位数 B、平均数 C、加权平均数 D、众数

    查看试题解析

  • 8. 如图所示是根据某地某月10天的每天最高气温绘成的折线统计图，那么这段时间该地最高气温的平均数、众数、中位数依次是（    ）

    A、4，5，4 B、4.5，5，4.5 C、4，5，4.5 D、4.5，5，4

    查看试题解析

  • 9. 某班准备从甲、乙、丙、丁四名同学中选一名最优秀的参加禁毒知识比赛，下表记录了四人3次选拔测试的相关数据：

    甲

    乙

    丙

    丁

    平均分

    95

    93

    95

    94

    方差

    3.2

    3.2

    4.8

    5.2

    根据表中数据，应该选择（   ）

    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 10. 学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛，各组的平时成绩的平均数（单位：分）及方差如表所示：


    甲

    乙

    丙

    丁

    平均数

    7

    8

    8

    7

    方差

    l

    1.5

    1

    1.8

    如果要选出一个成绩较好且状态稳定的小组去参赛，那么应选的小组是（    ）

    A、甲 B、乙 C、丙 D、丁

    查看试题解析

二、填空题（每题3分，共15分）

  • 11. 某校规定学生的数学学期综合成绩由平时、期中和期末三项成绩按3：3：4的比例计算所得.若小航同学本学期数学的平时、期中和期末成绩分别是80分、85分和90分，则他本学期数学学期以合成绩是分.

    查看试题解析

  • 12. 体育课中7名同学的“一分钟跳绳”的成绩如表(单位：个/分)：                                                                                                                                                      

    姓名

    李明

    王红

    刘丽

    王佳

    张强

    赵桐

    周馨

    成绩

             178

             183

             180

             181

             183

             183

             178

    则这组数据的中位数是 ．

    查看试题解析

  • 13. 已知一组数据2，2，x，3，3，4若众数是2，则中位数是.

    查看试题解析

  • 14. 学校运动会上，共有15名同学参加了男子100米预赛，参赛选手要想知道自己是否能进入前8名，从而取得决赛资格，只需要了解自己的成绩以及全部成绩的 ．

    查看试题解析

  • 15. 现有两组数据：甲：12，14，16，18；乙：2023，2022，2020，2019，它们的方差分别记作S甲2 ， S乙2 ， 则S甲2S乙2（用“>”“=”“<”）.

    查看试题解析

三、解答题（共4题，共20分）

  • 16. 某学校评选先进班集体，从“学习”、“卫生”、纪律”、活动参与”四个方面考核打分，各项满分均为100分，按比例计算综合得分，各项所占比例如表所示：
    项目 学习 卫生 纪律 活动参与
    所占比例 40% 25% 25% 10%

    八年级（1）班这四项得分依次为95分，90分，88分，80分，若学校规定班级四项综合得分超过90分的将会获得先进班集体，请你通过计算说明该班是否会获得先进班集体？

    查看试题解析

  • 17. 某校八年级（1）班一个小组十位同学的年龄（岁）分别如下；13,13,14,14,14,14,15,15,16,17;求这十位同学年龄的平均数、中位数、众数。

    查看试题解析

  • 18.

    柴静自费力作《穹顶之下》关于雾霾的深度调查中，提到2014雾霾天超过200天的城市，让人难以想象的是杭州竟然位列其中．据调查造成杭州雾霾严重的主要原因是汽车尾气的排放，它占到PM2.5来源的40%，下面是近几年杭州汽车保有量的统计图，请指出：

    （1）哪一年汽车增长的速度最快．

    （2）请计算2013年汽车的年增长率，2014年杭州限牌后增长速度有所缓解，如果没有限牌，继续按着03年的增长率继续增长（以后每年的增长率相同）预计2014年汽车保有量达到多少，2016年呢？（精确到个位）

    （3）请对改善杭州的环境提出一个有效的建议．

     

    查看试题解析

  • 19. 甲、乙两人在 5 次打靶测试中命中的环数如下：

    第一次

    第二次

    第三次

    第四次

    第五次

    甲

    8

    8

    7

    8

    9

    乙

    6

    9

    7

    9

    9

    从数据来看，谁的成绩较稳定？请你通过计算方差说明理由.

    查看试题解析

四、综合题（共4题，共35分）

  • 20. 某校为了提升初中学生学习数学的兴趣，举办“玩转数学”比赛．现有甲、乙两个小组进入决赛，评委从准备工作、研究报告、小组展示、答辩四个方面为各小组打分，各项成绩均按百分制记录，甲、乙两个小组各项得分如下表：

    小组

    准备工作

    研究报告

    小组展示

    答辩

    甲

    85

    78

    85

    73

    乙

    73

    80

    82

    83

    (1)、计算各小组的平均成绩，哪个小组的成绩高？
    (2)、如果按2：1：3：4的比来计算，求各小组的成绩，哪个小组的成绩高？

    查看试题解析

  • 21. 本学期初，某校为迎接中华人民共和国成立七十周年，开展了以“不忘初心，缅怀革命先烈，奋斗新时代“为主题的读书活动．德育处对八年级学生九月份“阅读该主题相关书籍的读书量”（ 下面简称：“读书量”）进行了随机抽样调查，并对所有随机抽取学生的“读书量”（单位：本）进行了统计，绘制了两幅不完整的统计图（如图所示）．

    (1)、请补全两幅统计图；本次所抽取学生九月份“读书量“的众数是多少；
    (2)、求本次所抽取学生九月份“读书量”的平均数；
    (3)、已知该校八年级有500名学生，请你估计该校八年级学生中，九月份“读书量“为5本的学生人数．

    查看试题解析

  • 22. 为振兴乡村经济，在农产品网络销售中实行目标管理，根据目标完成的情况对销售员给予适当的奖励，某村委会统计了15名销售员在某月的销售额（单位：万元），数据如下：10，4，7，5，4，10，5，4，4，18，8，3，5，10，8.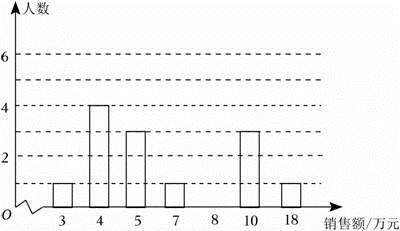

    (1)、补全月销售额数据的条形统计图；
    (2)、月销售额在哪个值的人数最多（众数）？中间的月销售额（中位数）是多少？平均月销售额（平均数）是多少？

    查看试题解析

  • 23. 某校举办国学知识竞赛，设定满分10分，学生得分均为整数.在初赛中，甲、乙两组（每组10人）学生成绩如下（单位：分）

    甲组：5，6，6，6，6，6，7，9，9，10.

    乙组：5，6，6，6，7，7，7，7，9，10.

    组别

    平均数

    中位数

    众数

    方差

    甲组

    7

    a

    6

    2.6

    乙组

    b

    7

    c

    S乙2

    (1)、以上成绩统计分析表中a= ， b= ， c=；
    (2)、小明同学说：“这次竞赛我得了7分，在我们小组中属中游略偏上!”观察上面表格判断，小明可能是组的学生；
    (3)、从平均数和方差看，若从甲、乙两组学生中选择一个成绩较为稳定的小组参加决赛，应选哪个组？并说明理由.

    查看试题解析