(北师大版)2023-2024学年八年级数学上册7.4 平行线的性质 同步测试
试卷更新日期:2023-10-12 类型:同步测试
一、选择题
-
1. 如图,直线EF∥MN,将一块含45°角的直角三角板(∠C=90°)如图摆放,∠CQM=66°,则∠AHE的度数是( )
 A、120° B、118° C、115° D、111°2. 如图,已知 , , 那么添加下列一个条件后,能判定≌的是( )
A、120° B、118° C、115° D、111°2. 如图,已知 , , 那么添加下列一个条件后,能判定≌的是( )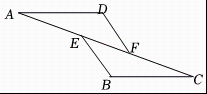 A、 B、 C、 D、3. 如图, , , 则的度数为( )
A、 B、 C、 D、3. 如图, , , 则的度数为( )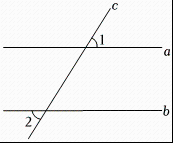 A、 B、 C、 D、4. 如图,直线 , 直线 , 被直线所截,若 , 则的大小为( )
A、 B、 C、 D、4. 如图,直线 , 直线 , 被直线所截,若 , 则的大小为( ) A、 B、 C、 D、5. 如图, , 平分 , 若 , 则的度数为( )
A、 B、 C、 D、5. 如图, , 平分 , 若 , 则的度数为( ) A、 B、 C、 D、6. 下列说法正确的是( )A、如果两个三角形的周长相等,那么这两个三角形一定全等 B、同位角相等 C、在同一平面内经过直线外一点有且只有一条直线与已知直线平行 D、一个角的补角一定是钝角7. 如图,将一块三角尺的直角顶点放在直线a上,a∥b , 则∠2=( )
A、 B、 C、 D、6. 下列说法正确的是( )A、如果两个三角形的周长相等,那么这两个三角形一定全等 B、同位角相等 C、在同一平面内经过直线外一点有且只有一条直线与已知直线平行 D、一个角的补角一定是钝角7. 如图,将一块三角尺的直角顶点放在直线a上,a∥b , 则∠2=( ) A、80° B、70° C、60° D、50°8. 如图,在五边形中, , , , 则的度数是( )
A、80° B、70° C、60° D、50°8. 如图,在五边形中, , , , 则的度数是( ) A、 B、 C、 D、9. 如图, , 平分 , , , , 则下列结论:
A、 B、 C、 D、9. 如图, , 平分 , , , , 则下列结论:
;平分;; .
其中正确结论的个数是( )
A、个 B、个 C、个 D、个10. 如图,把长方形ABCD沿EF折叠后,点D , C'的位置.若∠D'EF=65°,则∠C′FB是( ) A、45° B、50° C、60° D、65°
A、45° B、50° C、60° D、65°二、填空题
-
11. 如图,AB∥CD,DE⊥CE,若∠EDC=40°,则∠AEC= .
 12. 如图, , 点E在上,平分 , 若 , 则的度数为°.
12. 如图, , 点E在上,平分 , 若 , 则的度数为°. 13. 如图,把一个长方形纸片沿折叠后,点D , C分别落在D′,C′的位置,若 , 则等于 .
13. 如图,把一个长方形纸片沿折叠后,点D , C分别落在D′,C′的位置,若 , 则等于 .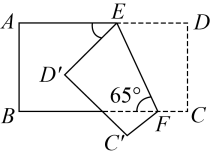 14. 如图,已知直线a//b , 将一块45°含角的直角三角板ABC按如图的方式放置,若∠1=24°,则∠2的度数是 .
14. 如图,已知直线a//b , 将一块45°含角的直角三角板ABC按如图的方式放置,若∠1=24°,则∠2的度数是 . 15. 如图,一个宽度相等的纸条按如图所示方法折叠一下,则
15. 如图,一个宽度相等的纸条按如图所示方法折叠一下,则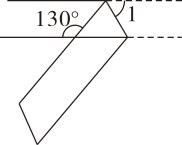
三、解答题
-
16. 已知直线 , 平分且 , , 求的度数.
 17. 如图,四边形中, , , 点 , 分别在 , 上,将沿翻折,得 , 若 , , 求的度数.
17. 如图,四边形中, , , 点 , 分别在 , 上,将沿翻折,得 , 若 , , 求的度数. 18. 如图,已知射线CB∥OA,∠C=∠OAB=100°,点E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
18. 如图,已知射线CB∥OA,∠C=∠OAB=100°,点E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF. (1)、求∠EOB的度数;(2)、若向右平移AB,其他条件都不变,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值.19. 如图,在和中,点、、在一条直线上, , , .求证:.
(1)、求∠EOB的度数;(2)、若向右平移AB,其他条件都不变,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值.19. 如图,在和中,点、、在一条直线上, , , .求证:.
四、综合题
-
20. 如图1,ADBC , ∠BAD的平分线交BC于点G , ∠BCD=90°.
 (1)、如图1,若∠ABG=48°,∠BCD的平分线交AD于点E、交射线GA于点F . 求∠AFC的度数;(2)、如图2,线段AG上有一点P , 满足∠ABP=3∠PBG , 若在直线AG上取一点M , 使∠PBM+∠DAG=90°,求的值.
(1)、如图1,若∠ABG=48°,∠BCD的平分线交AD于点E、交射线GA于点F . 求∠AFC的度数;(2)、如图2,线段AG上有一点P , 满足∠ABP=3∠PBG , 若在直线AG上取一点M , 使∠PBM+∠DAG=90°,求的值.

