（北师大版）2023-2024学年八年级数学上册7.2 定义与命题同步测试

试卷更新日期：2023-10-12 类型：同步测试

进入出卷网下载

一、选择题

1. 下列命题中，真命题的是（）

A、相等的角是对顶角 B、两条直线被第三条直线所截，内错角相等 C、垂直于同一条直线的两条直线互相垂直 D、平行于同一条直线的两条直线互相平行

查看试题解析
2. 下列命题中正确的是（）

A、在同一平面内，过一点有且只有一条直线和已知直线垂直 B、互补的两个角是邻补角 C、在同一平面内，如果 $a ⊥ b$ ， $b ⊥ c$ ，则 $a ⊥ c$ D、两直线平行，同旁内角相等

查看试题解析
3. 下列命题是真命题的是（　　）

A、 $\sqrt{16}$ 的值是 $\pm 4$ B、 $- 64$ 没有立方根 C、 $\frac{22}{7}$ 是有理数 D、实数分为正实数、负实数

查看试题解析
4. 下列命题中是假命题的是（）.

A、同旁内角互补，两直线平行 B、直线 $\vec{a} ⊥ \vec{b}$ ，则a与b相交所成的角为直角 C、如果两个角互补，那么这两个角是一个锐角，一个钝角 D、若 $a ∥ b$ ， $a ⊥ c$ ，那么 $b ⊥ c$

查看试题解析
5. 对于命题“如果 $a^{2} > b^{2}$ ，那么 $a > b$ ”，下面四组关于a，b的值中，能说明这个命题是假命题的是（）

A、 $a = 3$ ， $b = - 2$ B、 $a = - 2$ ， $b = 3$ C、 $a = 3$ ， $b = 2$ D、 $a = - 3$ ， $b = 2$

查看试题解析
6. 能说明命题“一个钝角与一个锐角的差一定是锐角”是假命题的反例是（）

A、 $∠ 1 = 91 ° ， ∠ 2 = 50 °$ B、 $∠ 1 = 89 ° ， ∠ 2 = 1 °$ C、 $∠ 1 = 120 ° ， ∠ 2 = 40 °$ D、 $∠ 1 = 102 ° ， ∠ 2 = 2 °$

查看试题解析
7. 能说明命题“对于任何实数a， $| a | > - a$ ”是假命题的一个反例可以是（）

A、 $a = \sqrt{2}$ B、 $a = \frac{1}{3}$ C、 $a = 1$ D、 $a = - 2$

查看试题解析
8. 如图， $∠ 1 = ∠ 2$ ， $A B ∥ C D$ ， $A B = A C = A E = C D$ ．有下列结论：
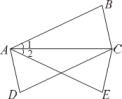
①把 $△ A B C$ 沿直线 $A C$ 翻折180°，可得到 $△ A E C$ ；
②把 $△ A D C$ 沿线段 $A C$ 的垂直平分线翻折180°，可得到 $△ A E C$ ；
③把 $△ A D C$ 沿射线DC方向平移与 $D C$ 相等的长度，可得到 $△ A B C$ ．
其中所有符合题意结论的序号是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
9. 有下列四个命题：①一次函数 $y = - 2 x + 4$ 的函数值随着x值的增大而增大；②等角的补角相等；③如果 $b ∥ a$ ， $c ∥ a$ ，那么 $b ∥ c$ ；④点 $M (- 2 ， 5)$ 关于x轴的对称点是N，则线段 $M N$ 的长是10，其中是真命题的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
10. 下列命题中是真命题的是（）

A、两直线被第三条直线所截，同位角相等 B、对顶角相等 C、若 $a^{2} = b^{2}$ ，则 $a = b$ D、一个数的算术平方根等于它本身，这个数是0

查看试题解析

二、填空题

11. 将命题“对顶角相等”用“如果…那么…”的形式可以改写为．

查看试题解析
12. “对顶角相等”是一个命题（填“真”或“假”）．

查看试题解析
13. 能说明命题：“若两个角 $α$ ， $β$ 互补，则这两个角必为一个锐角一个钝角”是假命题的反例是.

查看试题解析
14. “若 $a b ＞ 0$ ，则 $a ＞ 0$ ， $b ＞ 0$ ”命题（选填“是”或“不是”）．

查看试题解析
15. 在说明命题“若|a|＞3，则a＞3”是假命题的反例中，a的值可以是 .

查看试题解析

三、解答题

16. 证明命题“等腰三角形两腰上的中线相等”。(自己画出图形)
已知：

求证：

证明：

查看试题解析
17. 判断下列命题的真假，若是假命题，请举出反例；若是真命题，请给出证明．
$①$ 若 $a > b$ ，则 $a^{2} > b^{2}$ ；

$②$ 三个角对应相等的两个三角形全等．

查看试题解析
18. 判断下列命题是真命题还是假命题，如果是假命题，请举出一个反例．

(1)、如果一个数是偶数，那么这个数是4的倍数．

(2)、两个负数的差一定是负数．

查看试题解析
19. 如图，直线AB和直线CD，直线BE和直线CF都被直线BC所截．在下面三个条件中，请你选择其中两个作为题设，剩下的一个作为结论，组成一个真命题并证明．
①AB⊥BC，CD⊥BC，②BE∥CF，③∠1＝∠2.

查看试题解析

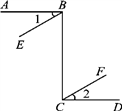
四、综合题

20. 求证：顶角是锐角的等腰三角形腰上的高与底边夹角等于其顶角的一半．

(1)、根据题意补全下图，并根据题设和结论，结合图形，用符号语言补充写出“已知”和“求证”．
已知：在锐角 $△ A B C$ 中， $A B = A C$ ， ▲ ；
求证： ▲ ．

(2)、证明：

查看试题解析
21. 如图，已知四个关系式：①AC＝DC；②BC＝EC；③∠DCA＝∠ECB：④AB＝DE．

(1)、从上面四个关系式中任取三个为条件，余下的一个为结论，组成一个命题．在组成的命题中真命题的个数是；

(2)、从（1）中选择一个真命题进行证明
已知：      ▲ ．
求证：      ▲ ．
证明：      ▲ ．

查看试题解析

（北师大版）2023-2024学年八年级数学上册7.2 定义与命题 同步测试

一、选择题

二、填空题

三、解答题

四、综合题

（北师大版）2023-2024学年八年级数学上册7.2 定义与命题同步测试