（北师大版）2023-2024学年八年级数学上册7.1 为什么要证明同步测试

试卷更新日期：2023-10-12 类型：同步测试

进入出卷网下载

一、选择题

1. 已知 $\sqrt{1} = 1$ ， $\sqrt{1 + 3} = 2$ ， $\sqrt{1 + 3 + 5} = 3$ ， $\sqrt{1 + 3 + 5 + 7} = 4 \dots$ ，依上述规律， $\sqrt{1 + 3 + 5 + 7 + \dots + 2013 + 2015} =$ （）

A、 $2013$ B、 $2015$ C、 $1007$ D、 $1008$

查看试题解析
2. 如图，点 $P$ 是直线 $A B$ 外一点，过点 $P$ 分别作 $C P / / A B$ ， $P D / / A B$ ，则点 $C$ 、 $P$ 、 $D$ 三个点必在同一条直线上，其依据是（）

A、两点确定一条直线 B、同位角相等，两直线平行 C、过直线外一点有且只有一条直线与这条直线平行 D、平行于同一条直线的两条直线平行

查看试题解析
3. 已知整数a₁ ， a₂ ， a₃ ， a₄ ， …满足下列条件：a₁＝0，a₂＝-|a₁+1|．a₃＝-|a₂+2|，a₄＝-|a₃+3|，…依此类推，则a₂₀₂₂的值为（）

A、2022 B、-2022 C、-1011 D、1011

查看试题解析
4. 现有一列数： $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ ， …， $a_{n - 1}$ ， $a_{n}$ （ $n$ 为正整数），规定 $a_{1} = 2$ ， $a_{2} - a_{1} = 4$ ， $a_{3} - a_{2} = 6$ ， …， $a_{n} - a_{n - 1} = 2 n (n \geq 2)$ ，若 $\frac{1}{a_{2}} + \frac{1}{a_{3}} + \frac{1}{a_{4}} \cdot \cdot \cdot \frac{1}{a_{n}} = \frac{97}{198}$ ，则n的值为（）

A、97 B、98 C、99 D、100

查看试题解析
5. 如图，已知 $A B = A_{1} B$ ，在 $A A_{1}$ 的延长线上依次取 $A_{2} 、 A_{3} 、 A_{4} \cdot \cdot \cdot \cdot \cdot \cdot$ ，并依次在三角形的外部作等腰三角形，使 $A_{1} B_{1} = A_{1} A_{2}$ ， $A_{2} B_{2} = A_{2} A_{3}$ ， $A_{3} B_{3} = A_{3} A_{4} \cdot \cdot \cdot \cdot \cdot \cdot$ ，若 $∠ B = 5 0^{∘}$ ，则 $∠ A_{2022} A_{2023} B_{2022}$ 度数为（）

A、 $\frac{5 0^{∘}}{2^{2022}}$ B、 $\frac{5 0^{∘}}{2^{2023}}$ C、 $\frac{6 5^{∘}}{2^{2022}}$ D、 $\frac{6 5^{∘}}{2^{2023}}$

查看试题解析
6. 如图，在平面直角坐标系中， $A_{1} (1 ， - 2)$ ， $A_{2} (2 ， 0)$ ， $A_{3} (3 ， 2)$ ， $A_{4} (4 ， 0)$ ， …根据这个规律，点 $A_{2023}$ 的坐标是（）

A、 $(2022 ， 0)$ B、 $(2023 ， 0)$ C、 $(2023 ， 2)$ D、 $(2023 ， - 2)$

查看试题解析
7. 如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“ $\to$ ”方向排列，如 $(1 ， 0)$ ， $(2 ， 0)$ ， $(2 ， 1)$ ， $(1 ， 1)$ ， $(1 ， 2)$ ， $(2 ， 2)$ ， $⋯$ ，根据这个规律，第 334 个点的坐标为（）

A、 $(8 ， 17)$ B、 $(8 ， 16)$ C、 $(7 ， 17)$ D、 $(7 ， 18)$

查看试题解析
8. $9^{1003} - 7^{902} + 3^{801}$ 的个位数字是（）

A、0 B、3 C、6 D、9

查看试题解析
9. 规定：在平面直角坐标系中，一个点作“0”变换表示将它向右平移一个单位，一个点作“1”变换表示将它关于x轴作对称点，一个点作“2”变换表示将它关于y轴作对称点．由数字0，1，2组成的序列表示一个点按照上面描述依次连续变换．例如：如图，点 $A (- 2 ， 3)$ 按序列“012”作变换，表示点A先向右平移一个单位得到 $A_{1} (- 1 ， 3)$ ，再将 $A_{1} (- 1 ， 3)$ 关于x轴对称得到 $A_{2} (- 1 ， - 3)$ ，再将 $A_{2} (- 1 ， - 3)$ 关于y轴对称得到 $A_{3} (1 ， - 3)$ ．．．．．．依次类推．点 $(1 ， 1)$ 经过“012012012．．．．．．．”100次变换后得到点的坐标为（）．(注：“012”算3次变换)

A、 $(2 ， 1)$ B、 $(- 2 ， - 1)$ C、 $(- 2 ， - 1)$ D、 $(- 1 ， - 1)$

查看试题解析
10. 如图，在平面直角坐标系上有点 $A_{0}$ （1，0），点 $A_{0}$ 第一次跳动至点A（-1，1），第二次点 $A_{1}$ 跳动至点 $A_{2}$ （2，1），第三次点 $A_{2}$ 跳动至点 $A_{3}$ （-2，2），第四次点 $A_{3}$ 跳动至点 $A_{4}$ （3，2），……依此规律跳动下去，则点 $A_{2021}$ 与点 $A_{2022}$ 之间的距离是（）

A、2023 B、2022 C、2021 D、2020

查看试题解析

二、填空题

11. 在 $\sqrt{1}$ ， $\sqrt{2}$ ， $\sqrt{3}$ ， … $\sqrt{2006}$ 中，共有个有理数．

查看试题解析
12. 观察下列等式： $2 + 2^{2} = 2^{3} - 2$ ， $2 + 2^{2} + 2^{3} = 2^{4} - 2$ ， $2 + 2^{2} + 2^{3} + 2^{4} = 2^{5} - 2 \dots$ ，若 $2^{50} = m$ ，则 $2^{101} + 2^{101} + 2^{102} + \dots + 2^{201} =$ $. ($ 用含 $m$ 的代数式表示 $)$

查看试题解析
13. 观察下列等式：2+2²＝2³-2，2+2²+2³＝2⁴-2，2+2²+2³+2⁴＝2⁵-2…，若2⁵⁰＝m ，则2¹⁰¹+2¹⁰¹+2¹⁰²+…+2²⁰¹＝．（用含m的代数式表示）

查看试题解析
14. 在进行二次根式化简时，我们可以将 $\frac{2}{\sqrt{3} + 1}$ 进一步化简，如：
$\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{2 (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}} = \sqrt{3} - 1$

则 $\frac{2}{1 + \sqrt{5}} + \frac{2}{\sqrt{5} + \sqrt{9}} + \frac{2}{\sqrt{9} + \sqrt{13}} + \dots + \frac{2}{\sqrt{4 n - 1} + \sqrt{4 n + 3}}$ ＝.

查看试题解析

三、解答题

15. 求（2-1）（2+1）（2²+1）（2⁴+1）（2⁸+1）…（2³²+1）+1的个位数字．

查看试题解析
16. 阅读下面计算过程：
$\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} - 1$ ；
$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \sqrt{3} - \sqrt{2}$ ；
$\frac{1}{\sqrt{5} + 2} = \frac{1 \times (\sqrt{5} - 2)}{(\sqrt{5} + 2) (\sqrt{5} - 2)} = \sqrt{5} - 2$ ；
请解决下列问题：

(1)、化简： $\frac{1}{\sqrt{3} + 2} =$ ；

(2)、根据上面的规律，请直接写出 $\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ ；

(3)、利用上面的解法，请化简： $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + \dots + \frac{1}{\sqrt{2022} + \sqrt{2023}}$ ．

查看试题解析
17. 如果记 $y = \frac{x^{2}}{1 + x^{2}} = f (x)$ ，并且 $f (1)$ 表示当 $x = 1$ 时y的值，即 $f (1) = \frac{1^{2}}{1 + 1^{2}} = \frac{1}{2}$ ； $f (\frac{1}{2})$ 表示当 $x = \frac{1}{2}$ 时y的值，即 $f (\frac{1}{2}) = \frac{{(\frac{1}{2})}^{2}}{1 + {(\frac{1}{2})}^{2}} = \frac{1}{5}$ ；…，求 $f (1) + f (2) + f (\frac{1}{2}) + f (3) + f (\frac{1}{3}) + ⋯ + f (n) + f (\frac{1}{n})$ 的值（结果用含n的代数式表示）．

查看试题解析

四、综合题

18. 阅读下列材料，然后回答问题．
已知 $a > 0$ ， $S_{1} = \frac{1}{a}$ ， $S_{2} = - S_{1} - 1$ ， $S_{3} = \frac{1}{S_{2}}$ ， $S_{4} = - S_{3} - 1$ ， $S_{5} = \frac{1}{S_{4}}$ ， …．
当n为大于1的奇数时， $S_{n} = \frac{1}{S_{n - 1}}$ ；当n为大于1的偶数时， $S_{n} = - S_{n - 1} - 1$ ．

(1)、求 $S_{3}$ ；（用含a的代数式表示）

(2)、直接写出 $S_{2023} =$ ；（用含a的代数式表示）

(3)、计算： $S_{1} + S_{2} + S_{3} + \cdot \cdot \cdot + S_{2022}$

查看试题解析
19. 在单位长度为1的正方形网格中，如果一个凸多边形的顶点都是网格线交点，我们称其为格点凸多边形，并记该格点多边形的面积为S，多边形内部的格点数为N，多边形边上的格点数为L．

(1)、对于图中的五个凸多边形，补全以下表格：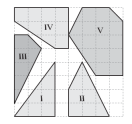
多边形
面积S
内部格点数N
边上格点数L
$N + \frac{L}{2}$
Ⅰ
Ⅱ
7
4
8
8
Ⅲ
Ⅳ
9
5
10
10
Ⅴ
$15.5$
11
11
$16.5$

(2)、借助以上表格猜想格点凸多边形的面积公式：S与 $N + \frac{L}{2}$ 的数量关系可用等式表示为；

(3)、已知格点长方形ABCD，设其边长 $A B = m ， B C = n$ ，其中m，n为正整数．请以格点长方形 $A B C D$ 为例，尝试证明（2）中的格点凸多边形的面积公式．

查看试题解析
20. 一些数按某种规律排列如下：
第一行
1
$\sqrt{2}$
第二行
$\sqrt{3}$
2
$\sqrt{5}$
$\sqrt{6}$
第三行
$\sqrt{7}$
$2 \sqrt{2}$
3
$\sqrt{10}$
$\sqrt{11}$
$2 \sqrt{3}$
第四行
$\sqrt{13}$
$\sqrt{14}$
$\sqrt{15}$
4
$\sqrt{17}$
$3 \sqrt{2}$
$\sqrt{19}$
$2 \sqrt{5}$
……

(1)、根据排列的规律，写出第5行从左数第4个数；

(2)、写出第n（n是正整数）行，从左数第 $n + 1$ 个数（用含n的代数式表示）．

查看试题解析
21. 将分式的分母因式分解后，可以把一个分式表示成两个分式的和或差．观察下列各式，解答下面问题： $\frac{1}{x^{2} + 3 x + 2} = \frac{1}{(x + 1) (x + 2)} = \frac{1}{x + 1} - \frac{1}{x + 2}$
$\frac{1}{x^{2} + 5 x + 6} = \frac{1}{(x + 2) (x + 3)} = \frac{1}{x + 2} - \frac{1}{x + 3}$
$\frac{1}{x^{2} + 7 x + 12} = \frac{1}{(x + 3) (x + 4)} = \frac{1}{x + 3} - \frac{1}{x + 4}$
$\dots$

(1)、； $\frac{1}{x^{2} + x}$ = $\frac{1}{（）}$ - $\frac{1}{（）}$

(2)、计算： $\frac{1}{x^{2} + 4 x + 3} + \frac{1}{x^{2} + 8 x + 15} + \frac{1}{x^{2} + 12 x + 35}$ ．

查看试题解析

多边形	面积S	内部格点数N	边上格点数L	$N + \frac{L}{2}$
Ⅰ
Ⅱ	7	4	8	8
Ⅲ
Ⅳ	9	5	10	10
Ⅴ	$15.5$	11	11	$16.5$

第一行				1	$\sqrt{2}$
第二行			$\sqrt{3}$	2	$\sqrt{5}$	$\sqrt{6}$
第三行		$\sqrt{7}$	$2 \sqrt{2}$	3	$\sqrt{10}$	$\sqrt{11}$	$2 \sqrt{3}$
第四行	$\sqrt{13}$	$\sqrt{14}$	$\sqrt{15}$	4	$\sqrt{17}$	$3 \sqrt{2}$	$\sqrt{19}$	$2 \sqrt{5}$
……

（北师大版）2023-2024学年八年级数学上册7.1 为什么要证明 同步测试

一、选择题

二、填空题

三、解答题

四、综合题

（北师大版）2023-2024学年八年级数学上册7.1 为什么要证明同步测试