(人教版)2023-2024学年九年级数学上册 23.3 课题学习 图案设计 期中专项复习
试卷更新日期:2023-10-11 类型:复习试卷
一、选择题
-
1. 将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 风车应做成中心对称图形,并且不是轴对称图形,才能在风口处平稳旋转.现有一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片,将纸片粘到硬纸板上,做成一个能绕着小孔平稳旋转的风车.正确的粘合方法是( )
2. 风车应做成中心对称图形,并且不是轴对称图形,才能在风口处平稳旋转.现有一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片,将纸片粘到硬纸板上,做成一个能绕着小孔平稳旋转的风车.正确的粘合方法是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 下列每个图中都有一对全等三角形,其中的一个三角形只经过一次旋转运动即可和另一个三角形重合的是( )A、
3. 下列每个图中都有一对全等三角形,其中的一个三角形只经过一次旋转运动即可和另一个三角形重合的是( )A、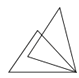 B、
B、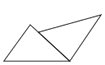 C、
C、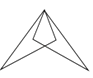 D、
D、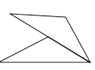 4. 如图所示的各图中可看成由下方图形绕着一个顶点顺时针旋转90°而形成的图形的是( )A、
4. 如图所示的各图中可看成由下方图形绕着一个顶点顺时针旋转90°而形成的图形的是( )A、 B、
B、 C、
C、 D、
D、 5.
5.如图所示,先将图沿着它自己的右边缘翻折,再绕着右下角的一个端点按顺时针方向旋转180°,之后所得到的图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 6. 在以下绿色食品、回收、节能、节水四个标志中,是由某个基本图形经过旋转得到的是( )A、
6. 在以下绿色食品、回收、节能、节水四个标志中,是由某个基本图形经过旋转得到的是( )A、 B、
B、 C、
C、 D、
D、 7.
7.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,使它与图中阴影部分组成的新图形构成中心对称图形,该小正方形的序号是( )
 A、① B、② C、③ D、④8.
A、① B、② C、③ D、④8.下列这些复杂的图案都是在一个图案的基础上,在“几何画板”软件中拖动一点后形成的,它们中每一个图案都可以由一个“基本图案”通过连续旋转得来,旋转的角度正确的是( )
 A、30° B、45° C、60° D、90°9. 如图,经过旋转或轴对称得到 , 其中绕点逆时针旋转的是( )A、
A、30° B、45° C、60° D、90°9. 如图,经过旋转或轴对称得到 , 其中绕点逆时针旋转的是( )A、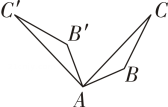 B、
B、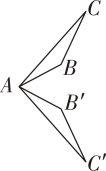 C、
C、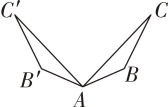 D、
D、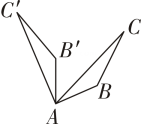 10. 观察下面图案在A、B、C、D四幅图案中,能通过原图案平移得到的是( )
10. 观察下面图案在A、B、C、D四幅图案中,能通过原图案平移得到的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11.
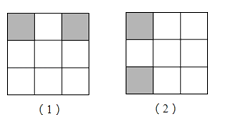
将图(1)中的大正方形绕着其中心顺时针至少旋转 度时,可变成图(2).
 12. 如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的? .
12. 如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的? .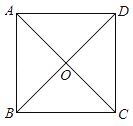 13. 如图,可以看作是一个基础图形绕着中心旋转7次而生成的,则每次旋转的度数是 .
13. 如图,可以看作是一个基础图形绕着中心旋转7次而生成的,则每次旋转的度数是 .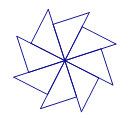 14. 利用图形的旋转可以设计出许多美丽的图案,如图②中的图案是由图①中的基本图形以点O为旋转中心,顺时针旋转4次而生成的,每一次旋转的角度均为α , 则α至少为 .
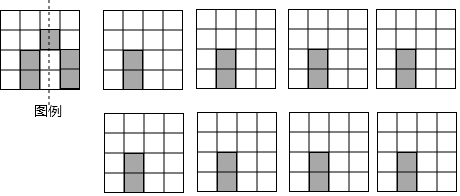
14. 利用图形的旋转可以设计出许多美丽的图案,如图②中的图案是由图①中的基本图形以点O为旋转中心,顺时针旋转4次而生成的,每一次旋转的角度均为α , 则α至少为 .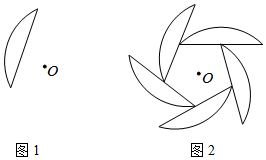 15. 如图“3×3”网格中,有3个涂成黑色的小方格,若再从余下的6个小方格中随机选取1个涂成黑色,则完成的图案为轴对称的概率是 .
15. 如图“3×3”网格中,有3个涂成黑色的小方格,若再从余下的6个小方格中随机选取1个涂成黑色,则完成的图案为轴对称的概率是 .
三、解答题
-
16. 如图,是由4×4个大小完在一样的小正方形组成的方格纸,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)
 17. 在下面16×8的正方形网格中,每个小正方形的边长为1个单位,△ABC是格点三角形(顶点在网格交点处),请你画出:
17. 在下面16×8的正方形网格中,每个小正方形的边长为1个单位,△ABC是格点三角形(顶点在网格交点处),请你画出: (1)、△ABC的中心对称图形,A点为对称中心;(2)、△ABC关于点P的位似△A′B′C′,且位似比为1:2;(3)、以A、B、C、D为顶点的所有格点平行四边形ABCD的顶点D .18. 下图中的四个小三角形都是等边三角形,边长为2 cm,能通过平移△ABC得到其他三角形吗?若能,请画出平移的方向,并说出平移的距离.
(1)、△ABC的中心对称图形,A点为对称中心;(2)、△ABC关于点P的位似△A′B′C′,且位似比为1:2;(3)、以A、B、C、D为顶点的所有格点平行四边形ABCD的顶点D .18. 下图中的四个小三角形都是等边三角形,边长为2 cm,能通过平移△ABC得到其他三角形吗?若能,请画出平移的方向,并说出平移的距离.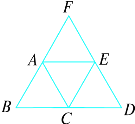 19. 如图,图(1)、图(2)、图(3)、图(4)、图(5)中的图②是由图①经过轴对称,平移,旋转这三种运动变换而得到,请分别指出它们是由其中哪一种运动变换得到的.
19. 如图,图(1)、图(2)、图(3)、图(4)、图(5)中的图②是由图①经过轴对称,平移,旋转这三种运动变换而得到,请分别指出它们是由其中哪一种运动变换得到的.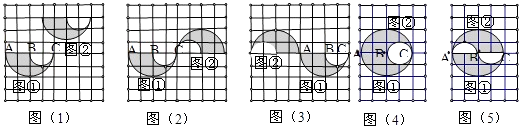
四、综合题
-
20. 认真观察图(1)﹣(4)中的四个图案,回答下列问题:
 (1)、请写出这四个图案都具有的两个共同特征:特征1:;特征2:.(2)、请你在图5中设计出你心中最美的图案,使它也具备你所写出的上述特征.21. 认真观察图(1)﹣(4)中的四个图案,回答下列问题:
(1)、请写出这四个图案都具有的两个共同特征:特征1:;特征2:.(2)、请你在图5中设计出你心中最美的图案,使它也具备你所写出的上述特征.21. 认真观察图(1)﹣(4)中的四个图案,回答下列问题: (1)、请写出这四个图案都具有的两个共同特征:特征1:;特征2:(2)、请你在图5中设计出你心中最美的图案,使它也具备你所写出的上述特征.22. 观察如图①②③中阴影部分构成的图案
(1)、请写出这四个图案都具有的两个共同特征:特征1:;特征2:(2)、请你在图5中设计出你心中最美的图案,使它也具备你所写出的上述特征.22. 观察如图①②③中阴影部分构成的图案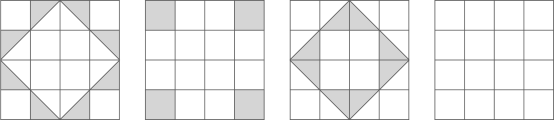
① ② ③ ④
(1)、请你写出这三个图案都具有的两个共同特征:(2)、请在图④中设计一个新的图案,使其满足(1)中的共同特征.23. 如图1,图2,图3的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这个“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题.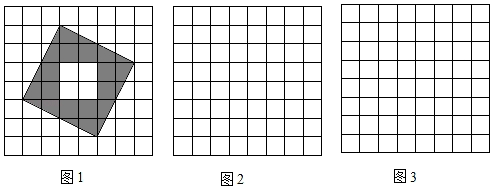 (1)、图1中的“弦图”的四个直角三角形组成的图形是对称图形(填“轴”或“中心”).(2)、请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:
(1)、图1中的“弦图”的四个直角三角形组成的图形是对称图形(填“轴”或“中心”).(2)、请将“弦图”中的四个直角三角形通过你所学过的图形变换,在图2,3的方格纸中设计另外两个不同的图案,画图要求:①每个直角三角形的顶点均在方格纸的格点上,且四个三角形互不重叠,不必涂阴影;
②图2中所设计的图案(不含方格纸)必须是轴对称图形而不是中心对称图形;图3中所设计的图案(不含方格纸)必须既是轴对称图形,又是中心对称图形.